ANSWER - Propagation de la marée dans un estuaire à fond pentu et aux berges convergentes linéaires
Éléments de contexte
English version
Cette page fait partie de la démarche collaborative ANSWER , dont l'objectif est de faire collaborer scientifiques et grand public autour du domaine de l'eau.
Cette fiche fait suite à la fiche "Propagation d'une onde dans un estuaire à pente du fond inclinée" mais traite de la propagation d'une onde dans un estuaire à gabarit rectangulaire dont la section se rétrécie linéairement vers l'amont et dont la pente du fond est également linéaire.
Modélisation mathématique du phénomène de propagation d'une onde dans un estuaire
Nous Partirons du système d'équations de Saint-Venant mono-dimensionnelles, qui auront été linéarisées pour étudier la déformation d'une onde lors de sa propagation le long d'un estuaire schématique.
La linéarisation de ce système va conduire à une équation qui sera résolue directement, fournissant ainsi la variation temporelle de la ligne d'eau et de la vitesse moyenne par section.
Nous étudierons 4 configurations:
- propagation sans frottement avec condition limite amont de sortie libre
- réflexion totale en fond d'estuaire et propagation sans frottement
- propagation avec léger frottement et condition limite amont de sortie libre
- propagation avec fort frottement et condition limite amont de sortie libre
Nous prendrons en compte dans cet exemple un canal de section rectangulaire qui se rétrécie de l'aval (la mer) vers l'amont (la rivière), une pente linéaire constante ascendante vers l'amont et une convergence des berges.
Nous comparerons les résultats obtenus par ces solutions analytiques avec ceux obtenus avec le code de calcul hydrodynamique bidimensionnel aux éléments finis TELEMAC2D.
Hiérarchie des hypothèses simplificatrices
Les simplifications qui suivent nous permettent de développer un modèle linéaire de propagation d'une onde à l'intérieur d'un domaine à géométrie simplifiée, correspondant à un canal avec une pente de fond, qui peut se rapprocher d'un estuaire schématique à l'intérieur duquel se propage une onde de surcote.
Navier-Stokes
- → fluide incompressible
- → intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D
- → accélération négligeable
- → frottement linéarisé
- → accélération négligeable
- → intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D
Expression du modèle simplifié
A partir des hypothèses précédentes, considérons un canal de section en travers rectangulaire et avec pente du fond constante et de taux de convergence des berges constant.
Soit :
- $ h(x,t) $ le niveau d'eau
- $ u(x,t) $ la vitesse moyenne de l'écoulement dans la section de surface $ S(x)=b(x)H(x) $
- $ Q(x,t)=S(x,t)u(x,t) $ le débit à l'abscisse $ x $
- $ b(x)=b_0\dfrac{ x }{ x_0 } $ la largeur du canal qui varie linéairement avec l'abscisse, $ b_0 $ étant la largeur du canal à l'abscisse $ x_0 $ en amont du domaine. $ p_b=b_0/x_0 $
- $ H(x)=H_0\dfrac{ x }{ x_0 } $ la profondeur du canal qui varie linéairement avec l'abscisse. $ p_f=H_0/x_0 $
- $ f $ le coefficient de frottement linéarisé.
Les équations qui régissent le phénomène sont les équations de Saint-Venant 1D linéarisées.
$ \begin{cases} b\dfrac{ \partial h }{ \partial t }+ \dfrac{ \partial Q }{ \partial x }=0 \\ \\ \dfrac{ \partial Q }{ \partial t }+gS \dfrac{ \partial h }{ \partial x }+fQ=0 \end{cases} $
En dérivant la première équation par rapport au temps et la seconde par rapport à l'espace et en éliminant le terme commun, nous obtenons :
$ -b\dfrac{ \partial^2 h }{ \partial t^2 }+ g\dfrac { \partial }{ \partial x }\left[ S\dfrac{ \partial h }{ \partial x }\right]+f\dfrac{ \partial Q }{ \partial x}=0 $
nous allons supposer que $ h $ est de la forme $ h=A(x)e^{-i\sigma t} $. En dérivant, nous obtenons :
$ \dfrac{ \partial h }{ \partial t}=(-i\sigma) A(x) e^{-i\sigma t} = -i\sigma h \qquad et \qquad \dfrac{ \partial^2 h }{ \partial t^2}=-\sigma^2 h $
En reportant ces valeurs dans l'équation ci-dessus :
$ x^2\dfrac{ \partial^2 h }{ \partial x ^2}+2x\dfrac{ \partial h }{ \partial x} + \left[ \sigma (\sigma+fi) \right] \dfrac{ 1}{gp_f} xh=0 $
Posons:
$ k^2=\dfrac{ \sigma^2}{ gH} \text{ le nombre d'onde et }\quad k_f^2=\sigma (\sigma+fi) \dfrac{ x_0}{ gH_0} $
Ce terme est donc une constante.
Par ailleurs, le frottement peut être exprimé de la manière suivante :
$ f=\dfrac{8}{3\pi}\dfrac{g}{K^{2}{H_m^{4/3}}}\left| U_m \right| $
avec :
- $ K $ est le coefficient de Strickler aux alentours de 0.002 - 0.003
- $ H_m $ la profondeur moyenne sur le domaine
- $ U_m $ la vitesse moyennée sur une période sur le domaine
Remarque : cette équation nous montre que la répartition de la hauteur de l'onde est indépendante du taux de convergence linéaire des berges $ p_b $, mais dépend par contre de la hauteur d'eau moyenne $ H_0 $.
Solution analytique
On reconnait une équation de type Bessel:
$ x^2y''+(2p+1) x y'+(\alpha^2x^{2r}+\beta^2)y=0 $
La solution de cette équation est donnée par:
$ y=x^{-p} \left[ c_{1} J_{P/r} (\alpha x^{r}/r) + c_{2} Y_{P/r} (\alpha x^{r}/r) \right] $
Les fonctions $ J_{P/r} $ et $ Y_{P/r} $ sont les fonctions de Bessel respectivement de première et de seconde espèce.
Dans notre cas, nous avons : $ p=1/2, \beta=0, \alpha^2=k_f^2 , r=1/2 $ avec $ P=\sqrt{p^2-\beta^2}=0 $
d'où:
$ h(x)=\dfrac{ 1 } { \sqrt x} \left[ c_{1} J_{1} (2k_f\sqrt x)+c_{2} Y_{1} (2k_f\sqrt x) \right]e^{-i\sigma t} $
L'équation de quantité de mouvement nous permet de calculer la vitesse $ u(x,t): $
$ b\dfrac{ \partial h } { \partial t}+\dfrac{ \partial }{ \partial x} (bHu)=0 $
soit:
$ bHu=i\sigma \dfrac{ b_0 } { x_0}e^{-i\sigma t} \int_{x} \sqrt x \left[ c_{1} J_{1} (2k_f \sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) \right]\, \mathrm dx $
Posons: $ z=2k_f \sqrt x $, il vient : $ dz=k_f \dfrac{1}{\sqrt x} dx $ et $ dx= \dfrac{z}{2k_f^2}dz $
En substituant ces expressions dans l'équation précédente, nous obtenons:
$ bHu= \dfrac{ b_0 } { x_0} \dfrac{ i\sigma} { 4k_f^3} e^{-i\sigma t} \int_{x} z^2 \left[ c_{1} J_{1} (z)+c_{2} Y_{1} (z) \right]\, \mathrm dz $
Pour calculer cette intégrale, nous utilisons la relation de récurrence suivante :
$ \dfrac{d}{dx} (x^n J_{n}(x))=x^n J_{n-1}(x) $, de même pour $ Y_{n}(x) $
Nous obtenons :
$ u=i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x )+c_{2} Y_{2} (2k_f \sqrt x ) \right] e^{-i\sigma t} $
Synthèse : expression de la solution analytique finale
En résumé, l'expression analytique exprimant la variation du niveau d'eau et de la vitesse moyenne en toute section du domaine sont données par les équations suivantes:
$ h(x,t)=\Re \left( \dfrac{ 1} { \sqrt x} \left[ c_{1} J_{1} (2k_f\sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) \right] e^{-i\sigma t}\right) $
$ u(x,t)=\Re \left( i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x) + c_{2} Y_{2} (2k_f \sqrt x) \right] e^{-i\sigma t}\right) $
A partir des expressions générales de $ h(x,t) $ et de $ u(x,t) $, nous pouvons déterminer la solution en fixant 2 conditions aux limites du domaine. Nous allons considérer les deux cas suivants:
- propagation d'une onde incidente à partir de l'aval (droite) vers l'amont du domaine avec condition de sortie libre à l'extrémité amont (gauche)
- réflexion de la même onde incidente à partir de l'aval (droite) vers l'amont avec condition de réflexion totale à l'extrémité amont (gauche)
Configuration n°1 : estuaire sans frottement - sortie libre
Nous allons imposer 2 conditions limites pour déterminer les deux constantes d'intégration.
- une condition limite aval d'entrée de l'onde à l'intérieur du domaine par la droite $ h(x_1,t)=A(x_1,t) e^{-i\sigma t}=a(x_1,t)e^{i(kx_1 -\sigma t)}=a(x_1,t)e^{i\phi} \quad\forall t $
- une condition limite amont de sortie de l'onde sous forme de condition de sortie libre de type Sommerfeld:
$ h(x,t)=a(x_0) e^{i\phi } $
En dérivant cette expression, nous obtenons:
$ \dfrac{ dh }{ dx }=e^{i\phi}\dfrac{ da }{ dx }+iae^{i\phi}\dfrac{ d\phi }{ d x } $
Chaque terme exprime un processus:
- prise en compte du shoaling : $ \dfrac { d a }{ d x }=- \dfrac { 1 }{ 4 } \dfrac { p_0 }{ H } a $. La pente étant nulle, le terme de shoaling s'annule.
- équation eikonale : $ \dfrac{ d\phi }{ d x }=k $($ k $ est le nombre d'onde)
Nous obtenons:
$ \dfrac{ d h }{ d x }= ae^{i\phi}(-\dfrac{1}{4}\dfrac{p_0}{H}+ik) $
ou encore:
$ \dfrac{ d h }{ d x }= A(x,t)e^{-i\sigma t}(-\dfrac{1}{4}\dfrac{p_0}{H}+ik) $
soit:
$ (1) \qquad \dfrac{ d A }{ d x }= A(x,t)(-\dfrac{1}{4}\dfrac{p_0}{H}+ik) $
Or
$ A=\dfrac{1}{\sqrt x}\Big( c_{1} J_{1} (2k_f \sqrt x )+c_{2} Y_{1} (2k_f \sqrt x ) \Big) $
En dérivant cette expression, nous obtenons:
$ (2) \qquad \dfrac{dA}{dx}=-\dfrac{1}{2}\dfrac{1}{x\sqrt x }\Big[c_{1} J_{1} (2k_f \sqrt x )+c_{2} Y_{1} (2k_f \sqrt x ) \Big] - \dfrac{k_f}{x} \Big[ c_{1} J_{2} (2k_f \sqrt x )+c_{2} Y_{2} (2k_f \sqrt x ) \Big] $
sachant que :
$ \dfrac {d } {dz} J_{1}(z) =- J_{2} (z)\quad \text{et}\quad \dfrac {d } {dz} Y_{1}(z) =- Y_{2} (z) $
En applicant la relation (2) en $ x=x_0 $ et en posant :
$ \gamma =-\dfrac{1}{2 }-ikx_0 \qquad\text {et} \qquad \delta=-k_f \sqrt x_0 $
Nous obtenons le système suivant à résoudre pour calculer les coefficients :$ c_{1} \text {et} c_{2} $
$ \begin{cases} c_{1} ( \gamma J_{1}^0 + \delta J_{2}^0 )+ c_{2}( \gamma Y_{1}^0 + \delta Y_{2}^0 )=0 \\ \\ c_{1}J_{1}^1 +c_{2}Y_{1}^1 =A_1 \sqrt x_1 \end{cases} $
Ceci conduit à la solution suivante :
$ \begin{cases} D=( \gamma J_{1}^0 + \delta J_{2}^0 ) Y_{1}^1 - ( \gamma Y_{1}^0 + \delta Y_{2}^0 )J_{1}^1 \\ D_{c_1}=-A_1\sqrt {x_1}( \gamma Y_{1}^0 + \delta Y_{2}^0 ) \\ D_{c_2}=A_1\sqrt {x_1} ( \gamma J_{1}^0 + \delta J_{2}^0 ) \\ c_1=D_{c_1}/D \qquad c_2=D_{c_2}/D \\ h(x,t)=\Re \left( \dfrac{ 1} { \sqrt x} [ c_{1} J_{1} (2k_f \sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) ] e^{-i\sigma t}\right) \\ u(x,t)=\Re \left( i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x) + c_{2} Y_{2} (2k_f \sqrt x) \right] e^{-i\sigma t}\right) \end{cases} $
Cas d'application : translation d'une onde sinusoïdale
Les caractéristiques de cet exemple sont les suivantes:
- longueur du canal : 10 000 km
- période de la marée : 900s
- amplitude : 1 m à l'amont
- pente du fond : 0,0001 m/m
- profondeur à l'entrée du canal à l'aval : 100 m et à sa sortie amont : 20 m
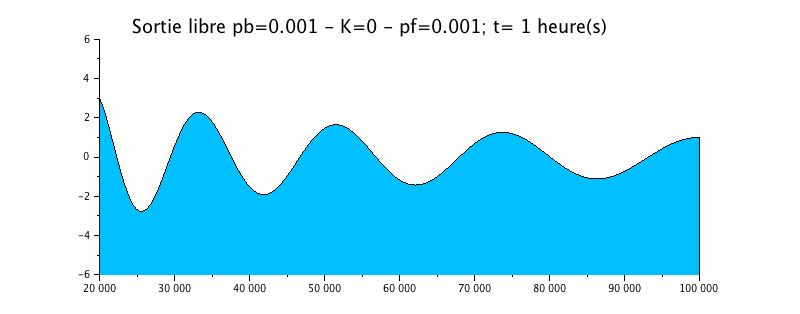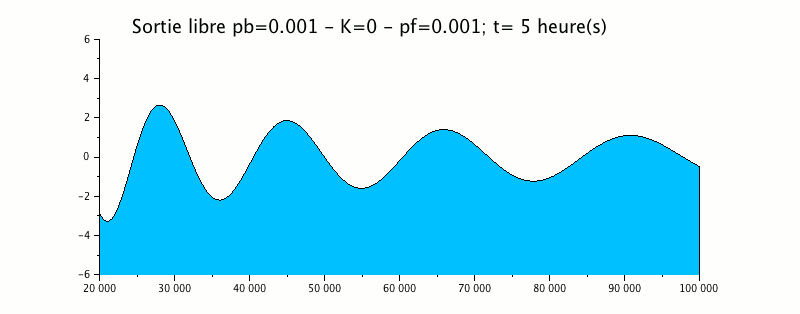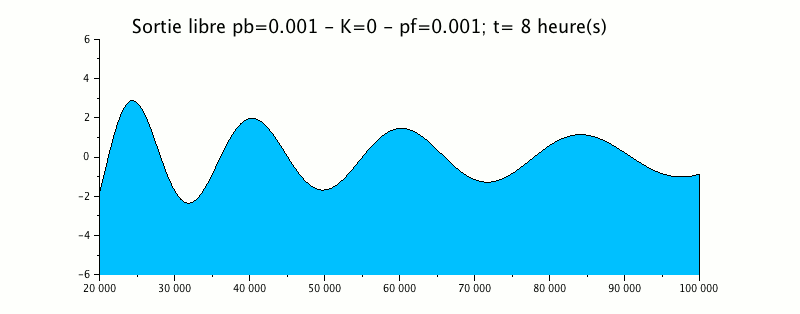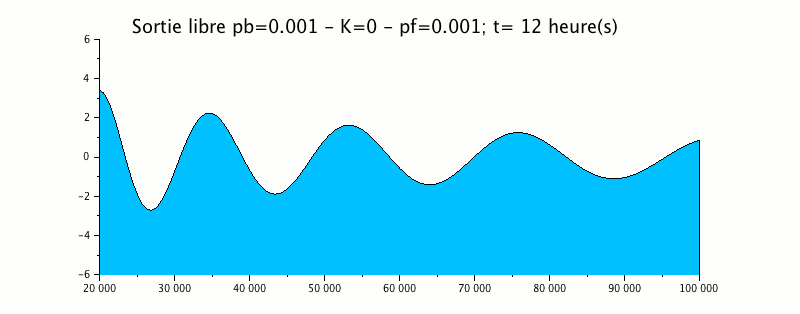
L'animation suivante représente la propagation d'une onde de marée de 12 heures dans un estuaire dont le fond remonte linéairement et les berges convergent linéairement.
|

|
Cet exemple montre que l'onde générée à l'aval (droite sur le schéma) avec une amplitude de 1m se propage vers l'amont (gauche) en se déformant : diminution de la longueur d'onde, augmentation de l'amplitude.
A l'extrémité gauche, cette onde sort du domaine sans générer d'onde de réflexion, ce qui valide la condition de sortie libre utilisée ici.
Le terme de shoaling introduit est d'un ordre de grandeur inférieur au terme eikonale et ne produit aucune modification sensible à la sortie de l'onde.
Par ailleurs, la courbe enveloppe montre clairement une amplification du signal vers l'amont.
Comparaison avec le code de calcul TELEMAC2D
Configuration n°2 : estuaire sans frottement - réflexion d'une onde à l'intérieur du domaine / berges et fond linéaires
Introduisons les conditions limites suivantes, qui correspondent à :
- une condition limite aval d'entrée de l'onde à l'intérieur du domaine par la droite $ h(x_1,t)=A_1(x_1,t) e^{-i\sigma t}\quad\forall t $
- une condition limité amont de réflexion totale de l'onde $ u(x)=0 \quad\forall t $
Nous aboutissons au système suivant :
$ \begin{cases} c_1 J_{2}^0+c_2 Y_{2}^0 =0 \\ \\ c_1 J_{1}^1+c_2 Y_{1}^1 =A_1 \sqrt {x_1} \end{cases} $
Dont la résolution conduit à:
$ \begin{cases} D= J_{2}^0 Y_{1}^1 - J_{1}^1 Y_{2}^0 \\ D_{c_1}=-A_1\sqrt x_1 Y_{2}^0 \\ D_{c_2}=A_1\sqrt x_1 J_{2}^0 \\ c_1=D_{c_1}/D \qquad c_2=D_{c_2}/D \\ h(x,t)=\Re \left( \dfrac{1} { \sqrt x} \left[ c_{1} J_{1} (2k_f \sqrt x)+c_{2} Y_{1} (2k_f \sqrt x) \right] e^{-i\sigma t}\right) \\ u(x,t)=\Re \left( i\sigma \dfrac{ 1} { k_f} \dfrac{x_0} { H_0} \dfrac{1} { x} \left[ c_{1} J_{2} (2k_f \sqrt x) + c_{2} Y_{2} (2k_f \sqrt x) \right] e^{-i\sigma t}\right) \end{cases} $
On vérifie bien que $ h(x_1,t) = A_1 e^{-i\sigma t} $
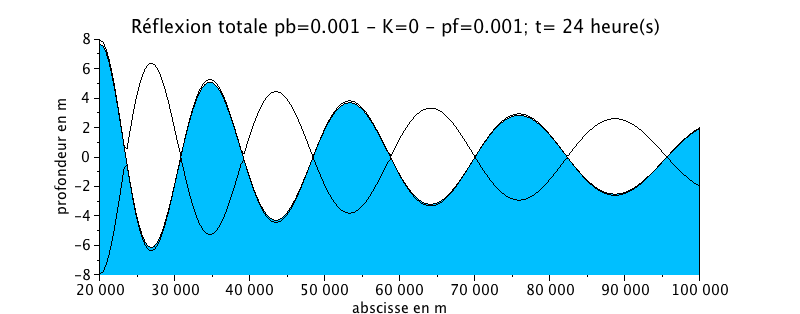
Cas d'application : réflexion d'une onde sinusoïdale
Le même cas que ci-dessus est utilisé, mais en imposant une condition limite de réflexion à l'amont. Dans ce cas, une onde réfléchie de même période, de même amplitude mais de sens de propagation opposée vient se superposer à l'onde incidente. Ceci conduit donc au niveau de la frontière "mer" (de droite), à imposer 2 fois l'amplitude de l'onde incidente à la frontière "mer".
[[ ]] ]]
|
|
Cette animation montre la formation de ventres et de creux réguliers ce qui représente une réflexion totale.
La longueur d'onde diminue de manière progressive vers l'amont en fonction de la hauteur d'eau. On note également une augmentation de l'amplitude des battements vers l'amont.
Ainsi, en l'absence de tout frottement, l'onde se propage sans perte d'énergie sous l'effet de la contraction des berges et de la pente du fond (à comparer avec le cas similaire sans pente où l'on n'observe aucune déformation).
Comparaison avec le code de calcul TELEMAC2D
Propagation d'une onde dans un estuaire à pente... par Wikhydro
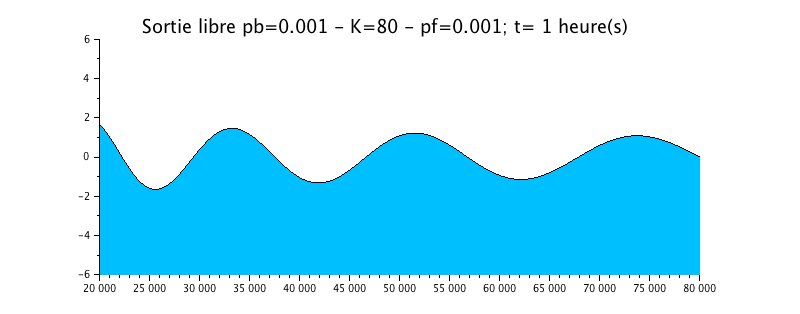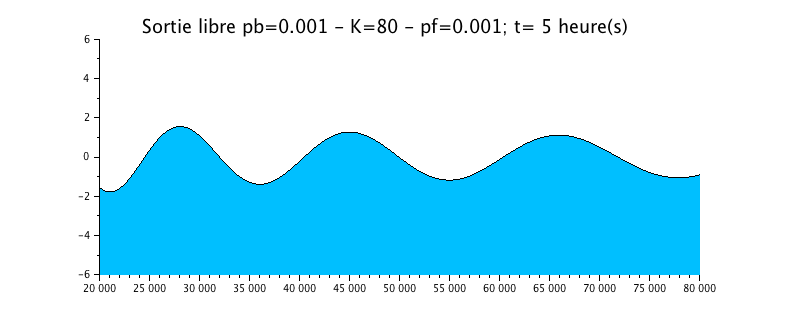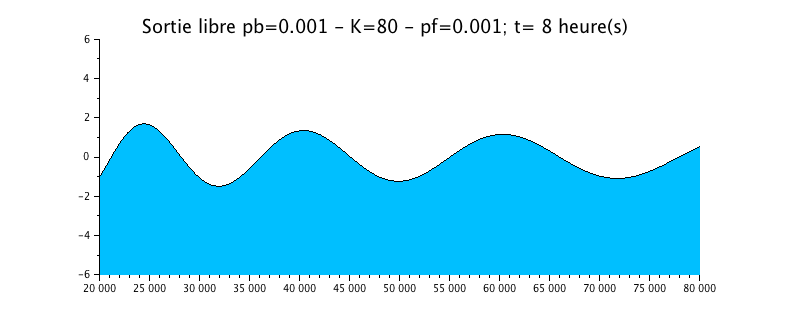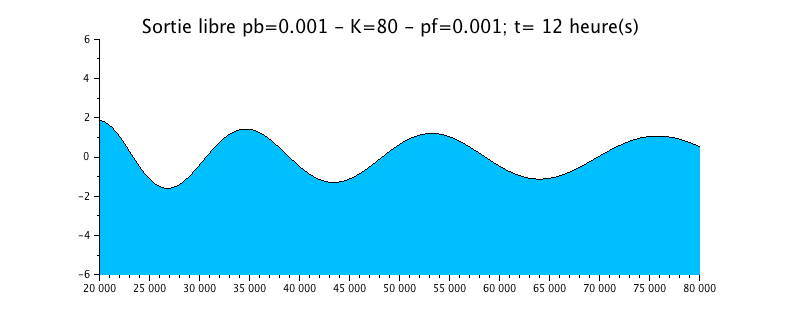
Configuration n°3 : Estuaire HYPERSYNCHRONE avec frottement / K=80
Nous avons repris le cas précédent de la propagation de l'onde avec une sortie libre, mais nous lui avons rajouté un peu de frottement sous la forme d'un coefficient de Strickler de 50.
|

|
L'animation montre un effet certain mais de faible amplitude sur l'évolution du niveau d'eau. Celui-ci est tout de même légèrement amorti par rapport à la solution sans frottement (configuration n°1).
La courbe enveloppe montre l'effet d'amplification du signal vers l'amont (gauche)
Comparaison avec TELEMAC 2D
Configuration n°4 : Estuaire HYPOSYNCHRONE avec frottement / K=50
Nous avons repris le cas précédent de la propagation de l'onde avec une sortie libre, mais nous lui avons rajouté un peu plus de frottement sous la forme d'un coefficient de Strickler de 50.
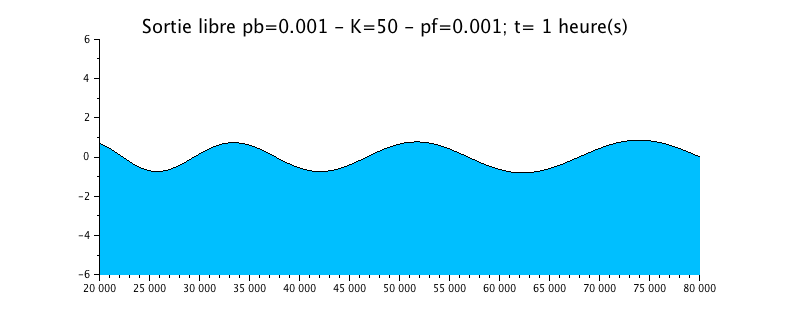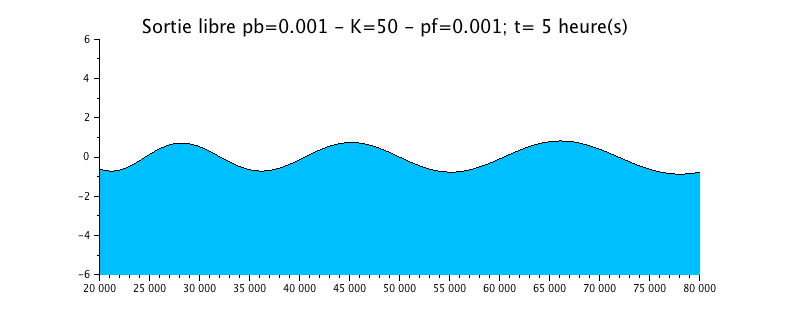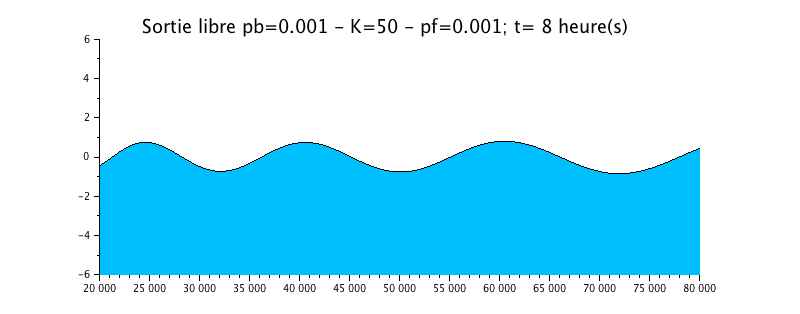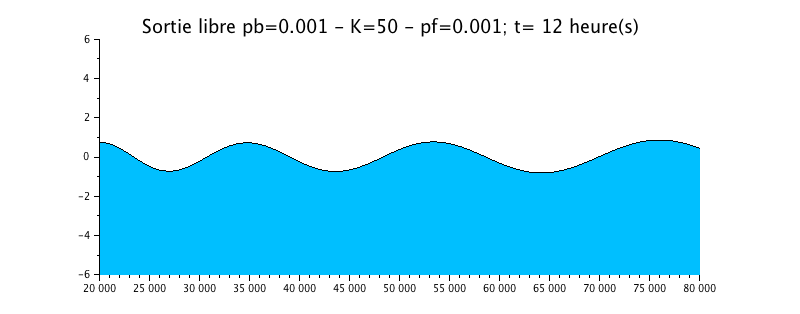
|
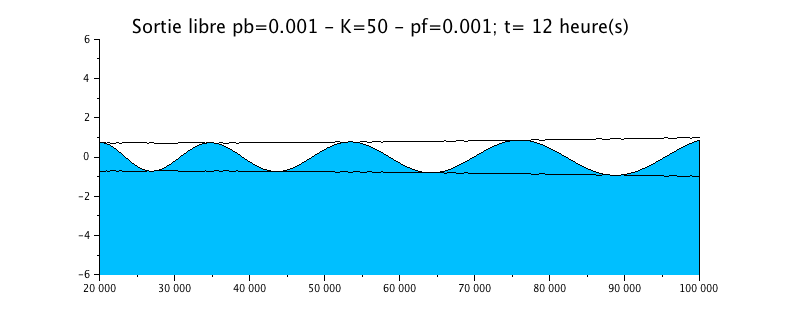
|
L'animation montre un effet certain, plus important que dans le cas précédent sur l'évolution du niveau d'eau. Celui-ci est beaucoup plus amorti par rapport à la solution sans frottement (configuration n°1).
La courbe enveloppe montre une nette atténuation du signal vers l'amont, ce qui rend l'estuaire hyposynchrone.
Comparaison avec le code de calcul TELEMAC2D
Conclusion générale sur la simulation de la propagation d'une onde dans un estuaire à pente du fond constante et à section constante
Les travaux qui ont été à l'origine de ce papier ont permis de dériver les équations susceptibles de représenter l'entrée d'une onde dans un estuaire caractérisé par un fond en pente linéarisée ascendant vers l'amont et un gabarit dont les berges convergent linéairement également vers l'amont.
Plusieurs enseignements peuvent être tirées de ces résultats:
- les conditions limites de sortie libre de Sommerfeld donnent toutes satisfactions : l'on sort sans générer en interne du domaine des ondes de réflexion
- la condition de réflexion totale imposée en fond d'estuaire représente donc bien le phénomène par la solution analytique. Par contre, l'utilisation du code numérique génère également une onde de réflexion à l'intérieur du domaine qui vient se superposer à la condition limite amont et nuit à la restitution correcte, allant même jusqu'à faire exploser le modèle. Un remarque est ici nécessaire sur ce que l'on représente exactement avec la solution limite. Si l'on veut représenter la superposition de l'onde incidente et de l'onde réfléchie, il faut doubler l'onde à la condition limite. Ainsi, on voit ici que l'enrichissement des 2 méthodes est réciproque.
- la prise en compte d'un frottement est également fort instructif. Tout d'abord, il faut rappeler que sans frottement, l'estuaire est HYPERSYNCHRONE, du fait de sa pente ascendante et de son gabarit rétréci. Si l'on rajoute un peut de frottement (K=80), l'onde diminue, ce qui est bien conforme à la théorie.Par contre, si le frottement augmente, le train d'onde est beaucoup plus écrasé en amplitude, amenant même l'estuaire à devenir HYPOSYNCHRONE.
Bibliographie
- Le Méhauté B., "An Introduction to Hydrodynamics & Waterways" Springer-Verlag, 1976, 315 p.
- Thual O., "Hydrodynamique de l'environnement", Les éditions de l'Ecole Polytechnique, Oct. 2011, 314 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 1 - Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 471 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 2 - Non-Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 494 p.
- Tanguy J.M. "Traité d'hydraulique environnementale", vol.2, "processus maritimes", reps. publi. JM Tanguy, Ed. Hermès - Lavoisier, 2010.
- site du SHOM et plus particulièrement une page dédiée aux courants de marée
- D. Prandle and M. Rahman, "Tidal Respo,se in Estuaries" Journal of the Physical Oceanography, Vol. 10, pp 1552 - 1573, 1980
Code Scilab
Les animations précédentes ont été réalisées à l'aide le l'application SCILAB.
Elles peuvent être utilisées pour reproduire le graphique. Il suffit de sélectionner l'ensemble du texte dans le fichier *.pdf et de le copier dans l'éditeur du logiciel puis d'exécuter le programme.
Le fichier est disponible ici : Fichier:Estuaire avec correction.pdf fournit le code SCILAB du programme qui fournit les animations précédentes.
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS
