ANSWER : ondes de disjonction dans les canaux : Différence entre versions
(→Ondes négative : onde de rupture d'un barrage) |
(→Rappel de la théorie de Stoker) |
||
| Ligne 272 : | Ligne 272 : | ||
Les essais CNR n'ont pas été réalisés strictement dans les conditions idéales de la théorie de Ritter : la canal a été utilisé avec une pente du fond et une ligne d'eau se rapprochant du régime normal d'écoulement. Les vitesses de propagation du front sec mesurées dans les différents essais sont répertoriées dans le tableau ci-dessous. | Les essais CNR n'ont pas été réalisés strictement dans les conditions idéales de la théorie de Ritter : la canal a été utilisé avec une pente du fond et une ligne d'eau se rapprochant du régime normal d'écoulement. Les vitesses de propagation du front sec mesurées dans les différents essais sont répertoriées dans le tableau ci-dessous. | ||
| − | === | + | === Théorie de Stoker=== |
Stoker (1957) compléta la théorie de Ritter en traitant des configurations plus complètes, toujours par la théorie des caractéristiques. Nous nous intéresserons ici à la prise en compte d'une lame d'eau à l'aval du barrage. | Stoker (1957) compléta la théorie de Ritter en traitant des configurations plus complètes, toujours par la théorie des caractéristiques. Nous nous intéresserons ici à la prise en compte d'une lame d'eau à l'aval du barrage. | ||
| + | |||
| Ligne 289 : | Ligne 290 : | ||
Soit : <math>C_{tc})(h_2-h_0)=U_2h_2</math><br /> | Soit : <math>C_{tc})(h_2-h_0)=U_2h_2</math><br /> | ||
L'introduction de la valeur de la vitesse de l'onde négative d'aval : <math>U(h)=-2\sqrt{gh_2}+2\sqrt{gh_1}</math> , nous donne:<br /> | L'introduction de la valeur de la vitesse de l'onde négative d'aval : <math>U(h)=-2\sqrt{gh_2}+2\sqrt{gh_1}</math> , nous donne:<br /> | ||
| − | <math>C_{tc}=\dfrac{ -2\sqrt{gh_2}+2\sqrt{gh_1} }{ h_2-h_0 } </math><br /> | + | <math>C_{tc}=\dfrac{ (-2\sqrt{gh_2}+2\sqrt{gh_1})h_2 }{ h_2-h_0 } </math><br /> |
Par ailleurs, nous avions vu que la relation de continuité nous a permis d'obtenir:<br /> | Par ailleurs, nous avions vu que la relation de continuité nous a permis d'obtenir:<br /> | ||
<math>C_{tc}=\sqrt{gh_0}\sqrt{\dfrac{h_2}{ 2h_0} (1+\dfrac{h_2}{ h_0})}} </math><br /> | <math>C_{tc}=\sqrt{gh_0}\sqrt{\dfrac{h_2}{ 2h_0} (1+\dfrac{h_2}{ h_0})}} </math><br /> | ||
Version du 3 janvier 2017 à 11:31
Sommaire |
Eléments de contexte
Cette fiche a été conçue dans le cadre du projet de sciences participatives ANSWER qui a pour objectif de rassembler ou de développer suivant l'état des connaissances, des solutions analytiques des équations de Navier-Stokes dans les domaines de l'hydraulique à surface libre. Il s'agit de les valider par des essais en laboratoire et de les comparer avec des codes de calcul sur des cas schématiques. Des vidéos illustrent ces processus dans la nature si cela s'avère techniquement réalisable.
Problématique
Le problème de la rupture de barrage a été étudié par Ritter à la fin du 19ème siècle qui a signé la publication de sa théorie [1] dans le cas simplifié d'un canal à fond plat en supposant un effacement instantanée du barrage et en négligeant tout frottement sur les parois et le fond du lit du canal. De plus, l'aval du canal était supposé sec.
En 1951, Stoker [2] repris le problème en étudiant des cas plus complexes et plus réalistes en prenant en compte la pente du canal, la présence d'une lame d'eau à l'aval du barrage puis du frottement sur le fond.
Whitman a proposé en 1954 une méthode approchée pour calculer l'effet du frottement sur le fond, ce qui a permis d'obtenir une ligne d'eau plus conforme à la réalité.
Des développements assez récents ont encore été réalisés pour améliorer la précision des résultats (Hogg & Pritchard, 2004; Ancey et al. 2006 et 2007).
Les essais que nous avons réalisés à la CNR en octobre 2016 ont permis la constitution d'une base de données comprenant plusieurs essais où le niveau d'eau amont, le niveau d'eau aval, le débit et la pente du fond ont été modifiés.
Afin de tester les diverses théories et les comparer à nos résultats obtenus sur le canal expérimental, nous allons les confronter aux théories de Ritter et de Stoker. Pour présenter ces 2 théories, nous utiliserons la présentation de Graf et Altinakar [3]
Mise en équations
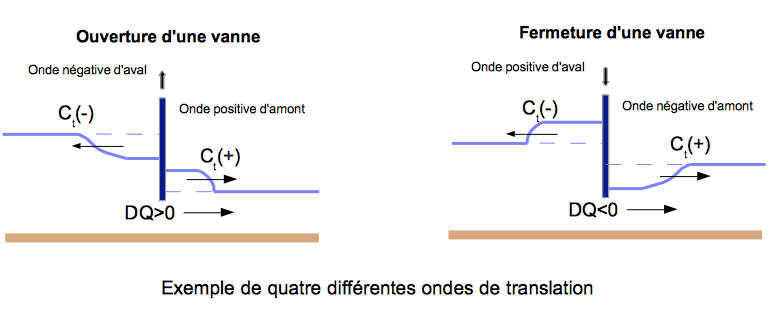
Nous nous placerons ici dans des configurations de fermetures ou d'ouvertures de vannes, qui vont provoquer de brusques variations et la génération d'ondes que nous appellerons ondes de disjonction ou de translation. L'écoulement sera supposé non stationnaire et rapidement varié. Nous distinguerons quatre différents types d'onde qui résultent de deux situations :
- la fermeture d'une vanne produit :
- une onde positive vers l'amont (blocage du débit) qui provient donc de l'aval (appelée onde positive d'aval)
- une onde négative vers l'aval (baisse de niveau dû à une diminution de débit) qui provient donc de l'amont (appelée onde négative d'amont)
- l'ouverture d'une vanne produit:
- une onde négative vers l'amont (augmentation du débit à l'aval) qui provient donc de l'aval (appelée onde négative d'aval)
- une onde positive vers l'aval (augmentation de débit) qui provient donc de l'amont (appelée onde positive d'amont)
Nous reprendrons ici les appellations et les développements de W.H. Graf et M.S. Altinakar (1)
La figure suivante représente les 4 ondes de disjonction (ou de translation)
En ce qui concerne le type de modélisation qui pourrait représenter les 4 ondes, il convient de remarquer que :
- les ondes positives d'amont ou d'aval constituent une surélévation par rapport au plan d'eau initial. Le niveau de la discontinuité de la ligne d'eau supérieure se propage avec une profondeur supérieure au niveau inférieur de la discontinuité. L'onde déferle donc rapidement, sous forme d'un ressaut qui se propage à haute vitesse. Il se produit d'ailleurs un cisaillement dans la colonne liquide. Cette onde positive ne peut donc se modéliser par un modèle de Saint-Venant.
- les ondes négatives par contre sont des ondes de détente puisque le niveau supérieur de l'onde correspondant à la surface libre se déplace plus vite que le niveau inférieur. Ces ondes peuvent donc se modéliser avec des modèles de Saint-Venant.
Ondes positives
Equation de continuité
Considérons un volume unité de fluide. L'équation de continuité traduit la conservation du fluide le long d'un tube de courant $ x $ qui traverse avec un débit $ Q $ une surface $ S $. Elle s'écrit:
$ \dfrac{ \partial S }{ \partial t }+\dfrac{ \partial Q }{ \partial x }=0 $
Or le premier membre peut être transformé en :
$ \dfrac{ \partial S }{ \partial t }=\dfrac{ \partial S}{ \partial Q }\dfrac{ \partial Q}{ \partial t } $
L'équation de continuité s'écrit alors:
$ \dfrac{ \partial S }{ \partial Q}\dfrac{ \partial Q}{ \partial t }+\dfrac{ \partial Q}{ \partial x }=0 $
Ou encore:
$ \dfrac{ \partial Q }{ \partial t}+\dfrac{ \partial Q}{ \partial S }\dfrac{ \partial Q}{ \partial x }=0 $
Ce qui revient à dire que le débit $ Q $ est constant le long de la caractéristique et qu'il se déplace à la vitesse suivante :
$ c=\dfrac{ \partial Q }{ \partial S} $
qui est la célérité de l'onde transportant le débit $ Q $:
L'équation de continuité s'écrit alors:
$ \dfrac{\partial Q }{ \partial t }+c\dfrac{ \partial Q }{ \partial x }=0 $
Equation de quantité de mouvement
La première loi de Newton nous permet d'écrire que la variation de quantité de mouvement d'un corps de masse $ m $ occupant un volume de contrôle $ V $ est le résultat de la somme des forces qui lui sont appliquées. Ainsi:
$ \sum\vec{ F_e}= \int_{m} \dfrac{ d(m\vec{U}) }{ d t } =\int_{V} \rho\dfrac{ d\vec{U} }{ d t } \mathrm{d}V $
Nous supposons que l'axe des $ x $ est perpendiculaire à la surface $ S $. Si le fluide ne se déplace que selon la direction $ x $, nous pouvons écrire:
$ \dfrac{ dU}{ dt } = \dfrac{ \partial U}{ \partial t } +U\dfrac{ \partial U}{ \partial x} $
Soit :
$ \sum {F_e}= \int_{V} \ro\dfrac{ \partial U }{ \partial t } \mathrm{d}V + \int_{V} \ro U\dfrac{ \partial U }{ \partial x} \mathrm{d}V $
Traitons ces deux membres en décomposant la direction $ x $ et la surface $ S $ :
$ \sum {F_e}=\sum {F_{e1}}+\sum {F_{e2}} $
première partie
$ \sum {F_{e1}}= \int_{V} \rho \dfrac{ \partial U }{ \partial t} \mathrm{d}V $
qui peut se décomposer suivant la direction $ x $ et la surface $ S $
$ \sum {F_{e1}}= \rho \int_{x} \int_{S} \dfrac{ \partial U }{ \partial t} \mathrm{d}x \mathrm{d}S $
Ce qui conduit à:
$ \sum {F_{e1}}= \rho \int_{x} \dfrac{ \partial Q }{ \partial t} \mathrm{d}x $
En utilisant l'équation de continuité, nous obtenons entre deux sections;
$ \sum {F_{e1}}= -\rho c\int_{x} \dfrac{ \partial Q }{ \partial x} \mathrm{d}x $
Soit en intégrant suivant la direction $ S $ :
$ \sum {F_{e1}}= -\rho c \Delta Q $
seconde partie
$ \sum {F_{e2}}= \int_{x} \int_{S} \ro U\dfrac{ \partial U }{ \partial x} \mathrm{d}x \mathrm{d}S $
Nous obtenons:
$ \sum {F_{e2}}= \rho \int_{x} \dfrac{ \partial U }{ \partial x} \mathrm{d}x \int_{S} U\mathrm{d}S $
Or la seconde partie de l'intégrale représente le débit traversant la surface $ S $ :
L'équation de continuité s'écrit donc:
$ \sum {F_{e2}}= -\rho c \Delta U Q $
expression générale de l'équation de continuité
$ \sum {F_{e}}= \rho Q \Delta U- \rho c \Delta Q $
Application à un canal
Soit un canal rectiligne de gabarit constant. Ecrivons le système d'équations (continuité et quantité de mouvement) entre 2 sections $ S_1 $ et $ S_2 $ caractérisées par des vitesses de l'écoulement $ U_1 $ et $ U_2 $ .
$ \begin{cases} (U_1-c)S_1=(U_2-c)S_2 \\ \sum {F_{e}}= \rho \left[ Q_2U_2-Q_1U_1-c (Q_2-Q_1) \right] \end{cases} $
En réarrangeant et en utilisant l'équation de continuité, nous obtenons:
$ \begin{cases} (U_1-c)S_1=(U_2-c)S_2 \\ \sum {F_{e}}= \rho \left[ (U_2-U_1)(U_1-c) S_1 \right] \end{cases} $
Nous allons maintenant exprimer les forces extérieures pour un canal de gabarit constant et de pente négligeable et de très faible rugosité. Seule est donc prise en compte les forces de pression qui s'exercent selon les deux surfaces de profondeur $ h_1 $ et $ h_2 $ et de largeur $ B $
$ \sum {F_{e}}= -\rho g \int_{x} S \dfrac{ \partial h }{ \partial x} \mathrm{d}x =-\rho g \int_{x} Bh \dfrac{ \partial h }{ \partial x} \mathrm{d}x=-\rho g B\int_{x} S \dfrac{ 1}{ 2} \dfrac{ \partial h^2 }{ \partial x} \mathrm{d}x $
D'où finalement:
$ \sum {F_{e}}= g\dfrac{ h_1^2 }{ 2}-g\dfrac{ h_2^2 }{ 2} $
Finalement nous obtenons :
$ g\dfrac{ h_1^2 }{ 2}-g\dfrac{ h_2^2 }{ 2}=h_1(U_1-c)(U_2-U_1) $
et donc l'expression de la célérité de l'onde:
$ c=U_1-\sqrt {gh_1} \sqrt { \dfrac {h_2 }{ 2h_1} \left( 1+\dfrac { h_2 }{ h_1} \right) } $
Pour résoudre ce problème, nous connaissons en général $ h_1 $, $ U_1 $ et la variation de débit $ \Delta Q $.
En utilisant cette dernière relation et la valeur de la célérité : $ c=\Delta Q/\Delta S =\Delta q/\Delta h $, nous pouvons en déduire $ h_2 $ et $ c $.
A noter que l'expression ci-dessus est valable pour les ondes d'aval positives et négatives. Pour les ondes d'amont positives et négatives, il convient de prendre un signe positif avant le radical dans l'expression ci-dessus.
Ondes négative : onde de rupture d'un barrage
Nous allons déterminer dans ce cas simple, le profil de l'onde de rupture d'un barrage en utilisant successivement les théories de Ritter [1] et de Stoker [2]
Théorie de Ritter
Cette théorie suppose un effacement immédiat du barrage dans un canal de section constante, sans pente et sans frottement. Cette théorie prend appui sur la théorie des caractéristiques, remarquablement formulée par Courant et Friedrichs [4]. Elle consiste à partie des équations de SaintVenant 1D:
$ \begin{cases} \dfrac{ \partial u }{ \partial t }+u\dfrac{ \partial u }{ \partial x }+g\dfrac{ \partial \eta }{ \partial x }=0<br /> \\\\ \dfrac{ \partial \eta }{ \partial t }+\dfrac{ \partial (h+\eta)}{ \partial x }=0 \end{cases} $
En opérant le changement de variable $ c=sqrt(g(h+\eta)) $, nous obtenons:
$ \begin{cases} \dfrac{ \partial u }{ \partial t }+u\dfrac{ \partial u }{ \partial x }+2c\dfrac{ \partial c }{ \partial x }=0<br /> \\\\ \dfrac{ 2\partial c }{ \partial t }+2u\dfrac{ \partial c}{ \partial x }+c \dfrac{ \partial u}{ \partial x }=0 \end{cases} $
En faisant respectivement la somme et la différence de ces 2 équations, nous obtenons:
$ \begin{cases} \left [ \dfrac{ \partial }{ \partial t }+(u+c)\dfrac{ \partial }{ \partial x } \right](u+2c)=0<br /> \\\\ \left [ \dfrac{ \partial }{ \partial t }+(u-c)\dfrac{ \partial }{ \partial x } \right](u-2c)=0<br /> \end{cases} $
Ces 2 relations représentent les équations de deux courbes caractéristiques $ C^+ $ et $ C^- $, de pentes:
$ \begin{cases} \dfrac{ dx }{ dt }=u+2c<br /> \\\\ \dfrac{ dx }{ dt }=u-2c<br /> \end{cases} $
le long desquelles la quantité $ u+2c $ est constante sur $ C^+ $ et la quantité $ u-2c $ est constante sur $ C^- $. Ceci signifie que l'une ou l'autre des ces 2 invariants $ u\pm 2c $ est constant pour un point se déplaçant au sein du fluide avec la vitesse $ u\pm c $.
Nous allons appliquer cette théorie au problème de la rupture d'un barrage, dont la surface libre est représentée à différents pas de temps sur la figure c-dessous:
Lorsque le barrage disparait instantanément, il se produit une onde de détente qui se déplace à la fois vers l'aval sur fond sec et vers l'amont. Dans l'espace (x,t), 3 zones différentes apparaissent:
- Zone I : Cette zone n'est pas impactée par la remontée de l'onde vers l'amont. C'est une zone de calme
- Zone III : Cette zone n'est pas impactée par la propagation de l'onde de détente vers l'aval. C'est une zone de calme
- Zone II : Il s'agit de la zone perturbée par l'onde de détente qui s'étend progressivement à la fois vers l'amont et vers l'aval. Les caractéristiques $ C^- $ sont représentées par un faisceau de droites dont chacune représente le déplacement d'un point initialement situé à t=0 le long de la verticale du barrage. Ces droites caractéristiques ont pour équation:
$ \qquad C_i^-: \quad \dfrac{ dx }{ dt }=u-c $ le long de laquelle $ u-2c =Cste $
Pour connaitre les coordonnées du point $ P(x,t) $ situé initialement à une profondeur $ h $ de la verticale du barrage à l'instant $ t=0 $, nous pouvons remarquer que ce point se situe à l'intersection de la caractéristique négative du faisceau d'onde de détente $ C_- $ avec une caractéristique positive en provenance de l'amont $ C_+ $.
Il nous faut donc "remonter" la caractéristique $ C_+ $ sur laquelle la quantité $ c+2u $ se conserve. A son intersection avec l'axe des $ x $ à $ t=0 $, les valeurs de la vitesse et de la célérité sont : $ u_0=0 $ et $ c_{1}=2\sqrt{gh_1} $.
Nous obtenons ainsi la valeur de la célérité de l'onde en ce point $ P $:
$ c_{t1}=\dfrac{ dx }{ dt }=u-c=-3c+2c_1=-3\sqrt{gh}+2\sqrt{gh_1} $
Ces 3 zones sont délimitées par des caractéristiques frontières:
- Zone I - Zone II: Cette caractéristique représente la propagation du point supérieur du barrage à la célérité $ c_{t1} $ :
$ \qquad C_1^-: \quad \dfrac{ dx }{ dt }=u_1-c_1 $. Or $ u_{1}=0 $, soit $ c_{t1}=-\sqrt{gh_1} $
- Zone II - Zone III: . Cette caractéristique frontière représente la propagation du front d'onde de détente sur le fond sec à l'aval. Dans l'expression générale valable dans la Zone II, nous obtenons:
De l'expression générale de la célérité valable en zone 2 nous en déduisons pour la point de hauteur $ h_1} $:
Le front d'onde sur font sec se déplace donc à une célérité double de celle de l'onde de régression amont.
Reprenons donc l'expression de la célérité de l'onde de détente:
$ \qquad C_t^-: \quad \dfrac{ dx }{ dt }=-3\sqrt{gh}+2\sqrt{gh_1} $
La courbe de la surface libre s'obtient en intégrant cette dernière relation, ce qui donné:
$ \qquad C_t^-: \quad \dfrac{ x }{ t }=-3\sqrt{gh}+2\sqrt{gh_1} $
Dans l'espace $ (h,x) $, nous obtenons l'équation suivante:
$ h=\dfrac{ 1 }{ 9g }(\dfrac{ x }{ t }-2\sqrt{gh_1}) $
qui correspond à un faisceau de paraboles qui passent toutes par le point fixe d'équation: $ h_f=\dfrac{ 4 }{ 9 } h_1 $
En ce point, la vitesse du courant est égale à :
$ u_f+2c_f=2\sqrt{gh_1} \qquad \Rightarrow\qquad u_f=2\sqrt{gh}+2\sqrt{gh_1} $
$ u_f=-2\sqrt{g \dfrac{ 4 }{ 9} h_1}+2\sqrt{gh_1}=\dfrac{ 2 }{ 3}\sqrt{gh_1} $
et le débit transitant dans la section de la vanne:
$ u_fh_f=\dfrac{ 2 }{ 3} \sqrt{gh_1}\dfrac{ 4}{ 9}h_1=\dfrac{ 8 }{ 27} h_1\sqrt{gh_1} $
Les courbes suivantes représentent les évolutions normalisées des grandeurs: $ \dfrac{ c_t }{ c_1} ; \dfrac{ c}{ c_1} ;\dfrac{ u }{ c_1} $
avec : $ c_1=\sqrt{gh_1}; c=\sqrt{gh}, h_*=h/h_1 $
$ \dfrac{ c_t }{ c_1}=-3\sqrt{h_*}+2; \dfrac{ c_ }{ c_1}=\sqrt{h_*}; \dfrac{ u }{ c_1}=-2\sqrt{h_*}+2 $
Essais CNR Les essais CNR n'ont pas été réalisés strictement dans les conditions idéales de la théorie de Ritter : la canal a été utilisé avec une pente du fond et une ligne d'eau se rapprochant du régime normal d'écoulement. Les vitesses de propagation du front sec mesurées dans les différents essais sont répertoriées dans le tableau ci-dessous.
Théorie de Stoker
Stoker (1957) compléta la théorie de Ritter en traitant des configurations plus complètes, toujours par la théorie des caractéristiques. Nous nous intéresserons ici à la prise en compte d'une lame d'eau à l'aval du barrage.
Le problème à résoudre est très semblable au précédent, si ce n'est la présence de la lame d'eau d'épaisseur $ h_a $ à l'aval de la zone de rupture du barrage.
Nous sommes donc toujours dans la situation du développement d'un faisceau d'ondes de détente dans la Zone II. Les zones I et III sont des zones de calme, mais dans laquelle apparait une onde de compression.
.
Comme l'indique Graf [4], la seule possibilité pour relier le profil de l'onde négative avec la surface libre est de créer une discontinuité sous la forme d'une onde positive d'amont, d'une profondeur $ h_2 $.
Nous identifions 2 points particuliers:
- le point $ C $, qui délimite la zoned e transition caractérisée par l'onde où la profondeur d'eau est $ h_2 $. et la vitesse $ U_2 $. A l'aval de $ C $, la profondeur d'eau est $ h_0 $ et la vitesse $ U_0=0 $
- le point B qui délimite l'onde négative d'aval caractérisée par la vitesse $ U(h)=U_1-2\sqrt{gh}+2\sqrt{gh_1} $ et la zone de transition $ h_2,U_2 $
Par ailleurs, nous avons vu que l'équation de continuité pour l'onde positive est donnée par:
$ (U_0-C_{tc})h_0=(U_2-C_{tc})h_2 $
Soit : $ C_{tc})(h_2-h_0)=U_2h_2 $
L'introduction de la valeur de la vitesse de l'onde négative d'aval : $ U(h)=-2\sqrt{gh_2}+2\sqrt{gh_1} $ , nous donne:
$ C_{tc}=\dfrac{ (-2\sqrt{gh_2}+2\sqrt{gh_1})h_2 }{ h_2-h_0 } $
Par ailleurs, nous avions vu que la relation de continuité nous a permis d'obtenir:
$ C_{tc}=\sqrt{gh_0}\sqrt{\dfrac{h_2}{ 2h_0} (1+\dfrac{h_2}{ h_0})}} $
La comparaison de ces 2 relations nous permet de calculer les valeurs de $ C_{tc} $ et de $ h_2 $ par itérations.
Nous poserons: $ H_2=\dfrac{h_2}{ h_0}) $ et $ H_1=\dfrac{h_1}{ h_0}) $
Il vient pour calculer $ H_2 $:
$ 2(1-\sqrt{H_2} )\dfrac{H_2}{ H_2-H_1} =\sqrt{\dfrac{H_2}{ 2} (1+\dfrac{H_2}{ H_1} ) } $
D'où les expressions de la vitesse de l'eau:
$ \dfrac{U_2}{ C_1}= 2(1-\sqrt{H_2} ) $
et la célérité du front d'onde:
$ \dfrac{C_{tc}}{ C_1}= \dfrac{2H_2}{ H_2-H_1} (1-\sqrt{H_2} ) $
Ces 3 courbes correspondent à ces relations sont fournies ci-après:
Essais CNR
réalisation d'essais physiques à la CNR
Plusieurs essais physiques ont été réalisés à la CNR sur le canal de laboratoire dont les dimensions sont les suivantes:
à rédiger
Les résultats mettent
Bibliographie
- Stoker A., 1975, "Water waves", Intersciences Pub. Inc. New York, USA
- Hydraulique fluviale - vol. 16 - Ecoulement et phénomènes de transport dans les canaux à géométrie simple, 628 p., Presses Polytechniques et Universitaires Romandes, 2000
Remerciements
Les auteurs expriment leurs remerciements à :
- CNR
- Laurence Duchenne, Pierre Roumieu et Pierre Balayn ainsi qu'à tous les personnels de la CNR qui ont aidé à la réalisation de ces essais
- ENTPE
- Bernard Clément responsable du projet FORM@HYDRO
Les auteurs
Jean-Michel Tanguy William Chloé Angeline Emmanuelle
 S'abonner à un flux RSS
S'abonner à un flux RSS