S'abonner à un flux RSS
Bernoulli (théorème de) (HU) : Différence entre versions
De Wikhydro
| Ligne 3 : | Ligne 3 : | ||
Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et permanent. | Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et permanent. | ||
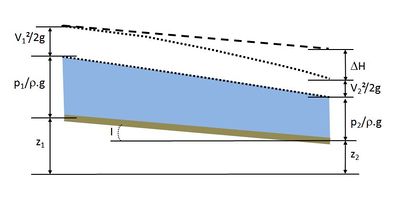
| − | Il s'écrit en particulier, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2), sous la forme suivante : | + | Il s'écrit en particulier, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2 - voir ''figure'' 1), sous la forme suivante : |
| − | <center><math>\frac{V_1^2}{2.g}+\frac{p_1}{ρ.g}+z_1=\frac{ | + | <center><math>\frac{V_1^2}{2.g}+\frac{p_1}{ρ.g}+z_1=\frac{V_21^2}{2.g}+\frac{p_2}{ρ.g}+z_2+Δh</math></center> |
| Ligne 21 : | Ligne 21 : | ||
| − | + | [[File:bernoulli.JPG|400px|center|thumb|<center>''Représentation des différentes grandeurs dans l'équation de Bernoulli.''</center>]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Représentation des différentes grandeurs dans l'équation de Bernoulli. | + | |
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
Version du 23 janvier 2020 à 11:30
Traduction anglaise : Bernoulli's equation
Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et permanent.
Il s'écrit en particulier, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2 - voir figure 1), sous la forme suivante :
Avec :
- $ V $ : vitesse ($ m/s $) ;
- $ p $ : pression (pression atmosphérique si écoulement à surface libre) ($ P $a) ;
- $ h $ : hauteur d'eau ($ m $) ;
- $ ρ $ : masse volumique ($ kg/m^3 $) ;
- $ g $ : accélération de la pesanteur ($ m/s^2 $) ;
- $ Δh $ : pertes de charge dues aux frottements sur les parois et à la viscosité entre les sections 1 et 2 ($ m $).
Dans cette expression, l'énergie est exprimée en hauteur de fluide. Voir Charge hydraulique.
