Courant-Friedrich-Levy / CFL (condition de) (HU) : Différence entre versions
m (Bernard Chocat a déplacé la page Courant-Friedrich-Levy (condition de) (HU) vers Courant-Friedrich-Levy / CFL (condition de) (HU) : titre complété par son acronyme) |
|||
| Ligne 2 : | Ligne 2 : | ||
<u>Dernière mise à jour</u> : 21/4/2020 | <u>Dernière mise à jour</u> : 21/4/2020 | ||
| + | |||
| + | Condition nécessaire pour qu'un schéma numérique produise une solution cohérente lors de la résolution d'une équation aux dérivées partielles hyperboliques (ou pour un système d'équations aux dérivées partielles). | ||
| + | |||
| + | ==Éléments d'historique== | ||
| + | |||
| + | La condition CFL porte le nom de trois mathématiciens allemands (Richard Courant, Kurt Friedrichs et Hans Lewy) qui ont publié en 1928 un article concernant l’analyse d’équations aux dérivées partielles et leur approximation numérique. Cet article mettait en évidence une condition nécessaire pour qu’un algorithme de calcul produise une solution cohérente. Cet article très en avance sur son temps a trouvé un intérêt majeur avec le développement des ordinateurs permettant la mise en œuvre de différentes méthodes numériques de résolution consistant à discrétiser le domaine de travail en pas de temps <math>Δt</math> et en pas d'espace <math>Δx</math>. | ||
| + | |||
| + | Cette condition se met sous la forme : | ||
| + | |||
| + | <center><math>\frac{Δx}{Δt}\ ≥\ c</math></center> | ||
| + | |||
| + | <u>Nota</u> : la quantité <math>C_0 = c\frac{Δt}{Δx}</math> est appelé Nombre de Courant. | ||
| + | |||
| + | ==Cas des équations d'onde== | ||
| + | |||
| + | === Interprétation intuitive de la condition CSL=== | ||
| + | |||
| + | Considérons un plan d'eau parfaitement tranquille. A l'instant <math>t = 0</math>, on jette un caillou en un point particulier de ce plan d'eau. Ce caillou provoque l'apparition d'ondes qui se déplacent à partir du point d'impact. Si l'on trace une droite passant par le point d'impact et que l'on représente par la variable <math>x</math> la position d'un point sur cet axe, il est possible de représenter le déplacement de la première onde dans un repère <math>x, t</math> (<math>t</math> représentant le temps). | ||
| + | |||
| + | |||
| + | [[File:caractéristiques1.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Représentation schématique de la propagation d'une perturbation dans l'espace abscisse-temps.''</center>]] | ||
| + | |||
| + | Les deux courbes obtenues sont les courbes caractéristiques de l'équation régissant le phénomène. Elles séparent le domaine en deux sous-domaines aux propriétés très différentes : | ||
| + | * la partie non hachurée n'est pas encore perturbée par le fait que l'on a jeté un caillou. En fait, l'information « on a jeté un caillou » n'est pas encore arrivé jusqu'en ces points ; | ||
| + | * la partie hachurée, pour sa part a reçu l'information et son état dépend du fait que l'on a jeté un caillou. | ||
| + | |||
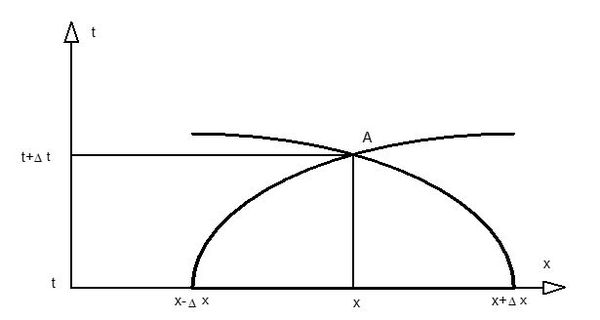
| + | Considérons par exemple un point quelconque <math>A</math>, situé à l'abscisse <math>x</math> et au temps <math>t</math>. Ce point est situé à l'intersection de deux courbes caractéristiques, l'une provenant de la droite et l'autre de la gauche (des <math>x</math> négatifs et des <math>x</math> positifs). Au temps <math>t - Δt</math>, ces deux courbes passaient respectivement par les positions <math>x - Δx</math> et <math>x + Δx</math>. Ceci signifie que l'état du milieu au point <math>x</math> dépend de l'état du milieu au temps <math>t - Δt</math> entre les points <math>x - Δx</math> et <math>x + Δx</math>, mais qu'il est indépendant de l'état du milieu au même instant et à l'extérieur de ce domaine, l'information n'ayant pas eu le temps d'arriver jusqu'à l'abscisse <math>x</math>. | ||
| + | |||
| + | |||
| + | [[File:caractéristique2.JPG|600px|center|thumb|<center>''<u>Figure 2</u> : Domaine d'influence du point <math>A</math>.''</center>]] | ||
| + | |||
| + | Ceci montre qu’il existe une relation entre la [[Célérité (HU)|célérité]] de l’onde, <math>c</math> et les pas de temps, <math>Δt</math> et d’espace, <math>Δx</math>, qui doit être vérifiée pour assurer la [[Stabilité (HU)|stabilité]] du schéma de résolution. On retrouve ainsi facilement la condition CSL entre les pas de temps et d'espace : | ||
| + | |||
| + | |||
| + | <center><math>\frac{Δx}{Δt}\ ≥\ c</math></center> | ||
| + | |||
| + | ===Cas des ondes se propageant dans un fluide en mouvement=== | ||
| + | |||
| + | Si les ondes se propagent dans un milieu qui est lui-même en mouvement, l'eau s'écoulant de l'amont vers l'aval à la vitesse <math>V</math>, la vitesse des ondes para rapport à un repère fixe va être différente selon que l'onde va vers l'amont ou vers l'aval. Le déplacement des ondes dans un repère fixe <math>x, t</math> s'effectuera à la vitesse <math>V + c</math> pour l'onde « descendante » (allant de l'amont vers l'aval) et à la vitesse <math>V - c</math> pour l'onde « montante ». | ||
| + | |||
| + | La condition de Courant-Friedrisch-Levy s'écrit alors : | ||
| + | |||
| + | |||
| + | <center><math>\frac{Δx}{Δt}\ ≥\ |V\ ±\ c|</math></center> | ||
| + | |||
| + | Il est important de préciser que l'établissement de cette condition nécessite que la dérivée seconde de la relation entre la section mouillée et la hauteur soit nulle, c'est-à-dire pratiquement, que la section soit rectangulaire. On peut également noter que si l'onde se déplace moins vite que l'eau (<math>c < V</math>), les deux ondes vont de l'amont vers l'aval. Il s'agit alors d'un régime hypercritique ([[Ecoulement torrentiel (HU)|torrentiel]]) dont la résolution nécessite deux conditions aux limites à l'amont, alors que dans le cas d'un régime [[Ecoulement fluvial (HU)|fluvial]], la résolution se fait à partir d'une condition amont et d'une condition aval. | ||
| + | |||
| + | ===Évaluation de la vitesse de l'onde=== | ||
| + | |||
| + | |||
| + | |||
| + | == Utilisation de la méthode des caractéristiques pour résoudre les équations de Barré de Saint Venant== | ||
| + | |||
| + | En hydraulique, cette méthode a parfois été utilisée pour résoudre le système d'équations de [[Barré de Saint Venant (équations de) (HU)|Barré de Saint Venant]]. Elle est maintenant tombée en désuétude. | ||
| + | |||
| + | |||
| + | |||
Condition permettant de vérifier la [[Stabilité (HU)|stabilité]] des schémas de [[Différences finies (méthode des) (HU)|différences finies]] | Condition permettant de vérifier la [[Stabilité (HU)|stabilité]] des schémas de [[Différences finies (méthode des) (HU)|différences finies]] | ||
| Ligne 19 : | Ligne 76 : | ||
La condition de Courant-Friedrisch-Lewy est souvent utilisée pour d'autres schémas que celui pour lequel elle a été établie. Dans de nombreux cas, il est possible de choisir une valeur de pas de temps supérieure à celle donnée par cette relation. | La condition de Courant-Friedrisch-Lewy est souvent utilisée pour d'autres schémas que celui pour lequel elle a été établie. Dans de nombreux cas, il est possible de choisir une valeur de pas de temps supérieure à celle donnée par cette relation. | ||
| + | |||
| + | <u>Bibliographie</u> : | ||
| + | * Courant, R., Friedrichs, K. et Lewy,H. : On the Partial Difference Equations of Mathematical Physics ; Mathematische Annalen 100 ; 32-74 (téléchargeable sur http://www.stat.uchicago.edu/~lekheng/courses/302/classics/courant-friedrichs-lewy.pdf. | ||
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
Version du 21 avril 2020 à 13:41
Traduction anglaise : Courant-Friedrich-Levy's condition
Dernière mise à jour : 21/4/2020
Condition nécessaire pour qu'un schéma numérique produise une solution cohérente lors de la résolution d'une équation aux dérivées partielles hyperboliques (ou pour un système d'équations aux dérivées partielles).
Sommaire |
Éléments d'historique
La condition CFL porte le nom de trois mathématiciens allemands (Richard Courant, Kurt Friedrichs et Hans Lewy) qui ont publié en 1928 un article concernant l’analyse d’équations aux dérivées partielles et leur approximation numérique. Cet article mettait en évidence une condition nécessaire pour qu’un algorithme de calcul produise une solution cohérente. Cet article très en avance sur son temps a trouvé un intérêt majeur avec le développement des ordinateurs permettant la mise en œuvre de différentes méthodes numériques de résolution consistant à discrétiser le domaine de travail en pas de temps $ Δt $ et en pas d'espace $ Δx $.
Cette condition se met sous la forme :
Nota : la quantité $ C_0 = c\frac{Δt}{Δx} $ est appelé Nombre de Courant.
Cas des équations d'onde
Interprétation intuitive de la condition CSL
Considérons un plan d'eau parfaitement tranquille. A l'instant $ t = 0 $, on jette un caillou en un point particulier de ce plan d'eau. Ce caillou provoque l'apparition d'ondes qui se déplacent à partir du point d'impact. Si l'on trace une droite passant par le point d'impact et que l'on représente par la variable $ x $ la position d'un point sur cet axe, il est possible de représenter le déplacement de la première onde dans un repère $ x, t $ ($ t $ représentant le temps).
Les deux courbes obtenues sont les courbes caractéristiques de l'équation régissant le phénomène. Elles séparent le domaine en deux sous-domaines aux propriétés très différentes :
- la partie non hachurée n'est pas encore perturbée par le fait que l'on a jeté un caillou. En fait, l'information « on a jeté un caillou » n'est pas encore arrivé jusqu'en ces points ;
- la partie hachurée, pour sa part a reçu l'information et son état dépend du fait que l'on a jeté un caillou.
Considérons par exemple un point quelconque $ A $, situé à l'abscisse $ x $ et au temps $ t $. Ce point est situé à l'intersection de deux courbes caractéristiques, l'une provenant de la droite et l'autre de la gauche (des $ x $ négatifs et des $ x $ positifs). Au temps $ t - Δt $, ces deux courbes passaient respectivement par les positions $ x - Δx $ et $ x + Δx $. Ceci signifie que l'état du milieu au point $ x $ dépend de l'état du milieu au temps $ t - Δt $ entre les points $ x - Δx $ et $ x + Δx $, mais qu'il est indépendant de l'état du milieu au même instant et à l'extérieur de ce domaine, l'information n'ayant pas eu le temps d'arriver jusqu'à l'abscisse $ x $.
Ceci montre qu’il existe une relation entre la célérité de l’onde, $ c $ et les pas de temps, $ Δt $ et d’espace, $ Δx $, qui doit être vérifiée pour assurer la stabilité du schéma de résolution. On retrouve ainsi facilement la condition CSL entre les pas de temps et d'espace :
Cas des ondes se propageant dans un fluide en mouvement
Si les ondes se propagent dans un milieu qui est lui-même en mouvement, l'eau s'écoulant de l'amont vers l'aval à la vitesse $ V $, la vitesse des ondes para rapport à un repère fixe va être différente selon que l'onde va vers l'amont ou vers l'aval. Le déplacement des ondes dans un repère fixe $ x, t $ s'effectuera à la vitesse $ V + c $ pour l'onde « descendante » (allant de l'amont vers l'aval) et à la vitesse $ V - c $ pour l'onde « montante ».
La condition de Courant-Friedrisch-Levy s'écrit alors :
Il est important de préciser que l'établissement de cette condition nécessite que la dérivée seconde de la relation entre la section mouillée et la hauteur soit nulle, c'est-à-dire pratiquement, que la section soit rectangulaire. On peut également noter que si l'onde se déplace moins vite que l'eau ($ c < V $), les deux ondes vont de l'amont vers l'aval. Il s'agit alors d'un régime hypercritique (torrentiel) dont la résolution nécessite deux conditions aux limites à l'amont, alors que dans le cas d'un régime fluvial, la résolution se fait à partir d'une condition amont et d'une condition aval.
Évaluation de la vitesse de l'onde
Utilisation de la méthode des caractéristiques pour résoudre les équations de Barré de Saint Venant
En hydraulique, cette méthode a parfois été utilisée pour résoudre le système d'équations de Barré de Saint Venant. Elle est maintenant tombée en désuétude.
Condition permettant de vérifier la stabilité des schémas de différences finies
explicites parfois utilisés pour résoudre numériquement les équations de Barré de Saint Venant.
Cette condition s'exprime sous la forme :
Avec :
- $ Δx $ : pas d'espace ($ m $) ;
- $ Δt $ : pas de temps ($ s $) ;
- $ V $ : vitesse ($ m/s $) ;
- $ g $ : accélération de la pesanteur ($ m/s^2 $) ;
- $ h $ : hauteur de l'eau ($ m $).
La condition de Courant-Friedrisch-Lewy est souvent utilisée pour d'autres schémas que celui pour lequel elle a été établie. Dans de nombreux cas, il est possible de choisir une valeur de pas de temps supérieure à celle donnée par cette relation.
Bibliographie :
- Courant, R., Friedrichs, K. et Lewy,H. : On the Partial Difference Equations of Mathematical Physics ; Mathematische Annalen 100 ; 32-74 (téléchargeable sur http://www.stat.uchicago.edu/~lekheng/courses/302/classics/courant-friedrichs-lewy.pdf.
 S'abonner à un flux RSS
S'abonner à un flux RSS