Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/DAVID-POULTIER-TORNES : Différence entre versions
(→Solution analytique) |
(→Discriminant nul : \alpha=2k) |
||
| Ligne 145 : | Ligne 145 : | ||
En prenant, k=1, L=1 et <math>\alpha=3</math>, on obtient cette allure : | En prenant, k=1, L=1 et <math>\alpha=3</math>, on obtient cette allure : | ||
| − | <center>[[File:Pente du fond exponentielle sortie libre discriminant nul.gif| | + | <center>[[File:Pente du fond exponentielle sortie libre discriminant nul.gif|600px]]</center> |
==== Discriminant négatif : <math> \alpha^2 < 4k^2 </math> ==== | ==== Discriminant négatif : <math> \alpha^2 < 4k^2 </math> ==== | ||
Version du 11 juin 2020 à 15:33
Le thème de l'étude a pour but de modéliser l'impact du changement climatique sur les côtes en quantifiant l'impact des houles sur le littoral.
Afin de modéliser les houles, l'étude utilise le modèle de Berkhoff (ou équation de pente douce) qui intègre la repésentation des phénomènes de réfraction des fonds, le shoaling, la diffraction et la réflexion des structures côtières comme les digues ou les jétées.
Les équations obtenues seront résolues par uné méthode analytique ainsi qu'une méthode semi analytique : l'homotopie.
Sommaire |
Equation de Berkhoff
Ce modèle a pour expression : $ \boxed{ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 } $
où $ \phi $ est le potentiel, k est le nombre d’onde fonction de la profondeur H et de la fréquence $ \omega $ (T est la période), par la relation implicite $ \omega^2=gk \tanh(kH) $ , C est la célérité de l’onde, Cg est la célérité de groupe des vagues.
Pour simplifier le problème, nous nous placerons dans le domaine des ondes longues, ce qui signifie que $ C=C_g=\sqrt{gH} $.
On peut alors déduire la hauteur de la houle : $ H_l(x)=\Re{(\phi)}/\left| \phi \right| $ et son évolution dans le temps: $ h(x,t)=\Re \left (H_l(x)e^{-i\omega t} \right ) $.
Canal uniforme plat avec sortie libre en amont
On s'intéresse à une onde se propageant dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une sortie libre en amont.
On se place dans un domaine monodimensionnel de profondeur constante. L'équation se simplifie alors en $ \frac{\partial^2 \phi}{\partial x^2}+k^2\phi=0 $
Cette équation correspond à l'équation de Helmholtz.
Solution analytique
La forme des solutions est donc de la forme $ \phi(x)=A\mathrm{e}^{-\mathrm{i}kx}+B\mathrm{e}^{\mathrm{i}kx} $ où A et B sont deux constantes à déterminer grâce aux conditions aux limites $ \phi=1 $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=\mathrm{i}k\phi $ en $ x=L $.
On trouve alors $ A=0 $ et $ B=1 $ d'où $ \phi(x)=\mathrm{e}^{\mathrm{i}kx} $.
On peut alors déduire la hauteur de houle car $ \phi(x,t)=\mathrm{e}^{\mathrm{i}(kx-\omega t)} $ d'où $ \boxed{h(x,t)=\cos (kx-\omega t)} $.
Résolution par homotopie
La relation d'homotopie s'écrit $ (1-p)\Phi_{xx} +p(\Phi_{xx}+k^{2}\Phi)=0 $ qui se simplifie en $ \Phi_{xx} +pk^{2}\Phi=0 $. On prend $ u_{0}=0 $.
Ordre 0: L'équation s'écrit $ \Phi_{0,xx}=0 $.
Ainsi, on a $ \Phi_0=Ax+B $ où $ A $ et $ B $ sont deux constantes à déterminer avec les conditions aux limites énoncées précedemment.
On en déduit alors $ A=\frac{ik}{1-ikL} $ et $ B=1 $.
Finalement, on a $ \boxed{\Phi_0(x)=1+\dfrac{ik}{1-ikL}x} $.
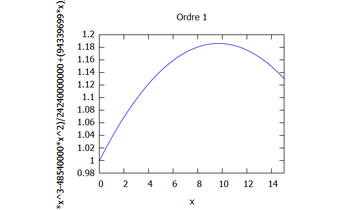
Ordre 1: L'équation s'écrit $ \Phi_{1,xx}+k^2\Phi_0=0 $.
Ainsi, on a $ \displaystyle\Phi_1+\iint\Phi_0+Ax+B=0 $. Pour déterminer les deux constantes, il faut choisir comme condition en amont $ \Phi_1(0)=0 $ puisque la condition $ \Phi_1(0)=1 $ a déjà été utilisé.
On en déduit alors $ A=\frac{3k^{2}L-2k^{4}L^{3}-3\mathrm{i}k^{3}L^{2}}{3(1-ikL)^{2}} $ et $ B=0 $.
Finalement, on a $ \boxed{\Phi_1(x)=-k^{2}\dfrac{ik}{1-ikL}\dfrac{x^{3}}{6}-k^{2}\dfrac{x^{2}}{2}+\frac{3k^{2}L-2k^{4}L^{3}-3\mathrm{i}k^{3}L^{2}}{3(1-ikL)^{2}}x} $.
Ainsi, en déterminant tout les ordres jusqu'à un certain ordre $ n $ on obtient la solution $ \Phi(x)=\sum_{i=0}^{n}p^{i}\Phi_{i}(x) $. On peut alors évaluer ce polynôme en 1 et déterminer la hauteur de la houle en prenant les mêmes valeurs de constante que dans la simulation analytique.
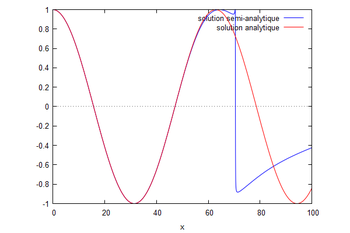
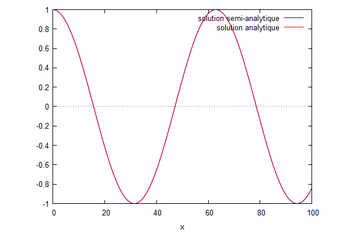
Canal uniforme unidimensionnel plat avec réflexion totale en amont
On s'intéresse à une onde se propageant dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire ainsi qu'une condition de flux aval précisée plus loin et une réflexion totale en amont.
L'équation reste la même que dans le cas n°1 : $ \frac{\partial^2 \phi}{\partial x^2}+k^2\phi=0 $.
Solution analytique
La forme des solutions est donc toujours de la forme $ \phi(x)=A\mathrm{e}^{-\mathrm{i}kx}+B\mathrm{e}^{\mathrm{i}kx} $ où A et B sont deux constantes à déterminer grâce aux conditions aux limites $ \frac{\partial \phi}{\partial x}=\mathrm{i}k(2-\phi) $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=0 $ en $ x=L $.
On trouve alors $ A=\mathrm{e}^{2\mathrm{i}kL} $ et $ B=1 $.
On en déduit alors $ \phi(x,t)=\mathrm{e}^{-\mathrm{i}(k(x-2L)+\omega t)}+\mathrm{e}^{\mathrm{i}(kx-\omega t)} $ et donc $ h(x,t)=\frac{\cos (kx-\omega t)+\cos(k(x-2L)+\omega t)}{\sqrt{2(1+\cos(2k(x-L))}} $ qui se simplifie en $ \boxed{h(x,t)=cos(kL-\omega t)} $.
Résolution par homotopie
La relation d'homotopie s'écrit toujours $ (1-p)\Phi_{xx} +p(\Phi_{xx}+k^{2}\Phi)=0 $ qui se simplifie en $ \Phi_{xx} +pk^{2}\Phi=0 $. On prend $ u_{0}=0 $.
Ordre 0: L'équation s'écrit $ \Phi_{0,xx}=0 $.
Ainsi, on a $ \Phi_0=Ax+B $ où $ A $ et $ B $ sont deux constantes à déterminer avec les conditions aux limites énoncées précedemment.
On en déduit alors $ A=0 $ et $ B=1 $.
Finalement, on a $ \boxed{\Phi_0(x)=2} $.
Ordre 1: L'équation s'écrit $ \Phi_{1,xx}+k^2\Phi_0=0 $.
Ainsi, on a $ \displaystyle\Phi_1+\iint\Phi_0+Ax+B=0 $.
On en déduit alors $ A=2k^{2}L $ et $ B=2+2\mathrm{i}kL $.
Finalement, on a $ \boxed{\Phi_1(x)=-k^{2}x^{2}+2k^{2}Lx+2+2\mathrm{i}kL} $.
Canal uniforme unidimensionnel avec pente du fond constante
On s'intéresse à une onde se propageant dans un domaine monodimensionnel de longueur L avec pente du fond constante avec entrée par l'aval d'une onde fréquence unitaire et une sortie libre en amont. On supposera que le nombre d'onde $ k $ est constant.
On se place dans un domaine monodimensionnel avec pente du fond constante. On va noter la pente $ H(x)=H_0-\alpha x $ où $ H_0 $ correspond à la hauteur initiale du fond et $ \alpha $ correspond à la pente du fond.
L'équation s'écrit donc :
$ (H_0-\alpha x)\frac{\partial^2 \phi}{\partial x^2}-\alpha \frac{\partial \phi}{\partial x}+k^2(H_0-\alpha x)\phi=0 $
On effectue alors le changement de variable $ X=\frac{k}{\alpha}(H_0-\alpha x) $. L'équation devient alors :
$ \alpha kX\frac{\partial^2 \phi}{\partial X^2}+\alpha k\frac{\partial \phi}{\partial X}+\alpha kX\phi=0 $
En divisant alors par $ \alpha k $ et en multipliant par $ X $, on obtient alors l'équation de Bessel suivante :
$ X^2\frac{\partial^2 \phi}{\partial X^2}+X\frac{\partial \phi}{\partial X}+X^2\phi=0 $
Solution analytique
La forme des solutions est donc de la forme $ \phi(X)=AJ_0(X)+BY_0(X) $ où $ J_0 $ et $ Y_0 $ correspondent aux fonctions de Bessel respectivement de première et de deuxième espèce.
On effectue alors le changement de variable inverse :
$ \phi(x)=AJ_0(\frac{k}{\alpha}(\alpha x-H_0))+BY_0(\frac{k}{\alpha}(px-H_0)) $.
On pose $ x_L=\frac{k}{\alpha}(\alpha L-H_0) $ et $ x_0=-\frac{k}{\alpha}H_0 $.
On trouve alors $ A=\frac{Y_1(x_L)-\mathrm{i}Y_0(x_L)}{\epsilon} $ et $ B=\frac{J_1(x_L)+\mathrm{i}J_0(x_L)}{\epsilon} $ en posant $ \epsilon=(Y_1(x_L)-\mathrm{i}Y_0(x_L))J_0(x_0)+(J_1(x_L)+\mathrm{i}J_0(x_L))Y_0(x_0) $.
Résolution par homotopie
Equation différentielle: $ \frac{\partial ^{2}\Phi }{\partial x^{2}}-\frac{c}{H_{0}-cx}\frac{\partial \Phi }{\partial x}+k^{2}\Phi =0 \\ $
L'homotopie donne : $ (1-p)\lbrack \Phi _{xx}-u_{0,xx}\rbrack +p\lbrack \Phi _{xx}+\frac{c}{H_{0}-cx}\Phi _{x}-k^{2}\Phi \rbrack =0\\ $
Ordre 0 :$ \Phi _{0,xx}-u_{0,xx}=0\\ $
Ordre 1 :$ \Phi _{1,xx}-k^{2}\Phi _{0}+\frac{c}{H_{0}-cx}\Phi _{0,x}=0 \\ $
Ordre 2 : $ \Phi _{2,xx}-k^{2}\Phi _{1}+\frac{c}{H_{0}-cx}\Phi _{1,x}=0 \\ $
Canal uniforme unidimensionnel avec pente du fond exponentielle
On s'intéresse à une onde se propageant dans un domaine monodimensionnel de longueur L avec pente du fond exponentiel avec entrée par l'aval d'une onde fréquence unitaire et une sortie libre en amont.
On se place dans un domaine monodimensionnel avec pente du fond exponentielle. On va noter la pente $ H(x)=H_0\mathrm{e}^{-\alpha x} $ où $ H_0 $ correspond à la hauteur initiale du fond et $ \alpha $ correspond à la pente du fond.
L'équation s'écrit donc :
$ \frac{\partial^2 \phi}{\partial x^2}-\alpha\frac{\partial \phi}{\partial x}+k^2\phi=0 $
On en déduit alors l'équation caractéristque : $ r^2-\alpha r+k^2 $ et ainsi le discrimant associé $ \Delta = \alpha^2 -4k^2 $. Il faut donc résoudre suivant la valeur du discriminant.
Solution analytique
Discriminant positif : $ \alpha^2 > 4k^2 $
On a $ \Delta=\alpha^2-4k^2>0 $. Alors on dispose de deux solutions réelles à savoir $ r_1 $ et $ r_2 $ telles que :
Les solutions sont donc de la forme $ A\mathrm{e}^{r_1x}+B\mathrm{e}^{r_2x} $ avec $ A $ et $ B $ deux constantes à déterminer grâce aux conditions aux limites $ \phi=1 $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=\mathrm{i}k\phi $ en $ x=L $.
On trouve alors $ A=\dfrac{(r_2-\mathrm{i}k)\mathrm{e}^{r_2L}}{(-r_1+\mathrm{i}k)\mathrm{e}^{r_1L}+(r_2-\mathrm{i}k)\mathrm{e}^{r_2L}} $ et $ B=\dfrac{(-r_1+\mathrm{i}k)\mathrm{e}^{r_1L}}{(-r_1+\mathrm{i}k)\mathrm{e}^{r_1L}+(r_2-\mathrm{i}k)\mathrm{e}^{r_2L}} $.
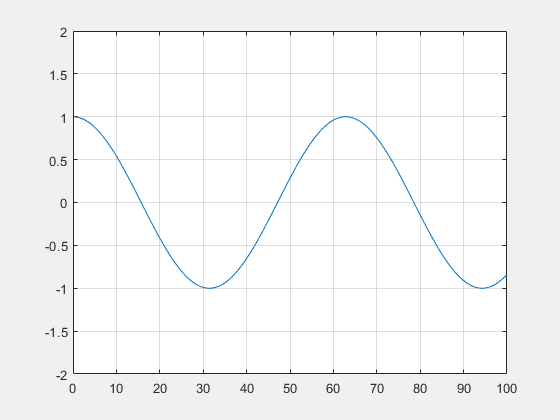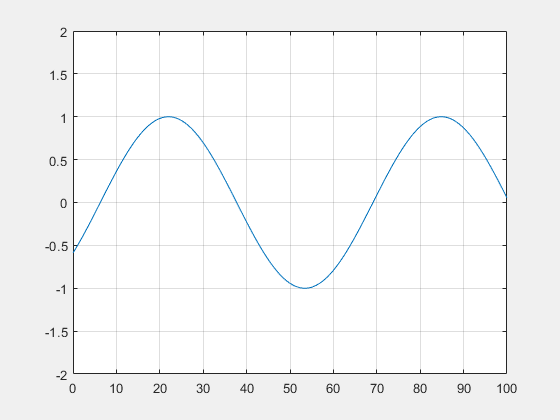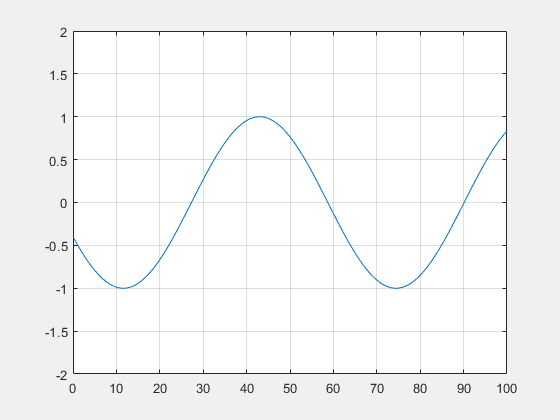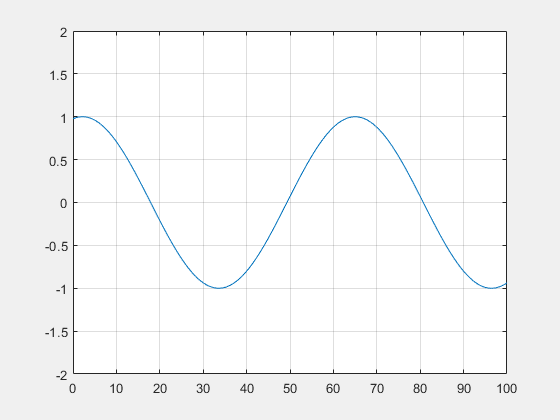
En prenant, k=1, L=1 et $ \alpha=3 $, on obtient cette allure :
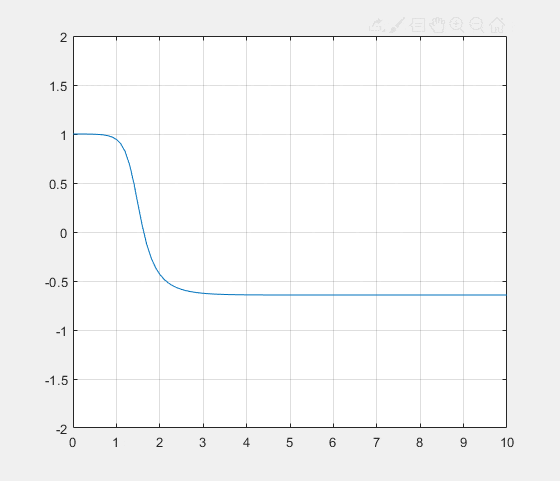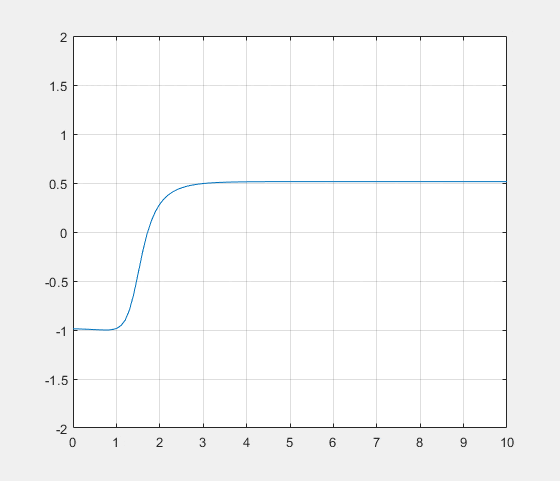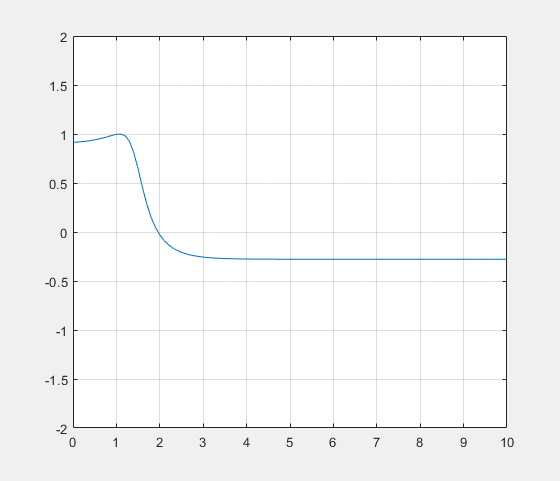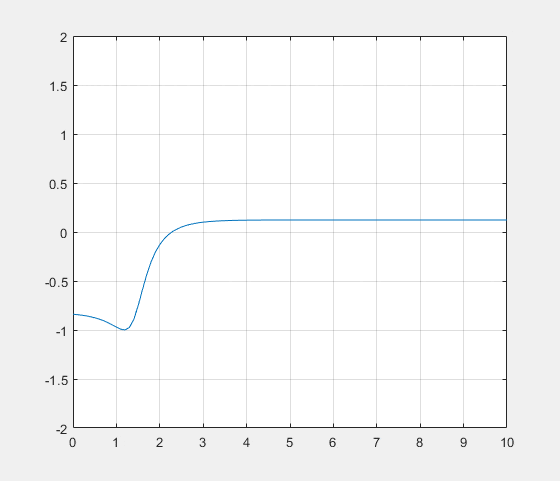
Discriminant nul : $ \alpha=2k $
On a $ \Delta=\alpha^2-4k^2=00 $. Alors on dispose d'une solution réelle telle que :
Les solutions sont donc de la forme $ (Ax+B)\mathrm{e}^{kx} $ avec $ A $ et $ B $ deux constantes à déterminer grâce aux conditions aux limites $ \phi=1 $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=\mathrm{i}k\phi $ en $ x=L $.
On trouve alors $ A=\dfrac{\mathrm{i}k-k}{1+kL-\mathrm{i}k} $ et $ B=1 $.
En prenant, k=1, L=1 et $ \alpha=3 $, on obtient cette allure :
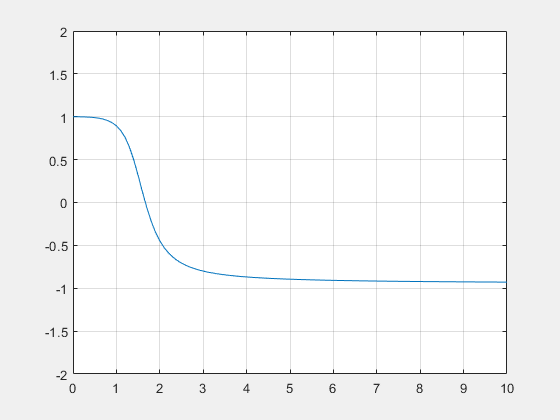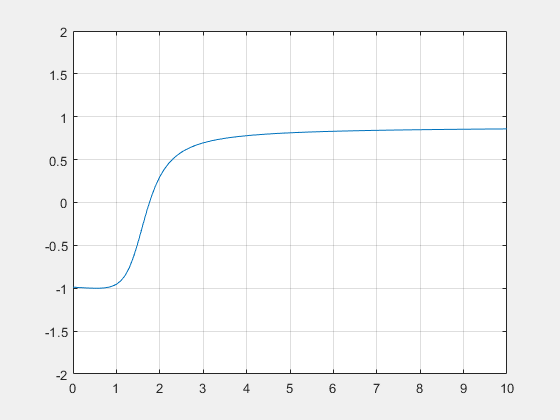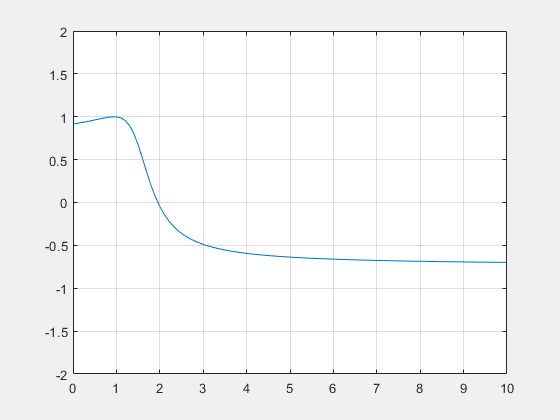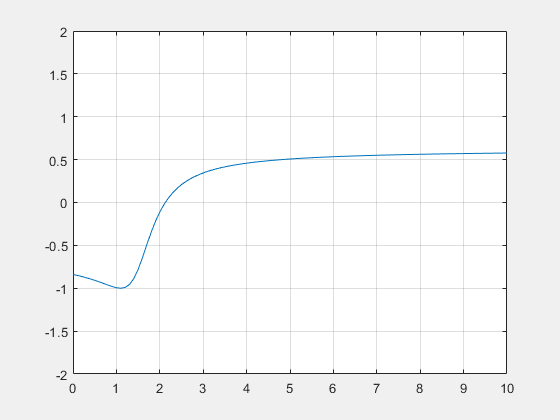
Discriminant négatif : $ \alpha^2 < 4k^2 $
On a $ \Delta=\alpha^2-4k^2<0 $. Alors on dispose de deux solutions complexes : $ x=\frac{\alpha}{2} \pm i\frac{\sqrt{\vert \alpha^{2}-4k^{2}\vert }}{2} \\ $
On pose :$ \gamma=\frac{\alpha}{2} $ et $ k' =\frac{\sqrt{\vert \alpha^{2}-4k^{2}\vert }}{2}\\ $.
Les solutions sont donc de la forme $ \phi (x)= \mathrm{e}^{\gamma x}(C_{1}\cos (k'x)+C_{2}\sin (k'x)) $ avec $ C_1 $ et $ C_2 $ deux constantes à déterminer grâce aux conditions aux limites énoncées précédemment.
On trouve alors $ C_1=1 $ et $ C_2=\dfrac{(\mathrm{i}k-\gamma)cos(k'L)+k'sin(k'L)}{(-\mathrm{i}k+\gamma)sin(k'L)+k'cos(k'L)} $.
Résolution par homotopie
Equation différentielle: $ \frac{\partial ^{2}\Phi }{\partial x^{2}}-c\frac{\partial \Phi }{\partial x}+k^{2}\Phi =0\\ $
L'homotopie donne : $ (1-p)\lbrack \Phi _{xx}-u_{0,xx}\rbrack +p\lbrack \Phi _{xx}+\alpha\Phi _{x}-k^{2}\Phi \rbrack =0\\ $
$ Ordre 0 :\Phi _{0,xx}-u_{0,xx}=0\\ $
$ Ordre 1 : \Phi _{1,xx}-k^{2}\Phi _{0}+\alpha\Phi _{0,x}=0\\ $
$ Ordre 2 : \Phi _{2,xx}-k^{2}\Phi _{1}+\alpha\Phi _{1,x}=0\\ $
 S'abonner à un flux RSS
S'abonner à un flux RSS