Top Model (HU) : Différence entre versions
| (Une révision intermédiaire par un utilisateur est masquée) | |||
| Ligne 5 : | Ligne 5 : | ||
==Principes du modèle== | ==Principes du modèle== | ||
| − | Le principe de base du modèle consiste à supposer que lorsque le sol arrive à saturation, l'eau peut s'écouler dans le sol, parallèlement à la pente, sous la forme d'un écoulement de subsurface. L'écoulement est donc principalement commandé par la topographie (d'où le nom : TOPographie based MODEL). Ce modèle nécessite donc sur une connaissance fine de la topographie obtenue par l'utilisation d'un [[Modèle numérique de terrain / MNT (HU)|modèle numérique de terrain]] permettant de mailler finement le bassin versant. | + | Le principe de base du modèle consiste à supposer que lorsque le sol arrive à saturation, l'eau peut s'écouler dans le sol, parallèlement à la pente, sous la forme d'un [[Ecoulement hypodermique (HU)|écoulement de subsurface]]. L'écoulement est donc principalement commandé par la topographie (d'où le nom : TOPographie based MODEL). Ce modèle nécessite donc sur une connaissance fine de la topographie obtenue par l'utilisation d'un [[Modèle numérique de terrain / MNT (HU)|modèle numérique de terrain]] permettant de mailler finement le bassin versant (figure 1). |
L'écoulement lui-même est supposé s'effectuer dans les couches superficielles du sol et le modèle le représente en utilisant la [[Darcy (loi de) (HU)|loi de Darcy]] pour les milieux saturés. | L'écoulement lui-même est supposé s'effectuer dans les couches superficielles du sol et le modèle le représente en utilisant la [[Darcy (loi de) (HU)|loi de Darcy]] pour les milieux saturés. | ||
| + | |||
| + | |||
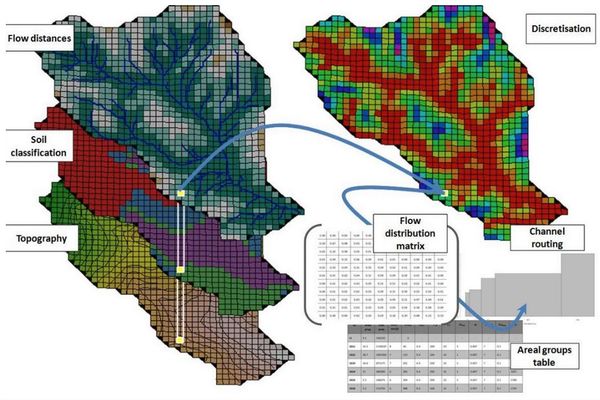
| + | [[File:top model.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Exemple de représentation d'un bassin versant pour utiliser top model ; <u>Source</u> : Metcalfe ''et al.''(2015)''</center>]] | ||
==Formulation mathématique== | ==Formulation mathématique== | ||
| Ligne 18 : | Ligne 21 : | ||
| − | *et une équation traduisant l'évolution de la transmissivité hydraulique : | + | * et une équation traduisant l'évolution de la transmissivité hydraulique en fonction de la saturation du sol : |
| Ligne 30 : | Ligne 33 : | ||
* <math>T(t)</math> : [[Transmissivité (HU)|transmissivité hydraulique]] à l'instant t (m<sup>2</sup>/s) ; | * <math>T(t)</math> : [[Transmissivité (HU)|transmissivité hydraulique]] à l'instant t (m<sup>2</sup>/s) ; | ||
* <math>T_0</math> : transmissivité hydraulique à saturation, égale au produit de la profondeur du sol par la [[Conductivité hydraulique (HU)|conductivité hydraulique]] à saturation (m<sup>2</sup>/s) ; | * <math>T_0</math> : transmissivité hydraulique à saturation, égale au produit de la profondeur du sol par la [[Conductivité hydraulique (HU)|conductivité hydraulique]] à saturation (m<sup>2</sup>/s) ; | ||
| − | * <math>grad(h)</math> : [[Gradient hydraulique (HU)|gradient hydraulique]], généralement assimilé à la pente perpendiculairement à la frontière <math>Δx</math> (m/m) ; | + | * <math>grad(h)</math> : [[Gradient hydraulique (HU)|gradient hydraulique]], généralement assimilé à la pente de la surface perpendiculairement à la frontière <math>Δx</math> (m/m) ; |
* <math>Δx</math> : largeur de la frontière entre les deux mailles (m) ; | * <math>Δx</math> : largeur de la frontière entre les deux mailles (m) ; | ||
* <math>d(t)</math> : déficit local égal à la quantité d'eau qu'il faudrait infiltrer pour faire affleurer la zone saturée (m) ; | * <math>d(t)</math> : déficit local égal à la quantité d'eau qu'il faudrait infiltrer pour faire affleurer la zone saturée (m) ; | ||
| − | * <math>m</math> : paramètre de [[Calage d'un modèle (HU)|calage]] traduisant la variation de la transmissivité en fonction de la saturation du sol. | + | * <math>m</math> : paramètre de [[Calage d'un modèle (HU)|calage]] traduisant la variation de la transmissivité en fonction de la saturation du sol (m). |
<u>Bibliographie</u> : | <u>Bibliographie</u> : | ||
* Beven, K.J., Kirby, M.J. (1979) : ''A physically based, variable contributing area model of basin hydrology'' ; Hydrological Sciences Bulletin ; Vol 24-1 ; pp 43-69. | * Beven, K.J., Kirby, M.J. (1979) : ''A physically based, variable contributing area model of basin hydrology'' ; Hydrological Sciences Bulletin ; Vol 24-1 ; pp 43-69. | ||
| + | * Metcalfe, P., Beven, K.J., Freer, J. (2015) : ''Dynamic TOPMODEL: A new implementation in R and its sensitivity to time and space steps'' ; 41p. ; disponible sur [https://www.semanticscholar.org/paper/Dynamic-TOPMODEL%3A-A-new-implementation-in-R-and-its-Metcalfe-Beven/6d52231d726241f46d5979aaf48cdc42330c1da6 semanticscholar.org] | ||
| + | |||
| + | <u>Pour en savoir plus</u> : | ||
| + | * Obled, C., Zin, I. (2004) : TOPMODEL : principes de fonctionnement et application ; La houille blanche ; N°1 ; pp 65-77. | ||
Version actuelle en date du 29 avril 2022 à 16:00
Dernière mise à jour : 29/04/2022
Modèle hydrologique fondé sur l'hypothèse d'une augmentation dans le temps de la surface contributive due à la saturation progressive des sols (Beven et Kirby, 1979).
[modifier] Principes du modèle
Le principe de base du modèle consiste à supposer que lorsque le sol arrive à saturation, l'eau peut s'écouler dans le sol, parallèlement à la pente, sous la forme d'un écoulement de subsurface. L'écoulement est donc principalement commandé par la topographie (d'où le nom : TOPographie based MODEL). Ce modèle nécessite donc sur une connaissance fine de la topographie obtenue par l'utilisation d'un modèle numérique de terrain permettant de mailler finement le bassin versant (figure 1).
L'écoulement lui-même est supposé s'effectuer dans les couches superficielles du sol et le modèle le représente en utilisant la loi de Darcy pour les milieux saturés.
[modifier] Formulation mathématique
Le Top model repose sur deux équations :
- l'équation de Darcy :
- et une équation traduisant l'évolution de la transmissivité hydraulique en fonction de la saturation du sol :
Ces deux équations sont associées à l'équation de conservation sur chacune des mailles.
avec :
- $ Qs(t) $ : débit sortant de la maille par la frontière de largeur $ Δx $ à l'instant t (m3/s) ;
- $ T(t) $ : transmissivité hydraulique à l'instant t (m2/s) ;
- $ T_0 $ : transmissivité hydraulique à saturation, égale au produit de la profondeur du sol par la conductivité hydraulique à saturation (m2/s) ;
- $ grad(h) $ : gradient hydraulique, généralement assimilé à la pente de la surface perpendiculairement à la frontière $ Δx $ (m/m) ;
- $ Δx $ : largeur de la frontière entre les deux mailles (m) ;
- $ d(t) $ : déficit local égal à la quantité d'eau qu'il faudrait infiltrer pour faire affleurer la zone saturée (m) ;
- $ m $ : paramètre de calage traduisant la variation de la transmissivité en fonction de la saturation du sol (m).
Bibliographie :
- Beven, K.J., Kirby, M.J. (1979) : A physically based, variable contributing area model of basin hydrology ; Hydrological Sciences Bulletin ; Vol 24-1 ; pp 43-69.
- Metcalfe, P., Beven, K.J., Freer, J. (2015) : Dynamic TOPMODEL: A new implementation in R and its sensitivity to time and space steps ; 41p. ; disponible sur semanticscholar.org
Pour en savoir plus :
- Obled, C., Zin, I. (2004) : TOPMODEL : principes de fonctionnement et application ; La houille blanche ; N°1 ; pp 65-77.
 S'abonner à un flux RSS
S'abonner à un flux RSS