Streeter et Phelps (Modèle de) (HU) : Différence entre versions
(→Formulation du modèle) |
|||
| Ligne 7 : | Ligne 7 : | ||
==Formulation du modèle== | ==Formulation du modèle== | ||
| − | Le modèle se présente sous la forme d'une équation différentielle composée d'un terme de désoxygénation (considérant la demande en oxygène pour la dégradation de la matière organique) et d'un terme d'échange gazeux avec l'atmosphère (réoxygénation si déficit par rapport à la saturation, désoxygénation si excès par rapport à la saturation) (1). Ce modèle permet en particulier de déterminer le déficit en oxygène <math>DO</math> (mg/L) par la relation : | + | Le modèle se présente sous la forme d'une équation différentielle composée d'un terme de désoxygénation (considérant la demande en oxygène pour la dégradation de la matière organique) et d'un terme d'échange gazeux avec l'atmosphère (réoxygénation si déficit par rapport à la saturation, désoxygénation si excès par rapport à la saturation) (1) (Streeter et Phelps, 1925). Ce modèle permet en particulier de déterminer le déficit en oxygène <math>DO</math> (mg/L) par la relation : |
| Ligne 23 : | Ligne 23 : | ||
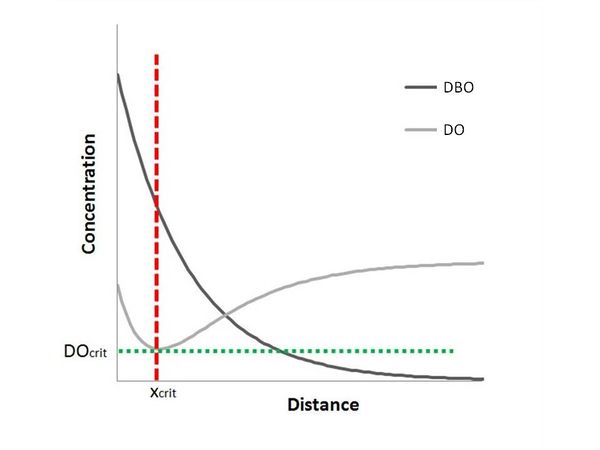
[[File:courbe_en_sac.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Représentation graphique de l'évolution de la teneur en oxygène en fonction de la distance après un point de rejet d'après l'équation de Streeter et Phelps (courbe en sac) ; <u>Source</u> : [https://en.wikipedia.org/wiki/Streeter%E2%80%93Phelps_equation Article wikipédia]''.</center>]] | [[File:courbe_en_sac.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Représentation graphique de l'évolution de la teneur en oxygène en fonction de la distance après un point de rejet d'après l'équation de Streeter et Phelps (courbe en sac) ; <u>Source</u> : [https://en.wikipedia.org/wiki/Streeter%E2%80%93Phelps_equation Article wikipédia]''.</center>]] | ||
| − | <u>Pour en savoir plus</u> : [https://en.wikipedia.org/wiki/Streeter%E2%80%93Phelps_equation Article wikipédia]. | + | |
| + | <u>Bibliographie</u> : | ||
| + | * Streeter, H.W., Phelps, E.B. (1925) : ''A Study of the pollution and natural purification of the Ohio river. III. Factors concerned in the phenomena of oxidation and reaeration'' ; Public Health Bulletin no. 146, Reprinted by U.S. Department of Health, Education and Welfare, Public Health Service, 1958, ISBN B001BP4GZI ; disponible sur : http://dspace.udel.edu:8080/dspace/bitstream/handle/19716/1590/C%26EE148.pdf?sequence=2 | ||
| + | |||
| + | <u>Pour en savoir plus</u> : | ||
| + | * [https://en.wikipedia.org/wiki/Streeter%E2%80%93Phelps_equation Article wikipédia]. | ||
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
Version du 27 septembre 2022 à 14:53
Traduction anglaise : Streeter et Phelps model
Dernière mise à jour : 24/01/2022
Le modèle de Streeter et Phelps est traditionnellement utilisé pour décrire l'évolution de la concentration en oxygène dissous et de la demande biochimique en oxygène dans une rivière, à l'aval d'un rejet.
Formulation du modèle
Le modèle se présente sous la forme d'une équation différentielle composée d'un terme de désoxygénation (considérant la demande en oxygène pour la dégradation de la matière organique) et d'un terme d'échange gazeux avec l'atmosphère (réoxygénation si déficit par rapport à la saturation, désoxygénation si excès par rapport à la saturation) (1) (Streeter et Phelps, 1925). Ce modèle permet en particulier de déterminer le déficit en oxygène $ DO $ (mg/L) par la relation :
Avec :
- $ k_1 $ : coefficient de dégradation de la matière organique ;
- $ k_2 $ : coefficient de réoxygénation de la rivière à l'interface eau/air ;
- $ L_0 $ : concentration initiale en DBO (mg/L) ;
- $ t $ : temps ;
- $ DO_0 $ : déficit initial en oxygène.
Bibliographie :
- Streeter, H.W., Phelps, E.B. (1925) : A Study of the pollution and natural purification of the Ohio river. III. Factors concerned in the phenomena of oxidation and reaeration ; Public Health Bulletin no. 146, Reprinted by U.S. Department of Health, Education and Welfare, Public Health Service, 1958, ISBN B001BP4GZI ; disponible sur : http://dspace.udel.edu:8080/dspace/bitstream/handle/19716/1590/C%26EE148.pdf?sequence=2
Pour en savoir plus :
 S'abonner à un flux RSS
S'abonner à un flux RSS