Fruhling (coefficient d'abattement de) (HU) : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Fruhling areal reduction coefficient'' | ''<u>Traduction anglaise</u> : Fruhling areal reduction coefficient'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 16/11/2022 |
Modèle permettant d'appliquer un [[Abattement spatial (HU)|abattement spatial]] aux précipitations pour tenir compte de l’hétérogénéité de leur répartition spatiale. | Modèle permettant d'appliquer un [[Abattement spatial (HU)|abattement spatial]] aux précipitations pour tenir compte de l’hétérogénéité de leur répartition spatiale. | ||
| − | |||
==Formulation mathématique== | ==Formulation mathématique== | ||
| − | La méthode de Fruhling consiste à appliquer une diminution exponentielle de l'intensité de pluie lorsque l'on s'éloigne du point où elle est maximum, appelé [[Epicentre (HU)|épicentre]] par analogie avec les tremblements de terre. L'intensité <math>i (d)</math> à une distance <math>d</math> de l'épicentre se calcule en fonction de l'intensité <math>i_0</math> sous l'épicentre par la relation : | + | La méthode de Fruhling consiste à appliquer une diminution exponentielle de l'intensité de pluie lorsque l'on s'éloigne du point où elle est maximum, appelé [[Epicentre (HU)|épicentre]] par analogie avec les tremblements de terre (''figure 1''). L'intensité <math>i (d)</math> à une distance <math>d</math> de l'épicentre se calcule en fonction de l'intensité <math>i_0</math> sous l'épicentre par la relation : |
| Ligne 18 : | Ligne 17 : | ||
Le paramètre <math>a</math> est un coefficient numérique empirique dépendant de la forme du bassin versant. Par exemple : | Le paramètre <math>a</math> est un coefficient numérique empirique dépendant de la forme du bassin versant. Par exemple : | ||
| − | |||
* <math>a</math> ≈ 0,0060 pour des bassins versants allongés (avec <math>d</math> en mètres) ; | * <math>a</math> ≈ 0,0060 pour des bassins versants allongés (avec <math>d</math> en mètres) ; | ||
* <math>a</math> ≈ 0,0052 pour des bassins versants compacts (avec <math>d</math> en mètres). | * <math>a</math> ≈ 0,0052 pour des bassins versants compacts (avec <math>d</math> en mètres). | ||
| + | |||
| + | |||
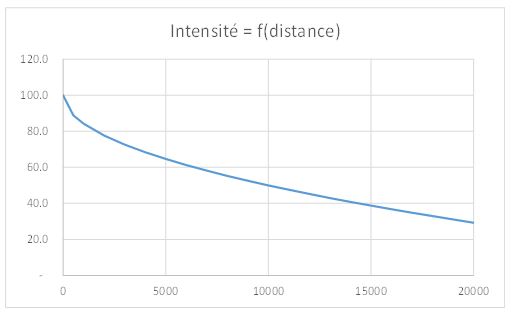
| + | [[File:fruhling.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Évolution de l'intensité en fonction de la distance à l'épicentre en utilisant la formule de Fruhling (Base 100 à l'épicentre).''</center>]] | ||
==Critique de la méthode== | ==Critique de la méthode== | ||
| − | Cette vision très simple de la structure des pluies est très éloignée de la répartition réelle instantanée des intensités ou de celle de leurs cumuls. Ces répartitions dépendent en effet de deux types d'éléments : | + | Cette vision très simple de la structure des pluies est très éloignée de la répartition réelle instantanée des intensités ou de celle de leurs cumuls (''figure 2''). Ces répartitions dépendent en effet de deux types d'éléments : |
* le développement et l'évolution temporelle et spatiale (dans les trois dimensions) des masses d'air, qui dépendent de phénomènes se mettant en place depuis les échelles régionales jusqu'aux échelles continentales ; | * le développement et l'évolution temporelle et spatiale (dans les trois dimensions) des masses d'air, qui dépendent de phénomènes se mettant en place depuis les échelles régionales jusqu'aux échelles continentales ; | ||
| − | * les éléments locaux (relief, exposition et albédo des surfaces, etc.) qui vont venir modifier les précipitations à des échelles kilométriques | + | * les éléments locaux (relief, exposition et albédo des surfaces, etc.) qui vont venir modifier les précipitations à des échelles kilométriques. |
Version du 16 novembre 2022 à 18:05
Traduction anglaise : Fruhling areal reduction coefficient
Dernière mise à jour : 16/11/2022
Modèle permettant d'appliquer un abattement spatial aux précipitations pour tenir compte de l’hétérogénéité de leur répartition spatiale.
Formulation mathématique
La méthode de Fruhling consiste à appliquer une diminution exponentielle de l'intensité de pluie lorsque l'on s'éloigne du point où elle est maximum, appelé épicentre par analogie avec les tremblements de terre (figure 1). L'intensité $ i (d) $ à une distance $ d $ de l'épicentre se calcule en fonction de l'intensité $ i_0 $ sous l'épicentre par la relation :
Le paramètre $ a $ est un coefficient numérique empirique dépendant de la forme du bassin versant. Par exemple :
- $ a $ ≈ 0,0060 pour des bassins versants allongés (avec $ d $ en mètres) ;
- $ a $ ≈ 0,0052 pour des bassins versants compacts (avec $ d $ en mètres).
Critique de la méthode
Cette vision très simple de la structure des pluies est très éloignée de la répartition réelle instantanée des intensités ou de celle de leurs cumuls (figure 2). Ces répartitions dépendent en effet de deux types d'éléments :
- le développement et l'évolution temporelle et spatiale (dans les trois dimensions) des masses d'air, qui dépendent de phénomènes se mettant en place depuis les échelles régionales jusqu'aux échelles continentales ;
- les éléments locaux (relief, exposition et albédo des surfaces, etc.) qui vont venir modifier les précipitations à des échelles kilométriques.

Cette méthode doit donc être utilisée avec beaucoup de précautions.
Voir : Abattement spatial (HU), Répartition spatio-temporelle des précipitations.
 S'abonner à un flux RSS
S'abonner à un flux RSS