Contrainte critique d’entrainement (HU) : Différence entre versions

Version du 1 octobre 2023 à 16:54

Traduction anglaise : Critical tractive stress

Dernière mise à jour : 01/10/2023

Contrainte de cisaillement critique à partir de laquelle une particule solide posée au fond est mise en mouvement par un fluide ; on parle également de seuil de cisaillement.

Formulation mathématique

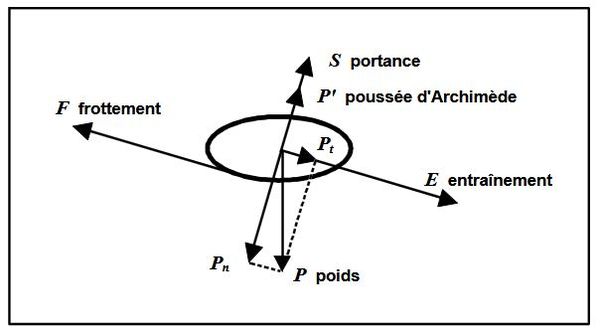
Cette contrainte peut en théorie être déterminée en écrivant le bilan des forces qui s'appliquent sur une particule solide posée au fond (Degoutte (), voir figure 1).

Figure 1 : Équilibre des forces s'exerçant sur une particule solide posée sur le fond d'un canal soumis à un écoulement ; Source : Degoutte ().

Avec :

• $ P $ : poids de la particule ;
• $ E $ : force d'entrainement exercée par le fluide ;
• $ F $ : force de frottement entre la particule et le fond :
• $ P' $ : poussée d’Archimède due à la différence de masse volumique entre la particule et le fluide ;
• $ S $ : force de portance due à la différence de vitesse d'écoulement du fluide entre la partie haute et la partie basse de la particule.

Pour calculer la contrainte critique d'entraînement, on décompose ces différentes forces selon des directions parallèle et orthogonale au fond (par exemple $ P_n $ et $ P_t $) ; on en déduit la résultante des forces et on obtient la contrainte critique de cisaillement en divisant par la surface de la particule en contact avec le fond.

Dans la pratique beaucoup de ces forces sont dépendantes de la forme de la particule, le plus souvent très irrégulière, ce qui conduit à utiliser des modèles empiriques, le plus connu étant le critère de Shields.

Pour en savoir plus :

• Degoutte, J. (non daté) : Transport solide en hydraulique fluviale ; chapitre 2 ; 22p. ; disponible sur https://vicoin.portail-bassins-versants.fr/IMG/pdf/transport_solide_en_hydraulique_fluviale.pdf

Voir aussi : Diagramme de Shields (HU).