Vitesse d'un écoulement (HU) : Différence entre versions

Version actuelle en date du 3 juillet 2024 à 12:05

Traduction anglaise : Flow velocity

Dernière mise à jour : 03/10/2023

La vitesse représente la distance parcourue par un mobile par unité de temps.

En hydraulique, on s'intéresse plus particulièrement à la vitesse moyenne de la masse de fluide dans le sens de l'écoulement ; cette vitesse correspond au rapport du débit moyen à la section de l'écoulement.

Sommaire

1 Notions de base
2 Importance et maitrise des vitesses des écoulements
3 Mesure de la vitesse

[modifier] Notions de base

[modifier] Vitesse d'une particule et vitesse d'un écoulement

S'il est facile de donner une définition théorique de la vitesse d'une particule d'eau (dérivée du déplacement par rapport au temps), il est beaucoup plus difficile de définir la vitesse d'un écoulement en tant que tel (voir Débitmétrie).

Dans un écoulement turbulent (ce qui représente la quasi-totalité des cas dans le domaine de l’assainissement), chaque particule d'eau se déplace en effet selon sa propre trajectoire en interférant en permanence avec les particules voisines, ceci selon les trois dimensions de l'espace. Dans cet article on s'intéressera spécifiquement à la composante de ce vecteur vitesse dans la direction générale de l'écoulement.

Nota : En hydraulique on s'intéresse cependant parfois aux autres composantes, par exemple pour étudier la décantation ou le débit déversé au dessus d'un seuil latéral.

[modifier] Vitesse en un point, vitesse moyenne et vitesse maximum

Les calculs en régime turbulent font intervenir deux composantes de la vitesse d’une particule liquide : une composante « vitesse moyenne » et une composante « vitesse aléatoire » dont la moyenne est nulle. Pour la pratique courante en hydrologie urbaine et en assainissement, ce niveau de description n'est généralement pas jugé nécessaire. Les calculs sont simplifiés en raisonnant uniquement sur des grandeurs moyennes, et en général unidimensionnelles, suivant l’axe principal d’écoulement. L'hypothèse la plus fréquente consiste à admettre que tous les filets liquides se déplacent à une même vitesse, parallèlement au fond et à l’axe de l’ouvrage, en particulier des conduites.

Cette hypothèse est cependant assez grossière. En effet, même dans le cas d'un régime uniforme, on sait depuis les travaux de H. Bazin (1829-1917) que la valeur de la composante longitudinale moyenne de la vitesse varie en fonction de la position dans la section transversale (voir figure 1). Par ailleurs, les vitesses transversales et les courants secondaires, que l'on peut mettre en évidence en laboratoire ou plus difficilement sur site, compliquent sérieusement toute détermination exhaustive des champs de vitesse dans un écoulement, même s'il est uniforme.

Figure 1 : Exemple de distribution des vitesses longitudinales pour un écoulement à surface libre dans un canal trapézoïdal.

Des relations entre vitesse moyenne, vitesse en un point donné et vitesse maximale ont été recherchées par de nombreux auteurs depuis le XVIIIème siècle. A titre d'exemple, les travaux de Darcy (1803-1858) repris par Bazin (1829-1917) [Darcy & Bazin, 1865] conduisent à la relation suivante pour un écoulement à surface libre en canal [Nordon, 1992] :

$ V-v = K\sqrt{R_h.I}(\dfrac{h}{H}) ^2 \qquad (1) $

Avec :

$ H $ : profondeur de l'écoulement (m) ;
$ I $ : pente du canal (m/m) ;
$ K $ : coefficient dépendant des parois ;
$ R_h $ : rayon hydraulique (m) ;
$ v $ : vitesse à la profondeur h (m/s) ;
$ V $ : vitesse maximum (Darcy) ou vitesse à la surface (Bazin) (m/s).

Une relation voisine existe pour un écoulement en conduite circulaire pleine :

$ V-v = K\sqrt{R.I}(\dfrac{r}{R}) ^3 \qquad (2) $

Avec :

$ R $ : rayon de la conduite ;
$ r $ : distance à partir du centre.

La répartition verticale des vitesses varie de manière importante en fonction des conditions hydrauliques et géométriques de l'écoulement. La figure 2 en donne quelques exemples pour des profils observés dans des cours d'eau.

Figure 2 : Exemples de profils de vitesse observés en rivières, d’après [Roche, 1963]

[modifier] Évolution de la vitesse près du fond ou des parois

Un cas particulier est la détermination du profil de vitesse à proximité immédiate du fond ou des parois (pour des distances inférieures à 2 ou 3 fois la hauteur des aspérités), qui joue en particulier un rôle dans le transport solide de fond. Von Karman a montré que dans un écoulement turbulent sur fond fixe rugueux, le profil des vitesses était logarithmique (figure 3 et relation (3)) :

Figure 3 : Profil de vitesse théorique (logarithmique) au voisinage d'un fond fixe en cas d'écoulement turbulent.

$ \frac{u}{u_*} = \frac{1}{K}ln{\frac{h}{h_0}}+B_s\qquad(3) $

avec :

$ K $ : constante de Von Karman (sans dimension), dont la valeur est comprise entre 0,36 et 0,42 (normalement 0,41) ;
$ u $ : vitesse moyenne du fluide à la hauteur $ h $ (m/s) ;
$ h_0 $ : hauteur de rugosité (hauteur assimilée à celle pour laquelle $ u $ devient nulle) (m) ;
$ h $ : hauteur dans la veine liquide (m) ;
$ u_* $ : vitesse de frottement (m/s) ;
$ B_s $ : constante d'intégration fonction du nombre de Reynolds et dont la valeur est comprise entre 6 et 10 selon le type d'écoulement (sans dimension).

[modifier] Importance et maitrise des vitesses des écoulements

La vitesse des écoulements joue un rôle important en assainissement :

si elle est trop forte, les risques d'érosion des conduites augmentent et le pouvoir d'entraînement de l'eau peut même devenir dangereux en cas de débit important ;
si elle est trop faible, la capacité de transport solide de l'écoulement est insuffisante, et les conditions d'autocurage ne peuvent plus être respectées.

On a donc intérêt à choisir la forme des conduites d'assainissement de façon à obtenir une vitesse aussi indépendante que possible du débit et du remplissage. C'est en particulier pour cette raison qu’a été souvent préconisée l'utilisation de conduites ovoïdes. La figure 4 donne, à titre indicatif les courbes d'évolution de la vitesse et du débit en fonction de la hauteur pour une conduite circulaire et pour une conduite ovoïde.

Figure 4 : Évolution de la vitesse moyenne d'écoulement et du débit en fonction de la hauteur de remplissage pour des conduites circulaires et ovoïdes.

[modifier] Mesure de la vitesse

La mesure de la vitesse des écoulements est importante à plusieurs titres, et notamment pour déterminer les débits, variable essentielle, avec le niveau d’eau, pour décrire les écoulements, et permettant aussi d’évaluer directement des volumes, à stocker ou rejetés. Différentes techniques de mesure existent, en association avec des mesures de hauteur pour déterminer les sections d'écoulement.

Certaines de ces mesures sont mises en œuvre de façon limitée dans le temps (jaugeage) pour obtenir une relation hauteur-vitesse supposée stable et permettant de calculer le débit en mesurant de façon continue uniquement la vitesse.
D'autres sont mises en œuvre de façon continue en même temps que les mesures de hauteur, ce qui permet de détecter des phénomènes parasites comme par exemple des influences aval.

[modifier] Mesure au moulinet ou au micro-moulinet

Principes de la méthode : On mesure la vitesse de rotation d'une hélice mobile placée dans l'écoulement et on en déduit la vitesse de l'eau à son voisinage par une relation de proportionnalité (figure 5).

Figure 5 : Mesure de la vitesse de l'écoulement au micromoulinet ; Source : Mesures de débit

[modifier] Mesure du temps de transit par ultrasons

Principes de la méthode : On place deux sondes face à face, alignées suivant une droite parallèle à la pente du fond et biaise par rapport à l’axe principal (voir figure 6) et on compare le temps mis par l'onde dans le sens amont-aval (la vitesse de l'eau s'ajoute à la vitesse de l'onde) avec le temps mis par l'onde pour aller dans le sens aval-amont (la vitesse de l'eau se retranche à la vitesse de l'onde)

Figure 6 : Schéma de principe d'une corde de mesure de la vitesse.

[modifier] Mesure par effet Doppler

Principe de la méthode : On envoie une onde ultrasonore dans le sens de l'écoulement, cette onde se réfléchit sur les particules présentes dans l'eau et on meure le changement de longueur d'onde entre l'onde émise et l'onde réfléchie. La sonde peut être aérienne (dans ce cas on mesure la vitesse en surface) ou immergée (dans ce cas on mesure une pseudo vitesse moyenne des particules présentes dans l'écoulement.

partie de l'article en chantier

Bibliographie :

Darcy H. & Bazin H. (1865) : Recherches hydrauliques entreprises par M.H. Darcy, continuées par M. H. Bazin ; Librairie des Corps impériaux des Ponts et chaussées et des mines ; Dunod ; MDCCCLXV.
Nordon M. (1991) : Histoire de l'hydraulique. Tome 1 : L'eau conquise - les origines et le monde antique ; Tome 2 : L'eau démontrée - du Moyen-Age à nos jours. ; Ed. Masson ; Paris ; 181 p et 242 p. ; 1991 et 1992.
Roche, M. (1963) : Hydrologie de Surface ; ed. Gauthier-Villars ; Paris ; 430 pp.

@@ Ligne 1 : / Ligne 1 : @@
-''<u>Traduction anglaise : </u>Flow velocity''
+''<u>Traduction anglaise</u> : Flow velocity''
-La vitesse représente la distance parcourue par un mobile par unité de temps. En hydraulique on s'intéresse plus particulièrement à la vitesse moyenne des écoulements, rapport du débit sur la section d'écoulement.
+<u>Dernière mise à jour</u> : 03/10/2023
-== Notions de base ==
+La vitesse représente la distance parcourue par un mobile par unité de temps.
-S'il est facile de donner une définition théorique de la vitesse d'une particule d'eau (dérivée du déplacement par rapport au temps), il est beaucoup plus difficile de définir la vitesse d'un écoulement en tant que tel (voir [[Débitmétrie (HU)|Débitmétrie]]).
+En hydraulique, on s'intéresse plus particulièrement à la vitesse moyenne de la masse de fluide dans le sens de l'écoulement ; cette vitesse correspond au rapport du débit moyen à la section de l'écoulement.
-Dans un [[Ecoulement turbulent (HU)|écoulement turbulent]] (ce qui représente la quasi-totalité des cas dans le domaine de l’assainissement), chaque particule d'eau se déplace en effet selon sa propre trajectoire en interférant en permanence avec les particules voisines, selon les trois dimensions de l'espace. Les calculs en régime turbulent font intervenir deux composantes de la vitesse d’une particule liquide : une composante « vitesse moyenne » et une composante « vitesse aléatoire » dont la moyenne est nulle. Pour la pratique courante en hydrologie urbaine et en assainissement, ce niveau de description n'est généralement pas jugé nécessaire. Les calculs sont simplifiés en raisonnant uniquement sur des grandeurs moyennes, et en général unidimensionnelles, suivant l’axe principal d’écoulement. L'hypothèse la plus fréquente consiste à admettre que tous les filets liquides se déplacent à une même vitesse, parallèlement au fond et à l’axe de l’ouvrage, en particulier des conduites.
-Cette hypothèse est cependant assez grossière. En effet, même dans le cas d'un régime [[Ecoulement uniforme (HU)|uniforme]], on sait depuis les travaux de H. Bazin (1829-1917) que la valeur de la composante longitudinale moyenne de la vitesse varie en fonction de la position dans la section transversale (voir figure 1). Par ailleurs, les vitesses transversales et les courants secondaires, que l'on peut mettre en évidence en laboratoire ou plus difficilement sur site, complique sérieusement toute détermination exhaustive des champs de vitesse dans un écoulement, même s'il est uniforme.
+== Notions de base ==
+===Vitesse d'une particule et vitesse d'un écoulement===
+S'il est facile de donner une définition théorique de la vitesse d'une particule d'eau (dérivée du déplacement par rapport au temps), il est beaucoup plus difficile de définir la vitesse d'un écoulement en tant que tel (voir [[Débitmétrie (HU)|Débitmétrie]]).
-<center>[[Fichier:DEHUA208.png]]
+Dans un [[Ecoulement turbulent (HU)|écoulement turbulent]] (ce qui représente la quasi-totalité des cas dans le domaine de l’assainissement), chaque particule d'eau se déplace en effet selon sa propre trajectoire en interférant en permanence avec les particules voisines, ceci selon les trois dimensions de l'espace. Dans cet article on s'intéressera spécifiquement à la composante de ce vecteur vitesse dans la direction générale de l'écoulement.
-''Figure 1 : Exemple de distribution des vitesses longitudinales pour un écoulement à surface libre dans un canal trapézoïdal''
+<u>Nota</u> : En hydraulique on s'intéresse cependant parfois aux autres composantes, par exemple pour étudier la décantation ou le débit déversé au dessus d'un seuil latéral.
-</center>
-Des relations entre vitesse moyenne, vitesse en un point donné et vitesse maximale ont été recherchées par de nombreux auteurs depuis le
+===Vitesse en un point,  vitesse moyenne et vitesse maximum===
-ème siècle. A titre d'exemple, les travaux de Darcy (1803-1858) repris par Bazin (1829-1917) [Darcy & Bazin, 1865] conduisent à la relation suivante
-pour un écoulement à surface libre en canal [Nordon, 1992] :
-<math>V-v = K\sqrt{R_hI}(\dfrac{h}{H})^2</math>
+Les calculs en régime turbulent font intervenir deux composantes de la vitesse d’une particule liquide : une composante « vitesse moyenne » et une composante « vitesse aléatoire » dont la moyenne est nulle. Pour la pratique courante en hydrologie urbaine et en assainissement, ce niveau de description n'est généralement pas jugé nécessaire. Les calculs sont simplifiés en raisonnant uniquement sur des grandeurs moyennes, et en général unidimensionnelles, suivant l’axe principal d’écoulement. L'hypothèse la plus fréquente consiste à admettre que tous les filets liquides se déplacent à une même vitesse, parallèlement au fond et à l’axe de l’ouvrage, en particulier des conduites.
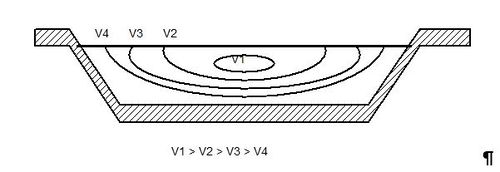
-<center>[[Fichier:DEHUA209.png]]</center>
+Cette hypothèse est cependant assez grossière. En effet, même dans le cas d'un régime [[Ecoulement uniforme (HU)|uniforme]], on sait depuis les travaux de H. Bazin (1829-1917) que la valeur de la composante longitudinale moyenne de la vitesse varie en fonction de la position dans la section transversale (voir ''figure 1''). Par ailleurs, les vitesses transversales et les courants secondaires, que l'on peut mettre en évidence en laboratoire ou plus difficilement sur site, compliquent sérieusement toute détermination exhaustive des champs de vitesse dans un écoulement, même s'il est uniforme.
-Avec :
-·    H   :     profondeur de l'écoulement (m) ;
+[[File:vitesse1.JPG|500px|center|thumb|<center>''<u>Figure 1</u> : Exemple de distribution des vitesses longitudinales pour un écoulement à surface libre dans un canal trapézoïdal.''</center>]]
-·    I     :     pente du canal (m/m) ;
+Des relations entre vitesse moyenne, vitesse en un point donné et vitesse maximale ont été recherchées par de nombreux auteurs depuis le XVIIIème siècle. A titre d'exemple, les travaux de Darcy (1803-1858) repris par Bazin (1829-1917) [Darcy & Bazin, 1865] conduisent à la relation suivante pour un écoulement à surface libre en canal [Nordon, 1992] :
-·    K    :     coefficient dépendant des parois ;
-·    Rh  :     rayon hydraulique (m) ;
+<center><math>V-v = K\sqrt{R_h.I}(\dfrac{h}{H}) ^2 \qquad (1)</math></center>
-·    v    :     vitesse à la profondeur h (m/s) ;
+Avec :
+* <math>H</math>   : profondeur de l'écoulement (m) ;
+* <math>I</math>   : pente du canal (m/m) ;
+* <math>K</math>   : coefficient dépendant des parois ;
+* <math>R_h</math> : rayon hydraulique (m) ;
+* <math>v</math>   : vitesse à la profondeur h (m/s) ;
+* <math>V</math>   : vitesse maximum (Darcy) ou vitesse à la surface (Bazin) (m/s).
-·    V    :     vitesse maximum (Darcy) ou vitesse à la surface (Bazin) (m/s).
+Une relation voisine existe pour un écoulement en conduite circulaire pleine :
+<center><math>V-v = K\sqrt{R.I}(\dfrac{r}{R}) ^3 \qquad (2)</math></center>
-Une relation voisine existe pour un écoulement en conduite circulaire pleine :
+Avec :
+* <math>R</math>   : rayon de la conduite ;
+* <math>r</math>   : distance à partir du centre.
-<math>V-v = K\sqrt{RI}(\dfrac{r}{R})^3</math>
+La répartition verticale des vitesses varie de manière importante en fonction des conditions hydrauliques et géométriques de l'écoulement. La ''figure 2'' en donne quelques exemples pour des profils observés dans des cours d'eau.
-<center>[[Fichier:DEHUA210.png]]</center>
-Avec :
+[[File:vitesse2.JPG|800px|center|thumb|<center>''<u>Figure 2</u> : Exemples de profils de vitesse observés en rivières, d’après [Roche, 1963]''</center>]]
-·     R   :     rayon de la conduite ;
+===Évolution de la vitesse près du fond ou des parois===
-·     r    :     distance à partir du centre.
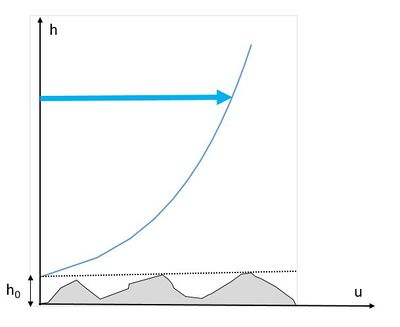
+Un cas particulier est la détermination du profil de vitesse à proximité immédiate du fond ou des parois (pour des distances inférieures à 2 ou 3 fois la hauteur des aspérités), qui joue en particulier un rôle dans le [[Transport solide de fond (HU)|transport solide de fond]]. Von Karman a montré que dans un [[Ecoulement turbulent (HU)|écoulement turbulent]] sur fond fixe rugueux, le profil des vitesses était logarithmique (''figure 3'' et relation (3)) :
-La répartition verticale des vitesses varie de manière importante en fonction des conditions hydrauliques et géométriques de
-l'écoulement. La figure 2 en donne quelques exemples pour des profils observés dans des cours d'eau.
+[[File:von_karman_profil_vitesse.JPG|400px|center|thumb|<center>''Figure 3 : Profil de vitesse théorique (logarithmique) au voisinage d'un fond fixe en cas d'écoulement turbulent.''</center>]]
-<center>
-{| class="wikitable"
-|-
+<center><math>\frac{u}{u_*} = \frac{1}{K}ln{\frac{h}{h_0}}+B_s\qquad(3)</math></center>
-|style="text-align: center;"| [[Fichier:DEHUA211.png]]
+avec :
-|style="text-align: center;"| [[Fichier:DEHUA212.png]]
+* <math>K</math> : [[Von Karman (constante de) (HU)|constante de Von Karman]] (sans dimension), dont la valeur est comprise entre 0,36 et 0,42 (normalement 0,41) ;
-|style="text-align: center;"| [[Fichier:DEHUA213.png]]
+* <math>u</math> : vitesse moyenne du fluide à la hauteur <math>h</math> (m/s) ;
-|style="text-align: center;"| [[Fichier:DEHUA214.png]]
+* <math>h_0</math> : hauteur de rugosité (hauteur assimilée à celle pour laquelle <math>u</math> devient nulle) (m) ;
+* <math>h</math> : hauteur dans la veine liquide (m) ;
+* <math>u_*</math> : [[Vitesse de frottement (HU)|vitesse de frottement]] (m/s) ;
+* <math>B_s</math> : constante d'intégration fonction du [[Nombre de Reynolds (HU)|nombre de Reynolds]] et dont la valeur est comprise entre 6 et 10 selon le type d'écoulement (sans dimension).
-|-
+== Importance et maitrise des vitesses des écoulements ==
-|style="text-align: center;"| Grandes vitesses,
+La vitesse des écoulements joue un rôle important en assainissement :
-écoulement très turbulent.
+* si elle est trop forte, les risques d'érosion des conduites augmentent et le pouvoir d'entraînement de l'eau peut même devenir dangereux en cas de débit important ;
-|style="text-align: center;"| Faibles vitesses, fond lisse.
+* si elle est trop faible, la capacité de transport solide de l'écoulement est insuffisante, et les conditions [[Autocurage (HU)|d'autocurage]] ne peuvent plus être respectées.
-|style="text-align: center;"| Fond rugueux, rochers.
-|style="text-align: center;"| fond très rugueux, végétation aquatique
-importante.
-|-
+On a donc intérêt à choisir la forme des conduites d'assainissement de façon à obtenir une vitesse aussi indépendante que possible du débit et du remplissage. C'est en particulier pour cette raison qu’a été souvent préconisée l'utilisation de conduites ovoïdes. La ''figure 4'' donne, à titre indicatif les courbes d'évolution de la vitesse et du débit en fonction de la hauteur pour une conduite circulaire et pour une conduite [[Ovoïde (HU)|ovoïde]].
-|style="text-align: center;"| [[Fichier:DEHUA215.png]]
-|style="text-align: center;"| [[Fichier:DEHUA216.png]]
-|style="text-align: center;"| [[Fichier:DEHUA217.png]]
-|-
+[[File:vitesse3.JPG|600px|center|thumb|<center><u>Figure 4</u> : Évolution de la vitesse moyenne d'écoulement et du débit en fonction de la hauteur de remplissage pour des conduites circulaires et ovoïdes.</center>]]
-|style="text-align: center;"| courbe des vitesses au dessus d’un bourrelet,
-d’un rocher important, etc.
-|style="text-align: center;"| courbe des vitesses au dessus d’un bourrelet,
-d’un trou, à l’aval d’un rocher, etc.
-|style="text-align: center;"| freinage en surface (branches immergées, etc.).
-|}
+== Mesure de la vitesse ==
+La mesure de la vitesse des écoulements est importante à plusieurs titres, et notamment pour déterminer les débits, variable essentielle, avec le niveau d’eau, pour décrire les écoulements, et permettant aussi d’évaluer directement des volumes, à stocker ou rejetés. Différentes techniques de mesure existent, en association avec des mesures de hauteur pour déterminer les sections d'écoulement.
+* Certaines de ces mesures sont mises en œuvre de façon limitée dans le temps ([[Jaugeage (HU)|jaugeage]]) pour obtenir une relation hauteur-vitesse supposée stable et permettant de calculer le débit en mesurant de façon continue uniquement la vitesse.
+* D'autres sont mises en œuvre de façon continue en même temps que les mesures de hauteur, ce qui permet de détecter des phénomènes parasites comme par exemple des [[Influence aval (HU)|influences aval]].
-''Figure 2 : Exemples de profils de vitesse observés en rivières, d’après [Roche, 1963]''
+===Mesure au moulinet ou au micro-moulinet===
-</center>
-== Importance et maitrise des vitesses des écoulements ==
+<u>Principes de la méthode</u> : On mesure la vitesse de rotation d'une hélice mobile placée dans l'écoulement et on en déduit la vitesse de l'eau à son voisinage par une relation de proportionnalité (''figure 5'').
-La vitesse des écoulements joue un rôle important en assainissement :
-·
+[[File:moulinet.JPG|600px|center|thumb|<center>''<u>Figure 5</u> : Mesure de la vitesse de l'écoulement au micromoulinet ; <u>Source</u> : [[Mesures de débit]]''</center>]]
-si elle est trop forte, les risques d'érosion des conduites augmentent et le pouvoir d'entraînement de l'eau peut même devenir dangereux en cas de
-débit important ;
-·
+===Mesure du temps de transit par ultrasons===
-si elle est trop faible, la capacité de transport solide de l'écoulement est insuffisante, et les conditions [[Autocurage (HU)|d'autocurage]]
-ne peuvent plus être respectées.
-On a donc intérêt à choisir la forme des conduites d'assainissement de façon à obtenir une vitesse aussi indépendante que possible du débit et du remplissage. C'est en particulier pour cette raison qu’a été souvent préconisée l'utilisation de conduites ovoïdes. La figure 3 donne, à titre indicatif les courbes d'évolution de la vitesse et du débit en fonction de la hauteur pour une conduite circulaire et pour une conduite [[Ovoïde (HU)|ovoïde]].
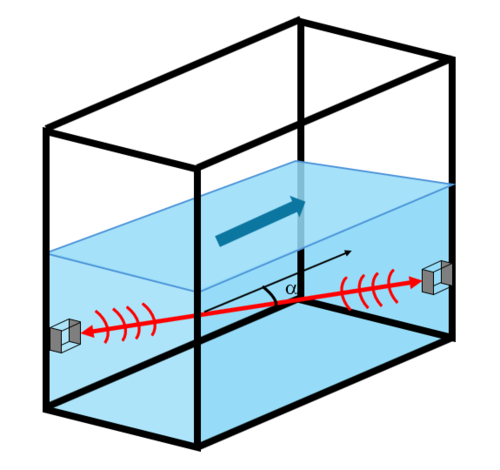
+<u>Principes de la méthode</u> : On place deux sondes face à face, alignées suivant une droite parallèle à la pente du fond et biaise par rapport à l’axe principal (voir ''figure 6'') et on compare le temps mis par l'onde dans le sens amont-aval (la vitesse de l'eau s'ajoute à la vitesse de l'onde) avec le temps mis par l'onde pour aller dans le sens aval-amont (la vitesse de l'eau se retranche à la vitesse de l'onde)
-<center>[[Fichier:DEHUA218.png]]
+[[File:velocimètre_corde_ultra_son.PNG|500px|center|thumb|<center>''<u>Figure 6</u> : Schéma de principe d'une corde de mesure de la vitesse.''</center>]]
-Vitesse en fonction du remplissage pour une canalisation circulaire.
+===Mesure par effet Doppler===
+Principe de la méthode : On envoie une onde ultrasonore dans le sens de l'écoulement, cette onde se réfléchit sur les particules présentes dans l'eau et on meure le changement de longueur d'onde entre l'onde émise et l'onde réfléchie. La sonde peut être aérienne (dans ce cas on mesure la vitesse en surface) ou immergée (dans ce cas on mesure une pseudo vitesse moyenne des particules présentes dans l'écoulement.
-[[Fichier:DEHUA219.png]]
-Vitesse en fonction du remplissage pour une canalisation ovoïde.
-''Figure 3 : Evolution de la vitesse moyenne d'écoulement et du débit en fonction de la hauteur de remplissage pour des conduites circulaires et ovoïdes.''
-</center>
-== Mesure de la vitesse ==
-La mesure de la vitesse des écoulements est importante à plusieurs titres, et notamment pour déterminer les débits, variable essentielle,
+''partie de l'article en chantier''
-avec le niveau d’eau, pour décrire les écoulements, et permettant aussi d’évaluer directement des volumes, à stocker ou rejetés. Différentes techniques
-de mesure existent, en association avec des mesures de hauteur pour déterminer les sections d'écoulement.
-Voir [[Débitmétrie (HU)|Débitmétrie]].
+<u>Bibliographie</u> :
+* Darcy H. & Bazin H. (1865) : Recherches hydrauliques entreprises par M.H. Darcy, continuées par M. H. Bazin ; Librairie des Corps impériaux des Ponts et chaussées et des mines ; Dunod ; MDCCCLXV.
+* Nordon M. (1991) : Histoire de l'hydraulique. Tome 1 : L'eau conquise - les origines et le monde antique ; Tome 2 : L'eau démontrée - du Moyen-Age à nos jours. ; Ed. Masson ; Paris ; 181 p et 242 p. ; 1991 et 1992.
+* Roche, M. (1963) : Hydrologie de Surface ; ed. Gauthier-Villars ; Paris ; 430 pp.
 [[Catégorie:Dictionnaire_DEHUA]]
+[[Catégorie:Processus_de_base_et_hydraulique_des_réseaux_(HU)]]