Fractal (HU) : Différence entre versions
(→Dimension fractale d'un bassin versant) |
|||
| (4 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Fractal'' | ''<u>Traduction anglaise</u> : Fractal'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 03/03/2025 |
| − | Néologisme créé par le mathématicien B.Mandelbrot pour désigner certains objets rugueux ou lacunaires | + | Néologisme créé par le mathématicien B.Mandelbrot (voir par exemple Mandelebrot, 1980) pour désigner certains objets rugueux ou lacunaires qui présentent une structure similaire à toutes les échelles (''figure 1''). |
| − | La notion de [[Dimension fractale (HU)|dimension fractale]] est utilisée en hydrologie dans | + | ==Généralités== |
| + | |||
| + | La dimension associée à ce type d'objet ([[Dimension fractale (HU)|dimension fractale]]) a la propriété de ne pas être entière. Par exemple la "dimension fractale" de la côte de Bretagne n'est pas une longueur exprimable en mètres mais est intermédiaire entre une longueur et une surface. | ||
| + | |||
| + | |||
| + | [[File:fractal_mandelbrot.JPG|400px|center|thumb|<center>''<u>Figure 1</u> : Exemple d'ensemble de Mandelbrot ; <u>Source</u> : https://fr.wikipedia.org/wiki/Fractale.''</center>]] | ||
| + | |||
| + | ==Intérêt en hydrologie urbaine== | ||
| + | |||
| + | La notion de [[Dimension fractale (HU)|dimension fractale]] est utilisée en hydrologie dans différents domaines ; par exemple : | ||
* pour caractériser les champs de pluie ; | * pour caractériser les champs de pluie ; | ||
* pour analyser le comportement hydrologique des bassins versants. | * pour analyser le comportement hydrologique des bassins versants. | ||
| − | ==Modèle fractal de précipitation== | + | ===Modèle fractal de précipitation=== |
Le météorologue canadien Lovejoy (1983) a proposé dans les années 1980, de considérer que la structure temporelle et spatiale des précipitations suivait une loi de variation telle qu'il serait possible de considérer les précipitations comme des objets fractals. La méthode utilisée est la suivante : | Le météorologue canadien Lovejoy (1983) a proposé dans les années 1980, de considérer que la structure temporelle et spatiale des précipitations suivait une loi de variation telle qu'il serait possible de considérer les précipitations comme des objets fractals. La méthode utilisée est la suivante : | ||
| Ligne 18 : | Ligne 27 : | ||
Ceci signifie que la surface considérée dépend de l'échelle à laquelle on la considère et que cette dépendance est en puissance <math>C(s)</math> de <math>L</math> avec <math>C(s) = 2 - D(s)</math>. <math>D(s)</math> est appelée [[Dimension fractale (HU)|dimension fractale]]. <math>C(s)</math> est appelée co-dimension fractale. Si <math>D(s)</math> varie lorsque <math>s</math> varie, le phénomène est dit multifractal. C'est le cas de la pluie. | Ceci signifie que la surface considérée dépend de l'échelle à laquelle on la considère et que cette dépendance est en puissance <math>C(s)</math> de <math>L</math> avec <math>C(s) = 2 - D(s)</math>. <math>D(s)</math> est appelée [[Dimension fractale (HU)|dimension fractale]]. <math>C(s)</math> est appelée co-dimension fractale. Si <math>D(s)</math> varie lorsque <math>s</math> varie, le phénomène est dit multifractal. C'est le cas de la pluie. | ||
| − | ==Dimension fractale d'un bassin versant== | + | ===Dimension fractale d'un bassin versant=== |
| − | La théorie de la dimension fractale peut également être appliquée pour modéliser l'organisation des bassins versants à partir des lignes de drainage. Cette approche est plus facile à mettre en œuvre dans le cas des réseaux d'assainissement pour lesquels il est facile de connaître la structure. Elle permet de rendre compte de la complexité morphologique des réseaux, qu'ils soient ramifiés ou non | + | La théorie de la dimension fractale peut également être appliquée pour modéliser l'organisation des bassins versants à partir des lignes de drainage. Cette approche est plus facile à mettre en œuvre dans le cas des réseaux d'assainissement pour lesquels il est facile de connaître la structure. Elle permet de rendre compte de la complexité morphologique des réseaux, qu'ils soient ramifiés ou non, et de donner un sens plus précis à certains paramètres hydrologiques ([[Lag time (HU)|lag time]] en particulier) (Thibault, 1987). Réméniéras (1976) indique par exemple "''(cette approche) est sans doute susceptible d'asseoir la modélisation des bassins versants sur des paramètres dont la signification physique sera indiscutable''" . |
| − | En faisant appel à la théorie de la dimension fractale, la technique | + | En faisant appel à la théorie de la dimension fractale, la technique d'analyse de l'organisation des réseaux d'assainissement revient à vérifier si numériquement leur développement spatial à partir de l'exutoire est suffisamment bien approximé par un modèle de la forme : |
<center><math>C(u) = a.u^D</math></center> | <center><math>C(u) = a.u^D</math></center> | ||
| − | |||
avec : | avec : | ||
* <math>u</math> : valeur du rayon d'un cercle centré sur l'exutoire ; | * <math>u</math> : valeur du rayon d'un cercle centré sur l'exutoire ; | ||
* <math>C(u)</math> : longueur caractéristique du réseau contenu dans le cercle, mesurée avec la même unité que <math>u</math>. | * <math>C(u)</math> : longueur caractéristique du réseau contenu dans le cercle, mesurée avec la même unité que <math>u</math>. | ||
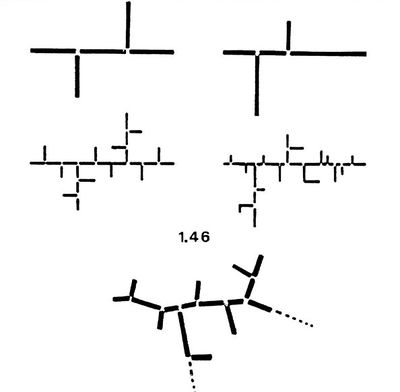
| − | <math>D</math> est alors la dimension (non entière en règle générale) du réseau considéré que l'on peut appeler dimension de contenu (Thibault, 1987). | + | <math>D</math> est alors la dimension (non entière en règle générale) du réseau considéré que l'on peut appeler dimension de contenu (Thibault, 1987). Elle varie de 1 pour un réseau linéaire à 2 pour un réseau totalement développé qui couvrirait la totalité de l'espace de façon homogène (''figure 2''). |
| − | [[File:fractal.JPG|400px|center|thumb|<center>''<u>Figure | + | [[File:fractal.JPG|400px|center|thumb|<center>''<u>Figure 2</u> : Exemple d'analyse fractale d'un réseau d’assainissement ; <u>Source</u> : Thibault (1991)''</center>]] |
<u>Bibliographie</u> : | <u>Bibliographie</u> : | ||
* Lovejoy, S (1983) : La géométrie fractale des régions de pluie et les simulations aléatoires ; La houille blanche ; n°5/6 ; pp 431-436. | * Lovejoy, S (1983) : La géométrie fractale des régions de pluie et les simulations aléatoires ; La houille blanche ; n°5/6 ; pp 431-436. | ||
| + | * Mandelbrot, B. (1980) : ''Fractal aspects of the iteration of z -> λ.z.(1-z) for complex λ'' ; Annals NY Acad. Sci. ; vol. 357, 1980, p. 249/259. | ||
* Réméniéras, G. (1976) : L'hydrologie de l'ingénieur ; Paris, Eyrolles ; 251 p. | * Réméniéras, G. (1976) : L'hydrologie de l'ingénieur ; Paris, Eyrolles ; 251 p. | ||
* Thibault, S. (1987) : modélisation morphofonctionnelle des réseaux d'assainissement à l'aide du concept de dimension fractale ; Thèse d'état INSA. Lyon ; 303 p. | * Thibault, S. (1987) : modélisation morphofonctionnelle des réseaux d'assainissement à l'aide du concept de dimension fractale ; Thèse d'état INSA. Lyon ; 303 p. | ||
Version actuelle en date du 3 mars 2025 à 09:28
Traduction anglaise : Fractal
Dernière mise à jour : 03/03/2025
Néologisme créé par le mathématicien B.Mandelbrot (voir par exemple Mandelebrot, 1980) pour désigner certains objets rugueux ou lacunaires qui présentent une structure similaire à toutes les échelles (figure 1).
Sommaire |
[modifier] Généralités
La dimension associée à ce type d'objet (dimension fractale) a la propriété de ne pas être entière. Par exemple la "dimension fractale" de la côte de Bretagne n'est pas une longueur exprimable en mètres mais est intermédiaire entre une longueur et une surface.

[modifier] Intérêt en hydrologie urbaine
La notion de dimension fractale est utilisée en hydrologie dans différents domaines ; par exemple :
- pour caractériser les champs de pluie ;
- pour analyser le comportement hydrologique des bassins versants.
[modifier] Modèle fractal de précipitation
Le météorologue canadien Lovejoy (1983) a proposé dans les années 1980, de considérer que la structure temporelle et spatiale des précipitations suivait une loi de variation telle qu'il serait possible de considérer les précipitations comme des objets fractals. La méthode utilisée est la suivante :
- on appelle $ S_s(L) $ la surface couverte par des intensités de pluie dépassant le seuil $ s $ ; on évalue cette surface en comptabilisant le nombre $ N(L) $ de pixels élémentaires de taille $ L.L $ où cette intensité est dépassée ;
- on écrit cette surface sous la forme d'une fonction de $ L $ : $ S_s(L) = N(L) . L^2 $ ;
- l'analyse de données radar pour une gamme de valeurs de $ L $ montre que $ N(L) $ est proportionnel à $ L^{2-D(s)} $ avec $ D(s) $ différent de $ 2 $.
Ceci signifie que la surface considérée dépend de l'échelle à laquelle on la considère et que cette dépendance est en puissance $ C(s) $ de $ L $ avec $ C(s) = 2 - D(s) $. $ D(s) $ est appelée dimension fractale. $ C(s) $ est appelée co-dimension fractale. Si $ D(s) $ varie lorsque $ s $ varie, le phénomène est dit multifractal. C'est le cas de la pluie.
[modifier] Dimension fractale d'un bassin versant
La théorie de la dimension fractale peut également être appliquée pour modéliser l'organisation des bassins versants à partir des lignes de drainage. Cette approche est plus facile à mettre en œuvre dans le cas des réseaux d'assainissement pour lesquels il est facile de connaître la structure. Elle permet de rendre compte de la complexité morphologique des réseaux, qu'ils soient ramifiés ou non, et de donner un sens plus précis à certains paramètres hydrologiques (lag time en particulier) (Thibault, 1987). Réméniéras (1976) indique par exemple "(cette approche) est sans doute susceptible d'asseoir la modélisation des bassins versants sur des paramètres dont la signification physique sera indiscutable" .
En faisant appel à la théorie de la dimension fractale, la technique d'analyse de l'organisation des réseaux d'assainissement revient à vérifier si numériquement leur développement spatial à partir de l'exutoire est suffisamment bien approximé par un modèle de la forme :
avec :
- $ u $ : valeur du rayon d'un cercle centré sur l'exutoire ;
- $ C(u) $ : longueur caractéristique du réseau contenu dans le cercle, mesurée avec la même unité que $ u $.
$ D $ est alors la dimension (non entière en règle générale) du réseau considéré que l'on peut appeler dimension de contenu (Thibault, 1987). Elle varie de 1 pour un réseau linéaire à 2 pour un réseau totalement développé qui couvrirait la totalité de l'espace de façon homogène (figure 2).
Bibliographie :
- Lovejoy, S (1983) : La géométrie fractale des régions de pluie et les simulations aléatoires ; La houille blanche ; n°5/6 ; pp 431-436.
- Mandelbrot, B. (1980) : Fractal aspects of the iteration of z -> λ.z.(1-z) for complex λ ; Annals NY Acad. Sci. ; vol. 357, 1980, p. 249/259.
- Réméniéras, G. (1976) : L'hydrologie de l'ingénieur ; Paris, Eyrolles ; 251 p.
- Thibault, S. (1987) : modélisation morphofonctionnelle des réseaux d'assainissement à l'aide du concept de dimension fractale ; Thèse d'état INSA. Lyon ; 303 p.
- Thibault, S. (1991) : Fractals et structure des réseaux urbains d’assainissement eau pluviale. Flux - Cahiers scientifiques internationaux Réseaux et territoires, Metropolis / Université Paris-Est Marne la Vallée, pp.5-14. téléchargeable sur https://hal.archives-ouvertes.fr/hal-00654988/document
 S'abonner à un flux RSS
S'abonner à un flux RSS