Distribution granulométrique (HU) : Différence entre versions
(→Importance de la distribution granulométrique des particules présentes dans un écoulement) |
|||
| (Une révision intermédiaire par un utilisateur est masquée) | |||
| Ligne 1 : | Ligne 1 : | ||
| + | [[File:logo_eurydice.jpg|80px]][[File:Logo OFB_soutien financier.png|120px]] | ||
| + | |||
''<u>Traduction anglaise</u> : Grain size distribution'' | ''<u>Traduction anglaise</u> : Grain size distribution'' | ||
| Ligne 29 : | Ligne 31 : | ||
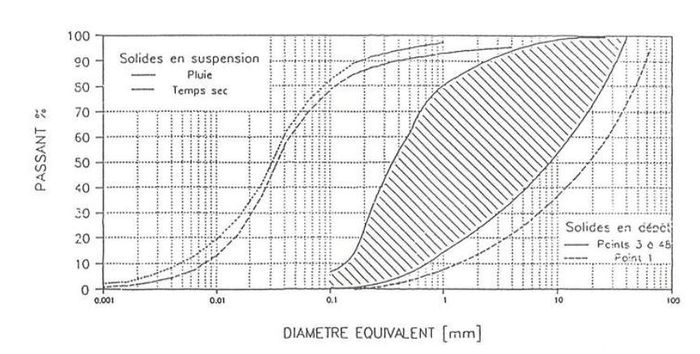
| − | [[File:granulometrie.JPG|700px|center|thumb|<center>''<u>Figure 1</u> : | + | [[File:granulometrie.JPG|700px|center|thumb|<center>''<u>Figure 1</u> : Distribution granulométrique des solides en suspension et solides des dépôts dans le collecteur 13 de MARSEILLE ; <u>Source</u> : Laplace (1991).''</center>]] |
| − | On caractérise souvent la | + | On caractérise souvent la distribution granulométrique par la taille médiane <math>d50</math> qui est telle que 50% des particules (en masse) ont une taille inférieure et 50% une taille supérieure. Il est également possible d'utiliser d'autres quantiles, par exemple <math>d10</math>, telle que 10% des particules (en masse) ont une taille inférieure et 90% une taille supérieure. |
<u>Nota</u> : on assimile parfois la taille à un diamètre moyen ou équivalent. Cette équivalence n'est vraie que dans le cas de particules sensiblement sphériques. Dans le cas général de particules de formes quelconques, la méthode de mesure (tamisage) provoque un tri des particules en fonction de leur plus petite dimension. | <u>Nota</u> : on assimile parfois la taille à un diamètre moyen ou équivalent. Cette équivalence n'est vraie que dans le cas de particules sensiblement sphériques. Dans le cas général de particules de formes quelconques, la méthode de mesure (tamisage) provoque un tri des particules en fonction de leur plus petite dimension. | ||
Version actuelle en date du 26 juin 2025 à 09:52
Traduction anglaise : Grain size distribution
Dernière mise à jour : 05/03/2025
Distribution en masse, en volume, parfois en nombre, des particules solides contenues dans un milieu donné en fonction de leur taille ; on parle parfois simplement de granulométrie, même si ce dernier terme devrait être réservé à l'étude de la distribution granulométrique et non à son résultat.
Nota : En hydrologie urbaine on utilise principalement la distribution en masse.
[modifier] Utilisation de la notion en hydrologie et en assainissement
En hydrologie et dans les domaines connexes (génie civil, travaux publics), ce terme est utilisé dans différents contextes :
- pour qualifier la distribution des particules transportées par l'écoulement ou déposées dans le réseau ;
- pour qualifier un sol ;
- pour expliciter la taille des granulats à utiliser pour un usage donné (par exemple un remblai ou une structure poreuse) ; dans ce sens une granulométrie 20/40 désigne un matériau dont la dimension des grains est comprise entre 20 et 40 mm.
[modifier] Importance de la distribution granulométrique des particules présentes dans un écoulement
La distribution granulométrique des particules joue en particulier un rôle dans leur aptitude à fixer les polluants. Elle joue également un rôle dans leur vitesse de décantation, donc dans la capacité de transport solide d'un écoulement.
Cette notion est donc importante vis à vis de différentes problématiques de gestion :
- risque d'ensablement des réseaux ;
- capacité de décantation des ouvrages de traitement ;
- évaluation des risques de rejets polluants ;
- etc.
[modifier] Méthode de mesure
La distribution granulométrique est généralement déterminée en passant l'échantillon au travers de tamis de taille décroissante et en pesant les particules retenues. Les résultats sont généralement reportés sur une courbe représentant la distribution fréquentielle cumulée (figure 1).
On caractérise souvent la distribution granulométrique par la taille médiane $ d50 $ qui est telle que 50% des particules (en masse) ont une taille inférieure et 50% une taille supérieure. Il est également possible d'utiliser d'autres quantiles, par exemple $ d10 $, telle que 10% des particules (en masse) ont une taille inférieure et 90% une taille supérieure.
Nota : on assimile parfois la taille à un diamètre moyen ou équivalent. Cette équivalence n'est vraie que dans le cas de particules sensiblement sphériques. Dans le cas général de particules de formes quelconques, la méthode de mesure (tamisage) provoque un tri des particules en fonction de leur plus petite dimension.
Il n'est pas toujours facile de donner un sens très clair à la distribution granulométrique des particules organiques transportées dans les réseaux d'assainissement. Celles-ci peuvent en effet se désagréger facilement ou au contraire former des flocs. Pour connaître la décantabilité des particules transportées il est préférable d'étudier la distribution des valeurs des vitesses de chute.
Bibliographie :
- Laplace, D (1991) : Dynamique du dépôt en collecteur d'assainissement ; thèse de Doctorat de l'INP de Toulouse, Spécialité de Mécanique des Fluides ; 202p. + annexes ; disponible sur http://www.theses.fr/1991INPT002H.
 S'abonner à un flux RSS
S'abonner à un flux RSS