Bernoulli (théorème de) (HU) : Différence entre versions
De Wikhydro
| (5 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Bernoulli's equation'' | ''<u>Traduction anglaise</u> : Bernoulli's equation'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 27/06/2025 |
Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et [[Ecoulement permanent (HU)|permanent]]. | Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et [[Ecoulement permanent (HU)|permanent]]. | ||
| − | ==Formulation | + | ==Formulation mathématique== |
| − | + | ||
| − | + | ||
| + | La relation de Bernoulli s'écrit, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2 - voir ''figure 1''), sous la forme suivante : | ||
| Ligne 16 : | Ligne 15 : | ||
Avec : | Avec : | ||
* <math>V</math> : vitesse (m/s) ; | * <math>V</math> : vitesse (m/s) ; | ||
| − | * <math>p</math> : pression (pression | + | * <math>p</math> : pression (pression totale ou pression relative si on néglige la pression atmosphérique) (Pa) ; |
* <math>h</math> : hauteur d'eau (m) ; | * <math>h</math> : hauteur d'eau (m) ; | ||
* <math>ρ</math> : masse volumique (kg/m<sup>3</sup>) ; | * <math>ρ</math> : masse volumique (kg/m<sup>3</sup>) ; | ||
* <math>g</math> : accélération de la pesanteur (m/s<sup>2</sup>) ; | * <math>g</math> : accélération de la pesanteur (m/s<sup>2</sup>) ; | ||
* <math>z</math> : altitude (m) ; | * <math>z</math> : altitude (m) ; | ||
| − | * <math>Δh</math> : pertes de charge dues aux frottements sur les parois et à la [[Viscosité (HU)|viscosité]] entre les sections 1 et 2 ( | + | * <math>Δh</math> : pertes de charge dues aux frottements sur les parois et à la [[Viscosité (HU)|viscosité]] entre les sections 1 et 2 (m). |
Dans cette expression, l'énergie est exprimée en hauteur de fluide. Voir [[Charge hydraulique (HU)|Charge hydraulique]]. | Dans cette expression, l'énergie est exprimée en hauteur de fluide. Voir [[Charge hydraulique (HU)|Charge hydraulique]]. | ||
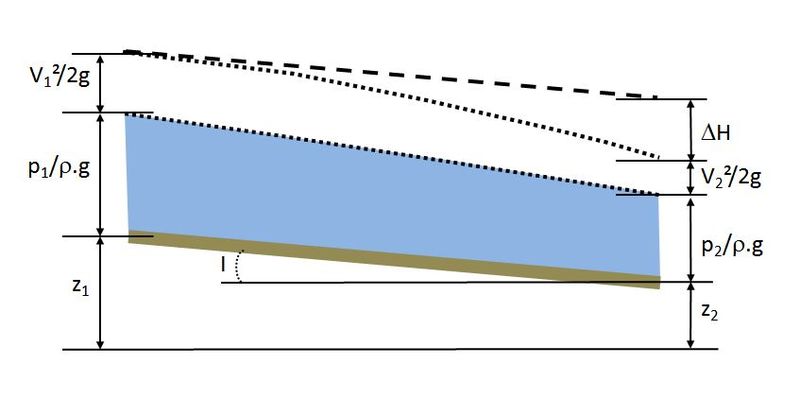
| − | [[File: | + | [[File:bernoulli1.JPG|800px|center|thumb|<center>''<u>Figure 1</u> : Représentation des différentes grandeurs dans l'équation de Bernoulli dans le cas d'un écoulement à surface libre ; on raisonne en pression relative et on ne prend pas en compte la pression atmosphérique.''</center>]] |
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
[[Catégorie:Processus_de_base_et_hydraulique_des_réseaux_(HU)]] | [[Catégorie:Processus_de_base_et_hydraulique_des_réseaux_(HU)]] | ||
[[Catégorie:Modélisation_des_écoulements_en_réseau_et_en_rivière_(HU)]] | [[Catégorie:Modélisation_des_écoulements_en_réseau_et_en_rivière_(HU)]] | ||
Version actuelle en date du 27 juin 2025 à 20:16
Traduction anglaise : Bernoulli's equation
Dernière mise à jour : 27/06/2025
Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et permanent.
[modifier] Formulation mathématique
La relation de Bernoulli s'écrit, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2 - voir figure 1), sous la forme suivante :
Avec :
- $ V $ : vitesse (m/s) ;
- $ p $ : pression (pression totale ou pression relative si on néglige la pression atmosphérique) (Pa) ;
- $ h $ : hauteur d'eau (m) ;
- $ ρ $ : masse volumique (kg/m3) ;
- $ g $ : accélération de la pesanteur (m/s2) ;
- $ z $ : altitude (m) ;
- $ Δh $ : pertes de charge dues aux frottements sur les parois et à la viscosité entre les sections 1 et 2 (m).
Dans cette expression, l'énergie est exprimée en hauteur de fluide. Voir Charge hydraulique.
 S'abonner à un flux RSS
S'abonner à un flux RSS