Utilisateur:Jean-Michel Tanguy/SujetENTPE2023/PRADES BRUNEAU DELOUS : Différence entre versions
(→Solution par homotopie) |
(→Solution analytique) |
||
| (112 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | |||
| − | |||
| − | + | ==Contexte== | |
| + | Au cours du XX<sup>ème</sup> siècle le niveau moyen des mers s'est élevé de 18 cm et d'ici 2100, en France, le niveau pourrait s'élever en moyenne de 50 à 100cm dans le plus pessimiste des cas à cause du réchauffement climatique.[1] En conséquence, l'érosion côtière se retrouve amplifiée et près d'un tiers du littoral français se retrouve concerné. Cela représente un véritable problème pour les milieux naturels et les populations concernées (20 % de la population mondiale et 10 % de celle française réside à moins de 30km du littoral).[2] Pour quantifier et prévoir les impacts de ces phénomènes, il est possible de modéliser différents types de houle. | ||
| − | + | [[File:erosion1.jpg|500px|Erosion sur le littoral Atlantique]] | |
| − | |||
| − | + | Ainsi notre étude porte sur les houles et leur impact sur le littoral. Afin de les étudier nous partirons du modèle de Berkhoff et nous utiliserons la méthode par homotopie pour résoudre les équations des différents cas que nous étudierons. Nous les comparerons ensuite aux solutions analytiques de façon graphique pour attester de l'efficacité de la méthode. | |
| − | |||
| + | Lien de la vidéo illustratrice de notre sujet : | ||
| + | https://youtu.be/H_ZsmYrNXQM | ||
| + | |||
| + | == Modèle de Berkhoff == | ||
| + | Ce modèle a pour expression (en bi-dimensionnel): | ||
| + | |||
| + | <math> \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 </math> | ||
| + | |||
| + | où <math> \phi</math> est le potentiel, k est le nombre d’onde fonction de la profondeur H et de la fréquence <math>\omega </math> (T est la période), par la relation implicite <math> \omega^2=gk \tanh(kH)</math> , C est la célérité de l’onde, Cg est la célérité de groupe des vagues. | ||
| + | |||
| + | Pour simplifier le problème, nous nous placerons dans le domaine des ondes longues, ce qui signifie que <math> C=C_g=\sqrt{gH}</math>. | ||
| + | |||
| + | L'évolution dans le temps de la hauteur de houle est donnée par : <math>h(x,t)=\Re \left (\phi e^{-i\omega t} \right ) </math>. | ||
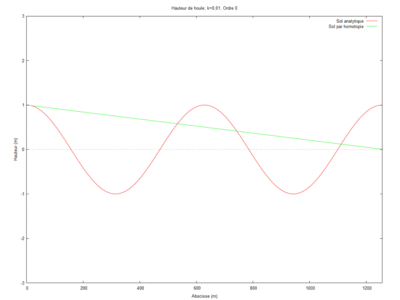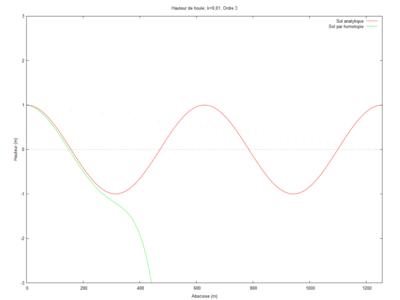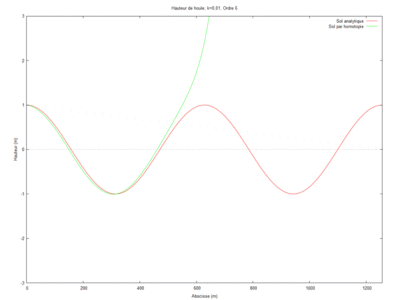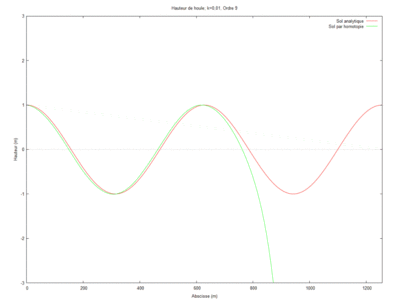
== Cas n°1 : == | == Cas n°1 : == | ||
| + | |||
| + | Canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire <math> \phi=1</math> (condition de Dirichlet) et sortie libre amont <math> \phi_x=ik\phi</math> (condition de Robin). | ||
| + | |||
=== Solution analytique === | === Solution analytique === | ||
| Ligne 54 : | Ligne 67 : | ||
Ainsi on a <math display="block"> \phi(x) = e^{ikx} = \cos(kx) + i\sin(kx)</math> | Ainsi on a <math display="block"> \phi(x) = e^{ikx} = \cos(kx) + i\sin(kx)</math> | ||
| + | === Solution par homotopie === | ||
| + | |||
| + | ==== Ordre 0 ==== | ||
| + | |||
| + | <math>\phi_{0,xx}=0</math> soit <math>\phi_0=Ax+B</math>. | ||
| + | |||
| + | En introduisant les conditions limites suivantes: <math>\phi_0^0=1</math> et <math>\phi_{0,x}^L=ik\phi_{0}^L</math>, il vient : | ||
| + | |||
| + | <math>\phi_0=1+\dfrac{ik}{1-ikL}x</math>. | ||
| + | |||
| + | ==== Ordre 1 ==== | ||
| + | |||
| + | <math>\phi_{1,xx}-\phi_{0,xx}+\phi_{0,xx}+k^2\phi_0=0</math> soit <math>\phi_{1}=-k^2\int\phi_0dxdx +Ax+B</math>. | ||
| + | |||
| + | En introduisant les conditions limites suivantes: <math>\phi_1^0=0</math> et <math>\phi_{1,x}^L=ik\phi_{1}^L</math>, | ||
| + | il vient : <math>\phi_1=- \dfrac{k^2L(k^2L^2+3ikL-3} {3(1-ikL)^2}x-k^2\left (\dfrac{ik} {6(1-ikL)}x^3+\dfrac{1} {2}x^2 \right )</math> | ||
| − | === | + | ==== Ordre 2 ==== |
En réutilisant la décomposition par série entière, on arrive pour l'ordre 2 à : | En réutilisant la décomposition par série entière, on arrive pour l'ordre 2 à : | ||
| Ligne 74 : | Ligne 103 : | ||
<math> \phi_{2} = k^2\left[ \frac{-k^2L \left(k^2L^2+3ikL-3\right)x^3}{18\left(1-ikL\right)^2} - k^2\left(\frac{ikx^5}{120\left(1-ikL\right)} + \frac{x^4}{24} \right) \right] + x^3 \left[\frac{-k^4L\left(k^2L^2 + 3ikL -3\right)}{6\left(1-ikL\right)^3}\right] + x^4 \left[\frac{-3k^2\left(1-ikL\right)^3 + ik^5L \left(k^2L^2+3ikL-3\right)}{18\left(1-ikl\right)^3} \right] + x^5 \left[\frac{k^2\left(1-ikL\right)^3 - ik^3}{24\left(1-ikL\right)^2}\right]-\frac{x^5k^3i}{120\left(1-ikL\right)^2} + \frac{ik}{1-ikL} + 1 </math>. | <math> \phi_{2} = k^2\left[ \frac{-k^2L \left(k^2L^2+3ikL-3\right)x^3}{18\left(1-ikL\right)^2} - k^2\left(\frac{ikx^5}{120\left(1-ikL\right)} + \frac{x^4}{24} \right) \right] + x^3 \left[\frac{-k^4L\left(k^2L^2 + 3ikL -3\right)}{6\left(1-ikL\right)^3}\right] + x^4 \left[\frac{-3k^2\left(1-ikL\right)^3 + ik^5L \left(k^2L^2+3ikL-3\right)}{18\left(1-ikl\right)^3} \right] + x^5 \left[\frac{k^2\left(1-ikL\right)^3 - ik^3}{24\left(1-ikL\right)^2}\right]-\frac{x^5k^3i}{120\left(1-ikL\right)^2} + \frac{ik}{1-ikL} + 1 </math>. | ||
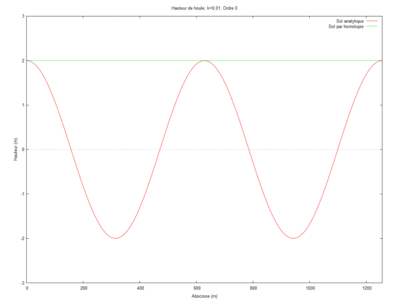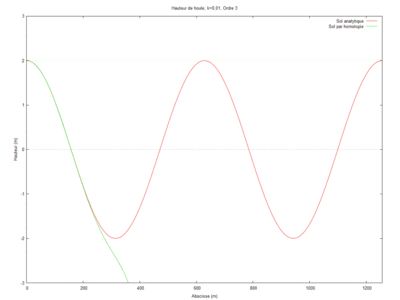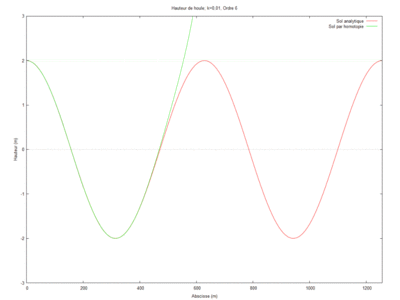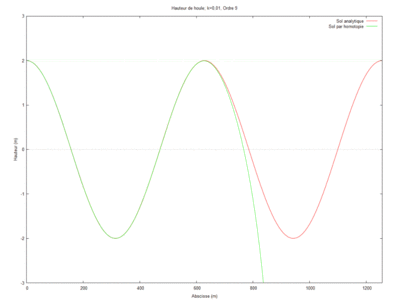
| + | [[File:Cas 1.gif|400px]] | ||
== Cas n°2 : == | == Cas n°2 : == | ||
| + | |||
| + | Domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval | ||
| + | <math> \phi_x=ik(2-\phi)</math> et réflexion totale amont <math> \phi_x=0</math> | ||
=== Solution analytique : === | === Solution analytique : === | ||
| Ligne 90 : | Ligne 123 : | ||
Cela équivaut à <math display="block">B\cdot e^{-ikL} = e^{ikL}</math>. D'où <math display="block">B= e^{2ikL}</math>. | Cela équivaut à <math display="block">B\cdot e^{-ikL} = e^{ikL}</math>. D'où <math display="block">B= e^{2ikL}</math>. | ||
| + | |||
| + | Ainsi, <math display="block"> \phi(x) = e^{ikx}(1 + e^{2ik(L-x)}) </math> | ||
===Solution par homotopie : === | ===Solution par homotopie : === | ||
| − | Ordre 2 : | + | ==== Ordre 0 : ==== |
| + | |||
| + | Le développement de l'expression donne à l'ordre 0 : | ||
| + | |||
| + | <math> \phi_{0,xx}=0 \Rightarrow \phi_{0}(x)=Ax+B </math> | ||
| + | |||
| + | La première condition initiale donne : <math> \phi_{0,x}^L=0 \Rightarrow \phi_{0}(x)=B </math > | ||
| + | |||
| + | Le deuxième donne <math> \phi_{0,x}^0=ik(2-\phi_{0}^0) \Rightarrow B=2 </math> | ||
| + | |||
| + | Ainsi <math> \phi_{0}(x)=2 </math> | ||
| + | |||
| + | ==== Ordre 1 : ==== | ||
| + | <math> \phi_1(x)=-k^2\int\phi_0(x)dxdx+Ax+B</math> d'où: <math> \phi_{1,x}(x)=-k^2\int\phi_0(x)dx+A</math> | ||
| + | |||
| + | Condition limite en x=0 : | ||
| + | * <math> \phi_{1,x}(x=0)=-ik \phi_{1}(x=0)</math> soit <math>\left|-k^2\int\phi_0(x)dx+A\right|_{x=0}=ik\left|-k^2\int\phi_0(x)dxdx+Ax+B\right|_{x=0}==>A=-ikB</math> | ||
| + | |||
| + | Condition limite en x=L : | ||
| + | * <math> \phi_{1,x}(x=L)=0</math> soit <math>\left|-k^2\int\phi_0(x)dx+A\right|_{x=L}=0 ==>A=k^2\int\phi_0(x)dx==>A=2k^2L</math> | ||
| + | |||
| + | on en déduit: <math> \phi_1(x)=-k^2x^2+2k^2Lx+2ikL </math> | ||
| + | |||
| + | ==== Ordre 2 : ==== | ||
On a <math> \phi_2 = k^2 \iint\phi_1 \mathrm{d}x + Ax + B </math>. | On a <math> \phi_2 = k^2 \iint\phi_1 \mathrm{d}x + Ax + B </math>. | ||
| − | Et la condition initiale en 0 donne <math> A = -ikB </math> | + | Et la condition initiale en 0 donne <math> A = -ikB </math> |
La seconde condition initiale nous donne <math> A = k^2 \int\phi_1 \mathrm{d}x </math>. | La seconde condition initiale nous donne <math> A = k^2 \int\phi_1 \mathrm{d}x </math>. | ||
| Ligne 102 : | Ligne 160 : | ||
En remplaçant les constantes dans l'expression de <math> \phi_2 </math> on obtient : | En remplaçant les constantes dans l'expression de <math> \phi_2 </math> on obtient : | ||
| − | <math> \phi_2 = \frac {k^4x^4}{12} - \frac{k^4Lx^3}{3} - ik^ | + | <math> \phi_2 = \frac {k^4x^4}{12} - \frac{k^4Lx^3}{3} - ik^3L^2 + x\frac{2}{3}k^4L^3 + 2ik^3L^2x -\frac{2}{3} ik^3L^3 + 2ik^2L^2 </math> |
| + | [[File:Cas 2.gif|400px]] | ||
== Cas n°3 : == | == Cas n°3 : == | ||
| + | Domaine monodimensionnel de longueur L avec pente du fond constante (s=cste) avec entrée par l'aval d'une onde de fréquence unitaire <math>\phi=1</math> et sortie libre amont <math>\phi_x=ik\phi</math> | ||
| + | |||
=== Solution analytique === | === Solution analytique === | ||
| + | |||
Reprenons l'équation de Berkhoff : <math display="block">\operatorname{grad}(C\cdot C_g\cdot \operatorname{grad}(\phi)) + k^2\cdot C\cdot C_g\cdot \phi = 0 </math> . On considère à présent <math display="block">C</math> et <math display="block">C_g</math> non constantes. On a donc <math display="block">\operatorname{grad}(g\cdot H\cdot \operatorname{grad}(\phi)) + k^2\cdot g\cdot H\cdot \phi = 0 </math>. Cela donne <math display="block"> g\cdot H\cdot \frac{\partial^2 \phi}{\partial x^2} -s\cdot g\cdot \frac{\partial \phi}{\partial x} + k^2\cdot g\cdot H\cdot \phi = 0 </math>. Puis on divise par g. | Reprenons l'équation de Berkhoff : <math display="block">\operatorname{grad}(C\cdot C_g\cdot \operatorname{grad}(\phi)) + k^2\cdot C\cdot C_g\cdot \phi = 0 </math> . On considère à présent <math display="block">C</math> et <math display="block">C_g</math> non constantes. On a donc <math display="block">\operatorname{grad}(g\cdot H\cdot \operatorname{grad}(\phi)) + k^2\cdot g\cdot H\cdot \phi = 0 </math>. Cela donne <math display="block"> g\cdot H\cdot \frac{\partial^2 \phi}{\partial x^2} -s\cdot g\cdot \frac{\partial \phi}{\partial x} + k^2\cdot g\cdot H\cdot \phi = 0 </math>. Puis on divise par g. | ||
| Ligne 127 : | Ligne 189 : | ||
<math display="block">\phi_x(L)=ik\phi(L) </math> | <math display="block">\phi_x(L)=ik\phi(L) </math> | ||
| − | Ainsi : <math display="block"> AJ_0(2\alpha\sqrt{H_0}) + | + | Ainsi : <math display="block"> AJ_0(2\alpha\sqrt{H_0}) + BY_0(2\alpha\sqrt{H_0})=1 </math> |
| − | Et : <math display="block"> \frac{\alpha S}{\sqrt{H_0-sL}}(AJ_1(2\alpha\sqrt{H_0-sL}) + BY_1(2\alpha\sqrt{H_0-sL}) = ik(AJ_0(2\alpha\sqrt{H_0-sL}) + BY_0(2\alpha\sqrt{H_0-sL}) </math> | + | Et : <math display="block"> \frac{\alpha S}{\sqrt{H_0-sL}}(AJ_1(2\alpha\sqrt{H_0-sL}) + BY_1(2\alpha\sqrt{H_0-sL})) = ik(AJ_0(2\alpha\sqrt{H_0-sL}) + BY_0(2\alpha\sqrt{H_0-sL})) </math> |
| + | |||
| + | On pose alors : | ||
| + | <math display="block"> Y_0^0 = Y_0(2\alpha\sqrt{H_0}) </math> | ||
| + | |||
| + | <math display="block"> J_0^0 = J_0(2\alpha\sqrt{H_0}) </math> | ||
| + | |||
| + | <math display="block"> J_0^L = J_0(2\alpha\sqrt{H_0-sL}) </math> | ||
| + | |||
| + | <math display="block"> Y_0^L = Y_0(2\alpha\sqrt{H_0-sL}) </math> | ||
| + | |||
| + | <math display="block"> J_1^L = J_1(2\alpha\sqrt{H_0-sL}) </math> | ||
| + | |||
| + | <math display="block"> Y_1^L = Y_1(2\alpha\sqrt{H_0-sL}) </math> | ||
| + | |||
| + | De plus, on remarque que <math display="block"> \frac{\alpha S}{\sqrt{H_0-sL}} = k </math>. | ||
| + | |||
| + | On a alors : <math display="block"> A=\frac{1-BY_1(2\alpha \sqrt{H_0})}{J_0(2\alpha \sqrt{H_0})} </math> | ||
| + | En remplaçant A dans la deuxième équation, on obtient alors <math display="block"> B = \frac{iJ_0^L - J_1^L}{J_0^0(Y_1^L-iY_0^L) + Y_0^0(iJ_0^L - J_1^L)}</math> | ||
| + | |||
| + | On obtient <math display="block"> A=\frac{1}{J_0^0} - \frac{(iJ_0^L - J_1^L)Y_1^0}{J_0^0(J_0^0(Y_1^L - iY_0^L) + Y_0^0(iJ_0^L - J_1^L))} </math> | ||
| + | |||
| + | Ainsi, <math display="block"> \phi(z)= (\frac{1}{J_0^0} - \frac{(iJ_0^L - J_1^L)Y_1^0}{J_0^0(J_0^0(Y_1^L - iY_0^L) + Y_0^0(iJ_0^L - J_1^L))}) J_0(2\alpha\sqrt{z}) + \frac{iJ_0^L - J_1^L} | ||
| + | {J_0^0(Y_1^L-iY_0^L) + Y_0^0(iJ_0^L - J_1^L)}Y_0(2\alpha\sqrt{z}) </math> | ||
=== Solution par homotopie === | === Solution par homotopie === | ||
Pour ce cas les conditions aux limites sont : | Pour ce cas les conditions aux limites sont : | ||
<math> \phi(0)= 1 </math> et <math> \phi_x^L=ik\phi^L </math> | <math> \phi(0)= 1 </math> et <math> \phi_x^L=ik\phi^L </math> | ||
| + | |||
| + | Cas où k est constant | ||
| + | |||
| + | On a les mêmes conditions aux limites que le cas n°1 où on a aussi <math>k=k_0</math> constant donc on retrouve les mêmes résultats que pour le cas n°1 | ||
| + | |||
| + | Cas où k est variable | ||
| + | |||
| + | On a <math> k=k_0\sqrt{\frac{H_0}{H(x)}} </math> | ||
| + | |||
| + | ==== Ordre 0 : ==== | ||
| + | |||
| + | On a <math> \phi_{0,xx} = 0 \Rightarrow \phi_0(x)=Ax+B </math> | ||
| + | |||
| + | Avec les conditions aux limites on détermine <math> B=1 </math> et <math> A(1-ik_LL) = ik_L </math> | ||
| + | |||
| + | On résout pour trouver A : <math> A=\frac{ik_L}{1-ik_LL} </math> avec <math>k_L=k_0\sqrt{\frac{H_0}{H_L}}</math> | ||
| + | |||
| + | Ce qui donne comme résultat final : <math> \phi_0(x)=\frac{ik_L}{1-ik_LL}x+1</math> | ||
| + | |||
| + | |||
| + | ==== Ordre 1 : ==== | ||
| + | |||
| + | L'équation à résoudre est : <math> (H_0-sx)\phi_{xx}-s\phi_x+k_0^2H_0\phi=0 </math> | ||
| + | |||
| + | On pose <math> \epsilon = \frac{s}{H_0}</math> | ||
| + | |||
| + | La relation d'homotopie donne ainsi : <math> \phi_{1,xx}=\epsilon\phi_{0,x}-k_0^2\phi_0 </math> | ||
| + | |||
| + | On intègre pour arriver à <math> \phi_1(x)=\epsilon\frac{ik_L}{1-ik_LL}\frac{x^2}{2}-k_0^2[\frac{x^2}{2}+\frac{ik_L}{1-ik_LL}\frac{x^3}{6}]+A_1x+B_1</math> | ||
| + | |||
| + | Avec les conditions initiales on détermine A et B : | ||
| + | |||
| + | <math> \phi_1(0)=0 \Rightarrow B_1=0 </math> | ||
| + | |||
| + | et <math> \phi_{1,x}^L=ik_L\phi_1^L \Rightarrow A_1= \frac{ik_L}{1-ik_LL}[\epsilon\frac{ik_L}{1-ik_LL}\frac{L^2}{2}-k_0^2(\frac{L^2}{2}+\frac{ik_L}{1-ik_LL}\frac{L^3}{6})]-\epsilon\frac{ik_L}{(1-ik_LL)^2}L+k_0^2[L+\frac{ik_L}{1-ik_LL}\frac{L^2}{2}] </math> | ||
| + | |||
| + | == Cas n°4 == | ||
| + | Vague sphérique générée par une source périodique sinusoïdale. | ||
| + | |||
| + | Nous traitons ici de l'évolution de la surface libre dans un domaine infini en grande profondeur. La source ponctuelle est appliquée autour d'un cercle de rayon r_0 centré sur un domaine circulaire de rayon R qui laisse sortir librement cette onde en r=R. l'équation de Berkhoff se simplifie alors en équation de Helmholtz et s'exprime en coordonnées polaires avec les conditions suivantes: | ||
| + | |||
| + | <math> \phi_{rr}+\frac{1}{r}\phi_r+k^2\phi=0</math>, <math>\phi^0=1</math>,<math> \phi^R=ik\phi_r</math> | ||
| + | |||
| + | === Solution analytique === | ||
| + | Dans le cas de l'équation de Helmholtz en coordonnées polaires pour un cercle, la forme de la solution utilisant les fonctions de Bessel est donnée par : | ||
| + | |||
| + | <math display="block">\phi(r) = [A J₀(kr) + B Y₀(kr)]</math> | ||
| + | |||
| + | On a les conditions initiales suivantes : | ||
| + | |||
| + | <math display="block"> \phi(r_0) = 1 </math> | ||
| + | |||
| + | <math display="block"> \phi_r (R) = ik\phi(R) </math> | ||
| + | |||
| + | Sachant que <math display="block"> J_0'=-J_1 </math> et <math display="block"> Y_0'=-Y_1 </math> , on obtient les deux équations suivantes : | ||
| + | |||
| + | <math display="block"> AJ_0(r_0) + BY_0(r_0) = 1 </math> | ||
| + | |||
| + | <math display="block"> -AJ_1(R) - BY_1(R) = ik(AJ_0(R) + BY_0(R))</math> | ||
| + | |||
| + | Ainsi, on obtient : | ||
| + | |||
| + | <math display="block"> A = \frac{Y_1(R)+ikY_0(R)}{-Y_0(r_0)J_1(R)+J_0(r_0)Y_1(R)-ikJ_0(R)Y_0(r_0)+ikJ_0(r_0)Y_0(R)} </math> | ||
| + | |||
| + | Et : <math display="block"> B = \frac{1}{Y_0(r_0)} - \frac{J_0(r_0)(Y_1(R)+ikY_0(R))}{Y_0(r_0)(Y_1(R)J_0(r0)+ikY_0(R)J_0(r0)−J_1(R)Y_0(r0)−ikJ_0(R)Y_1(R))} </math> | ||
| + | |||
| + | Ainsi : | ||
| + | |||
| + | <math display="block">\phi(r) = [ \frac{Y_1(R)+ikY_0(R)}{-Y_0(r_0)J_1(R)+J_0(r_0)Y_1(R)-ikJ_0(R)Y_0(r_0)+ikJ_0(r_0)Y_0(R)}J₀(kr) +(\frac{1}{Y_0(r_0)} - \frac{J_0(r_0)(Y_1(R)+ikY_0(R))}{Y_0(r_0)(Y_1(R)J_0(r0)+ikY_0(R)J_0(r0)−J_1(R)Y_0(r0)−ikJ_0(R)Y_1(R))})Y₀(kr)]</math> | ||
| + | |||
| + | === Solution par homotopie === | ||
| + | ==== Ordre 0 : ==== | ||
| + | |||
| + | On a <math display="block"> \phi_{0,rr}=0 \Rightarrow \phi_0(r)=Ar+B </math> | ||
| + | |||
| + | On utilise les conditions initiales pour déterminer A et B : | ||
| + | |||
| + | <math> \phi_0^{r_0}=1 \Rightarrow Ar_0+B=1 </math> | ||
| + | |||
| + | <math> \phi_r^{r=R}=ik\phi^{r=R} \Rightarrow A(1-ikR)=ikB </math> | ||
| + | |||
| + | |||
| + | On forme ainsi un système de deux équations et deux inconnues qui donne une fois résout : | ||
| + | |||
| + | <math> A=\frac{ik}{ik(r_0-R)+1} </math> et <math> B=1-\frac{r_0ik}{ik(r_0-R)+1}</math> | ||
| + | |||
| + | |||
| + | Ce qui donne <math>\phi_0(r)=r\frac{ik}{ik(r_0-R)+1}+1-\frac{r_0ik}{ik(r_0-R)+1} </math> | ||
| + | |||
| + | |||
| + | |||
| + | ==== Ordre 1 : ==== | ||
| + | |||
| + | On a <math>\phi_{1r,r}(r)+\frac{1}{r}\phi_{0,r}(r)+k^2\phi_0(r)=0</math> | ||
| + | |||
| + | On remplace <math> \phi_0 </math> et <math> \phi_{0,r} </math> par leur expression avec <math> A_0 = \frac{ik}{ik(r_0-R)+1} </math> et <math> B_0=1-\frac{r_0ik}{ik(r_0R)+1} </math> | ||
| + | |||
| + | <math> \Rightarrow \phi_{1,rr}=-\frac{1}{R_0}A_0-k^2(A_0r+B_0) </math> | ||
| + | |||
| + | On intègre deux fois <math> \phi_1(r)=-(rln(r)-r)A_0-k^2(A_0\frac{r^3}{6}+B_0{r^2}{2})+A_1r+B_1 </math> | ||
| + | |||
| + | On détermine <math>A_1</math> et <math>B_1</math> avec les conditions initiales : | ||
| + | |||
| + | <math>\phi_1^{r_0}=0 \Rightarrow B_1=0 </math> | ||
| + | |||
| + | <math>\phi_{1,r}^R=ik\phi_1^R \Rightarrow A_1=\frac{1}{1-ik}[[(Rln(R)-R)A_0+k^2(A_0A_0\frac{R^3}{6}+B_0\frac{R^2}{2})]ik-ln(R)A_0-k^2(A_0\frac{R^2}{2}+B_0R)]</math> | ||
| + | |||
| + | |||
| + | |||
| + | == Bibliographie == | ||
| + | [1] Milieu Marin France. « Érosion côtière ». https://www.milieumarinfrance.fr/Nos-rubriques/Etat-du-milieu/Erosion-cotiere. | ||
| + | |||
| + | [2] UP’ Magazine. « Sur les plages de l’Atlantique, l’érosion côtière révèle les lacunes juridiques françaises » https://up-magazine.info/planete/climat/85226-sur-les-plages-de-latlantique-lerosion-cotiere-revele-les-lacunes-juridiques-francaises/. | ||
| + | |||
| + | [3] Vercelot, Salomé. « Ce sont les communes les plus touchées par l’érosion du littoral en France ». Futura. https://www.futura-sciences.com/planete/actualites/environnement-ce-sont-communes-plus-touchees-erosion-littoral-france-98355/. | ||
Version actuelle en date du 14 juin 2023 à 19:56
Sommaire |
[modifier] Contexte
Au cours du XXème siècle le niveau moyen des mers s'est élevé de 18 cm et d'ici 2100, en France, le niveau pourrait s'élever en moyenne de 50 à 100cm dans le plus pessimiste des cas à cause du réchauffement climatique.[1] En conséquence, l'érosion côtière se retrouve amplifiée et près d'un tiers du littoral français se retrouve concerné. Cela représente un véritable problème pour les milieux naturels et les populations concernées (20 % de la population mondiale et 10 % de celle française réside à moins de 30km du littoral).[2] Pour quantifier et prévoir les impacts de ces phénomènes, il est possible de modéliser différents types de houle.
Ainsi notre étude porte sur les houles et leur impact sur le littoral. Afin de les étudier nous partirons du modèle de Berkhoff et nous utiliserons la méthode par homotopie pour résoudre les équations des différents cas que nous étudierons. Nous les comparerons ensuite aux solutions analytiques de façon graphique pour attester de l'efficacité de la méthode.
Lien de la vidéo illustratrice de notre sujet :
https://youtu.be/H_ZsmYrNXQM
[modifier] Modèle de Berkhoff
Ce modèle a pour expression (en bi-dimensionnel):
$ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $
où $ \phi $ est le potentiel, k est le nombre d’onde fonction de la profondeur H et de la fréquence $ \omega $ (T est la période), par la relation implicite $ \omega^2=gk \tanh(kH) $ , C est la célérité de l’onde, Cg est la célérité de groupe des vagues.
Pour simplifier le problème, nous nous placerons dans le domaine des ondes longues, ce qui signifie que $ C=C_g=\sqrt{gH} $.
L'évolution dans le temps de la hauteur de houle est donnée par : $ h(x,t)=\Re \left (\phi e^{-i\omega t} \right ) $.
[modifier] Cas n°1 :
Canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $ (condition de Dirichlet) et sortie libre amont $ \phi_x=ik\phi $ (condition de Robin).
[modifier] Solution analytique
On part de l'équation initiale :
$ \operatorname{grad}(C\cdot C_g\cdot \operatorname{grad}(\phi)) + k^2\cdot C\cdot C_g\cdot \phi = 0 $
En appliquant la formule du Laplacien, on obtient : $ C\cdot C_g\cdot \operatorname{grad}(\operatorname{grad}(\phi)) + k^2\cdot C\cdot C_g\cdot \phi = 0 $ Ce qui se simplifie en : $ C\cdot C_g\cdot \nabla^2\phi + k^2\cdot C\cdot C_g\cdot \phi = 0 $
En factorisant, on a : $ (C\cdot C_g\cdot \nabla^2 + k^2\cdot C\cdot C_g)\cdot \phi = 0 $
On peut réécrire l'opérateur différentiel sous la forme : $ C\cdot C_g\cdot \nabla^2 + k^2\cdot C\cdot C_g = C\cdot C_g\cdot \frac{\partial^2}{\partial x^2} + k^2\cdot C\cdot C_g $
Ainsi, l'équation devient : $ (C\cdot C_g\cdot \frac{\partial^2}{\partial x^2} + k^2\cdot C\cdot C_g)\cdot \phi = 0 $
Et en réarrangeant les termes, on obtient : $ \frac{\partial^2 \phi}{\partial x^2} + k^2\cdot \phi = 0 $
Ainsi, la solution est de la forme : $ \phi(x) = A \cdot e^{ikx} + B \cdot e^{-ikx} $ où A et B sont des constantes à déterminer.
On a $ \phi(0) = A + B = 1 $, donc $ B = 1 - A $.
En utilisant $ \frac{d\phi}{dx}\biggr\rvert_{x=L} = i k \phi(L) $, on a :
$ ik(Ae^{ikL} - Be^{-ikL}) = ik\phi(L) $
Or $ ik\phi(L)=ik(Ae^{ikL} + Be^{-ikL}) $
Pour avoir $ ik(Ae^{ikL} - Be^{-ikL}) = ik(Ae^{ikL} + Be^{-ikL}) $ et sachant que $ B = 1 - A $, il faut nécessairement : $ A=1 $ et $ B=0 $
Ainsi on a $ \phi(x) = e^{ikx} = \cos(kx) + i\sin(kx) $
[modifier] Solution par homotopie
[modifier] Ordre 0
$ \phi_{0,xx}=0 $ soit $ \phi_0=Ax+B $.
En introduisant les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, il vient :
$ \phi_0=1+\dfrac{ik}{1-ikL}x $.
[modifier] Ordre 1
$ \phi_{1,xx}-\phi_{0,xx}+\phi_{0,xx}+k^2\phi_0=0 $ soit $ \phi_{1}=-k^2\int\phi_0dxdx +Ax+B $.
En introduisant les conditions limites suivantes: $ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $, il vient : $ \phi_1=- \dfrac{k^2L(k^2L^2+3ikL-3} {3(1-ikL)^2}x-k^2\left (\dfrac{ik} {6(1-ikL)}x^3+\dfrac{1} {2}x^2 \right ) $
[modifier] Ordre 2
En réutilisant la décomposition par série entière, on arrive pour l'ordre 2 à :
$ \phi_{2,xx} = -k^2 \phi_{1} $. ce qui nous amène à :
$ \phi_{2}=-k^2 \iint \phi_{1} \mathrm{d}x + Ax + B $.
On a comme conditions initiales : $ \phi_{2}^0=0 $ qui donne $ B = 0 $. et $ \phi_{2,x}^L = ik\phi_{2}^L $. qui donne $ A\left(1-ikL\right) = k^2 \int \phi_{1} \mathrm{d}x - ik^3 \iint \phi_{1} \mathrm{d}x \mathrm{d}x + ik $. on résout alors pour arriver à $ A = x^2 \left[\frac{-k^4L\left(k^2L^2 + 3ikL -3\right)}{6\left(1-ikL\right)^3}\right] + x^3 \left[\frac{-3k^2\left(1-ikL\right)^3 + ik^5L \left(k^2L^2+3ikL-3\right)}{18\left(1-ikl\right)^3} \right] + x^4 \left[\frac{k^2\left(1-ikL\right)^3 - ik^3}{24\left(1-ikL\right)^2}\right]-\frac{x^5k^3i}{120\left(1-ikL\right)^2} + \frac{ik}{1-ikL} $.
On remplace alors les constantes par leurs expressions et on a :
$ \phi_{2} = k^2\left[ \frac{-k^2L \left(k^2L^2+3ikL-3\right)x^3}{18\left(1-ikL\right)^2} - k^2\left(\frac{ikx^5}{120\left(1-ikL\right)} + \frac{x^4}{24} \right) \right] + x^3 \left[\frac{-k^4L\left(k^2L^2 + 3ikL -3\right)}{6\left(1-ikL\right)^3}\right] + x^4 \left[\frac{-3k^2\left(1-ikL\right)^3 + ik^5L \left(k^2L^2+3ikL-3\right)}{18\left(1-ikl\right)^3} \right] + x^5 \left[\frac{k^2\left(1-ikL\right)^3 - ik^3}{24\left(1-ikL\right)^2}\right]-\frac{x^5k^3i}{120\left(1-ikL\right)^2} + \frac{ik}{1-ikL} + 1 $.
[modifier] Cas n°2 :
Domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ \phi_x=ik(2-\phi) $ et réflexion totale amont $ \phi_x=0 $
[modifier] Solution analytique :
On reprend la même forme d'équation que pour le cas 1 et on cherche de nouvelles constantes A et B avec les nouvelles conditions initiales.
Pour l'équation $ \phi(x) = A \cdot e^{ikx} + B \cdot e^{-ikx} $, avec les conditions initiales $ \phi'(0) = i k (2-\phi(0)) $ et $ \phi'(L) = 0 $, on a :
En dérivant $ \phi(x) $, on trouve $ \phi'(x) = ik\cdot A \cdot e^{ikx} + ik\cdot B \cdot e^{-ikx} $.
En utilisant la condition $ \phi'(0) = i k (2-\phi(0)) $, on obtient $ \phi'(0) = ikA - ikB = ik (A-B) = ik (2-\phi(0)) $, donc on a $ A-B =(2-\phi(0))=(2-A-B) $, ce qui équivaut à $ A=1 $.
En utilisant la condition $ \phi'(L) = 0 $, on a $ \phi'(L) = A\cdot e^{ikL} - B\cdot e^{-ikL} = e^{ikL} - B\cdot e^{-ikL} = 0 $.
Cela équivaut à $ B\cdot e^{-ikL} = e^{ikL} $. D'où $ B= e^{2ikL} $.
Ainsi, $ \phi(x) = e^{ikx}(1 + e^{2ik(L-x)}) $
[modifier] Solution par homotopie :
[modifier] Ordre 0 :
Le développement de l'expression donne à l'ordre 0 :
$ \phi_{0,xx}=0 \Rightarrow \phi_{0}(x)=Ax+B $
La première condition initiale donne : $ \phi_{0,x}^L=0 \Rightarrow \phi_{0}(x)=B $
Le deuxième donne $ \phi_{0,x}^0=ik(2-\phi_{0}^0) \Rightarrow B=2 $
Ainsi $ \phi_{0}(x)=2 $
[modifier] Ordre 1 :
$ \phi_1(x)=-k^2\int\phi_0(x)dxdx+Ax+B $ d'où: $ \phi_{1,x}(x)=-k^2\int\phi_0(x)dx+A $
Condition limite en x=0 :
- $ \phi_{1,x}(x=0)=-ik \phi_{1}(x=0) $ soit $ \left|-k^2\int\phi_0(x)dx+A\right|_{x=0}=ik\left|-k^2\int\phi_0(x)dxdx+Ax+B\right|_{x=0}==>A=-ikB $
Condition limite en x=L :
- $ \phi_{1,x}(x=L)=0 $ soit $ \left|-k^2\int\phi_0(x)dx+A\right|_{x=L}=0 ==>A=k^2\int\phi_0(x)dx==>A=2k^2L $
on en déduit: $ \phi_1(x)=-k^2x^2+2k^2Lx+2ikL $
[modifier] Ordre 2 :
On a $ \phi_2 = k^2 \iint\phi_1 \mathrm{d}x + Ax + B $.
Et la condition initiale en 0 donne $ A = -ikB $
La seconde condition initiale nous donne $ A = k^2 \int\phi_1 \mathrm{d}x $.
Le calcul de A donne : $ A = \frac{2}{3}k^4L^3 + 2ik^3L^2 $ et alors $ B = -\frac{2}{3} ik^3L^3 + 2ik^2L^2 $.
En remplaçant les constantes dans l'expression de $ \phi_2 $ on obtient : $ \phi_2 = \frac {k^4x^4}{12} - \frac{k^4Lx^3}{3} - ik^3L^2 + x\frac{2}{3}k^4L^3 + 2ik^3L^2x -\frac{2}{3} ik^3L^3 + 2ik^2L^2 $
[modifier] Cas n°3 :
Domaine monodimensionnel de longueur L avec pente du fond constante (s=cste) avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $ et sortie libre amont $ \phi_x=ik\phi $
[modifier] Solution analytique
Reprenons l'équation de Berkhoff : $ \operatorname{grad}(C\cdot C_g\cdot \operatorname{grad}(\phi)) + k^2\cdot C\cdot C_g\cdot \phi = 0 $ . On considère à présent $ C $ et $ C_g $ non constantes. On a donc $ \operatorname{grad}(g\cdot H\cdot \operatorname{grad}(\phi)) + k^2\cdot g\cdot H\cdot \phi = 0 $. Cela donne $ g\cdot H\cdot \frac{\partial^2 \phi}{\partial x^2} -s\cdot g\cdot \frac{\partial \phi}{\partial x} + k^2\cdot g\cdot H\cdot \phi = 0 $. Puis on divise par g.
Si k est non constant ($ k= k_0\cdot \sqrt{\frac{H_0}{H(x)}} $), on obtient $ H(x)\cdot \frac{\partial^2 \phi}{\partial x^2} -s\cdot \frac{\partial \phi}{\partial x} + k_0^2\cdot H_0\cdot \phi = 0 $. On effectue le changement de variable suivant : $ H(x)=z=H_0-sx $. On obtient alors : $ zs^2 \frac{\partial^2 \phi}{\partial z^2} +s^2 \frac{\partial \phi}{\partial z} + k_0^2\cdot H_0\cdot \phi = 0 $.
En prenant $ \alpha^2 = (\frac{k_0}{s})^2 H_0 $, On obtient une équation de Bessel : $ z \frac{\partial^2 \phi}{\partial z^2} + \frac{\partial \phi}{\partial z} + \alpha^2\cdot \phi = 0 $.
La solution de cette équation de Bessel est de la forme : $ \phi(z)=AJ_0(2\alpha\sqrt{z}) + BY_0(2\alpha\sqrt{z}) $ avec :
$ J_0 $ la fonction de Bessel de première espèce
$ Y_0 $ la fonction de Bessel de deuxième espèce
A et B sont des constantes.
Or on a pour les conditions aux limites :
$ \phi(0) = 1 $
$ \phi_x(L)=ik\phi(L) $
Ainsi : $ AJ_0(2\alpha\sqrt{H_0}) + BY_0(2\alpha\sqrt{H_0})=1 $
Et : $ \frac{\alpha S}{\sqrt{H_0-sL}}(AJ_1(2\alpha\sqrt{H_0-sL}) + BY_1(2\alpha\sqrt{H_0-sL})) = ik(AJ_0(2\alpha\sqrt{H_0-sL}) + BY_0(2\alpha\sqrt{H_0-sL})) $
On pose alors : $ Y_0^0 = Y_0(2\alpha\sqrt{H_0}) $
$ J_0^0 = J_0(2\alpha\sqrt{H_0}) $
$ J_0^L = J_0(2\alpha\sqrt{H_0-sL}) $
$ Y_0^L = Y_0(2\alpha\sqrt{H_0-sL}) $
$ J_1^L = J_1(2\alpha\sqrt{H_0-sL}) $
$ Y_1^L = Y_1(2\alpha\sqrt{H_0-sL}) $
De plus, on remarque que $ \frac{\alpha S}{\sqrt{H_0-sL}} = k $.
On a alors : $ A=\frac{1-BY_1(2\alpha \sqrt{H_0})}{J_0(2\alpha \sqrt{H_0})} $ En remplaçant A dans la deuxième équation, on obtient alors $ B = \frac{iJ_0^L - J_1^L}{J_0^0(Y_1^L-iY_0^L) + Y_0^0(iJ_0^L - J_1^L)} $
On obtient $ A=\frac{1}{J_0^0} - \frac{(iJ_0^L - J_1^L)Y_1^0}{J_0^0(J_0^0(Y_1^L - iY_0^L) + Y_0^0(iJ_0^L - J_1^L))} $
Ainsi, $ \phi(z)= (\frac{1}{J_0^0} - \frac{(iJ_0^L - J_1^L)Y_1^0}{J_0^0(J_0^0(Y_1^L - iY_0^L) + Y_0^0(iJ_0^L - J_1^L))}) J_0(2\alpha\sqrt{z}) + \frac{iJ_0^L - J_1^L} {J_0^0(Y_1^L-iY_0^L) + Y_0^0(iJ_0^L - J_1^L)}Y_0(2\alpha\sqrt{z}) $
[modifier] Solution par homotopie
Pour ce cas les conditions aux limites sont : $ \phi(0)= 1 $ et $ \phi_x^L=ik\phi^L $
Cas où k est constant
On a les mêmes conditions aux limites que le cas n°1 où on a aussi $ k=k_0 $ constant donc on retrouve les mêmes résultats que pour le cas n°1
Cas où k est variable
On a $ k=k_0\sqrt{\frac{H_0}{H(x)}} $
[modifier] Ordre 0 :
On a $ \phi_{0,xx} = 0 \Rightarrow \phi_0(x)=Ax+B $
Avec les conditions aux limites on détermine $ B=1 $ et $ A(1-ik_LL) = ik_L $
On résout pour trouver A : $ A=\frac{ik_L}{1-ik_LL} $ avec $ k_L=k_0\sqrt{\frac{H_0}{H_L}} $
Ce qui donne comme résultat final : $ \phi_0(x)=\frac{ik_L}{1-ik_LL}x+1 $
[modifier] Ordre 1 :
L'équation à résoudre est : $ (H_0-sx)\phi_{xx}-s\phi_x+k_0^2H_0\phi=0 $
On pose $ \epsilon = \frac{s}{H_0} $
La relation d'homotopie donne ainsi : $ \phi_{1,xx}=\epsilon\phi_{0,x}-k_0^2\phi_0 $
On intègre pour arriver à $ \phi_1(x)=\epsilon\frac{ik_L}{1-ik_LL}\frac{x^2}{2}-k_0^2[\frac{x^2}{2}+\frac{ik_L}{1-ik_LL}\frac{x^3}{6}]+A_1x+B_1 $
Avec les conditions initiales on détermine A et B :
$ \phi_1(0)=0 \Rightarrow B_1=0 $
et $ \phi_{1,x}^L=ik_L\phi_1^L \Rightarrow A_1= \frac{ik_L}{1-ik_LL}[\epsilon\frac{ik_L}{1-ik_LL}\frac{L^2}{2}-k_0^2(\frac{L^2}{2}+\frac{ik_L}{1-ik_LL}\frac{L^3}{6})]-\epsilon\frac{ik_L}{(1-ik_LL)^2}L+k_0^2[L+\frac{ik_L}{1-ik_LL}\frac{L^2}{2}] $
[modifier] Cas n°4
Vague sphérique générée par une source périodique sinusoïdale.
Nous traitons ici de l'évolution de la surface libre dans un domaine infini en grande profondeur. La source ponctuelle est appliquée autour d'un cercle de rayon r_0 centré sur un domaine circulaire de rayon R qui laisse sortir librement cette onde en r=R. l'équation de Berkhoff se simplifie alors en équation de Helmholtz et s'exprime en coordonnées polaires avec les conditions suivantes:
$ \phi_{rr}+\frac{1}{r}\phi_r+k^2\phi=0 $, $ \phi^0=1 $,$ \phi^R=ik\phi_r $
[modifier] Solution analytique
Dans le cas de l'équation de Helmholtz en coordonnées polaires pour un cercle, la forme de la solution utilisant les fonctions de Bessel est donnée par :
$ \phi(r) = [A J₀(kr) + B Y₀(kr)] $
On a les conditions initiales suivantes :
$ \phi(r_0) = 1 $
$ \phi_r (R) = ik\phi(R) $
Sachant que $ J_0'=-J_1 $ et $ Y_0'=-Y_1 $ , on obtient les deux équations suivantes :
$ AJ_0(r_0) + BY_0(r_0) = 1 $
$ -AJ_1(R) - BY_1(R) = ik(AJ_0(R) + BY_0(R)) $
Ainsi, on obtient :
$ A = \frac{Y_1(R)+ikY_0(R)}{-Y_0(r_0)J_1(R)+J_0(r_0)Y_1(R)-ikJ_0(R)Y_0(r_0)+ikJ_0(r_0)Y_0(R)} $
Et : $ B = \frac{1}{Y_0(r_0)} - \frac{J_0(r_0)(Y_1(R)+ikY_0(R))}{Y_0(r_0)(Y_1(R)J_0(r0)+ikY_0(R)J_0(r0)−J_1(R)Y_0(r0)−ikJ_0(R)Y_1(R))} $
Ainsi :
$ \phi(r) = [ \frac{Y_1(R)+ikY_0(R)}{-Y_0(r_0)J_1(R)+J_0(r_0)Y_1(R)-ikJ_0(R)Y_0(r_0)+ikJ_0(r_0)Y_0(R)}J₀(kr) +(\frac{1}{Y_0(r_0)} - \frac{J_0(r_0)(Y_1(R)+ikY_0(R))}{Y_0(r_0)(Y_1(R)J_0(r0)+ikY_0(R)J_0(r0)−J_1(R)Y_0(r0)−ikJ_0(R)Y_1(R))})Y₀(kr)] $
[modifier] Solution par homotopie
[modifier] Ordre 0 :
On a $ \phi_{0,rr}=0 \Rightarrow \phi_0(r)=Ar+B $
On utilise les conditions initiales pour déterminer A et B :
$ \phi_0^{r_0}=1 \Rightarrow Ar_0+B=1 $
$ \phi_r^{r=R}=ik\phi^{r=R} \Rightarrow A(1-ikR)=ikB $
On forme ainsi un système de deux équations et deux inconnues qui donne une fois résout :
$ A=\frac{ik}{ik(r_0-R)+1} $ et $ B=1-\frac{r_0ik}{ik(r_0-R)+1} $
Ce qui donne $ \phi_0(r)=r\frac{ik}{ik(r_0-R)+1}+1-\frac{r_0ik}{ik(r_0-R)+1} $
[modifier] Ordre 1 :
On a $ \phi_{1r,r}(r)+\frac{1}{r}\phi_{0,r}(r)+k^2\phi_0(r)=0 $
On remplace $ \phi_0 $ et $ \phi_{0,r} $ par leur expression avec $ A_0 = \frac{ik}{ik(r_0-R)+1} $ et $ B_0=1-\frac{r_0ik}{ik(r_0R)+1} $
$ \Rightarrow \phi_{1,rr}=-\frac{1}{R_0}A_0-k^2(A_0r+B_0) $
On intègre deux fois $ \phi_1(r)=-(rln(r)-r)A_0-k^2(A_0\frac{r^3}{6}+B_0{r^2}{2})+A_1r+B_1 $
On détermine $ A_1 $ et $ B_1 $ avec les conditions initiales :
$ \phi_1^{r_0}=0 \Rightarrow B_1=0 $
$ \phi_{1,r}^R=ik\phi_1^R \Rightarrow A_1=\frac{1}{1-ik}[[(Rln(R)-R)A_0+k^2(A_0A_0\frac{R^3}{6}+B_0\frac{R^2}{2})]ik-ln(R)A_0-k^2(A_0\frac{R^2}{2}+B_0R)] $
[modifier] Bibliographie
[1] Milieu Marin France. « Érosion côtière ». https://www.milieumarinfrance.fr/Nos-rubriques/Etat-du-milieu/Erosion-cotiere.
[2] UP’ Magazine. « Sur les plages de l’Atlantique, l’érosion côtière révèle les lacunes juridiques françaises » https://up-magazine.info/planete/climat/85226-sur-les-plages-de-latlantique-lerosion-cotiere-revele-les-lacunes-juridiques-francaises/.
[3] Vercelot, Salomé. « Ce sont les communes les plus touchées par l’érosion du littoral en France ». Futura. https://www.futura-sciences.com/planete/actualites/environnement-ce-sont-communes-plus-touchees-erosion-littoral-france-98355/.
 S'abonner à un flux RSS
S'abonner à un flux RSS