Perte de charge linéaire (HU) : Différence entre versions
m (1 version) |
|||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Friction loss'' | ''<u>Traduction anglaise</u> : Friction loss'' | ||
| − | [[Perte de charge (HU)|Perte de charge]] due aux | + | [[Perte de charge (HU)|Perte de charge]] due aux frottements sur les parois et à la viscosité du fluide dans les parties courante du réseau. |
| − | frottements sur les parois et à la viscosité du fluide dans les parties | + | |
| − | courante du réseau. | + | |
== Formule universelle des pertes de charge == | == Formule universelle des pertes de charge == | ||
| − | Les pertes de charge linéaires sont généralement représentées | + | Les pertes de charge linéaires sont généralement représentées par la pente de la ligne de charge (pertes de charge par unité de longueur). Il est important de noter que l'on intègre généralement dans les pertes de charge linéaires les pertes de charges dues aux « macro-aspérités » du réseau (branchements, câbles, échelles, etc.). La formule universelle des pertes de charge s'exprime sous la forme : |
| − | par la pente de la ligne de charge (pertes de charge par unité de longueur). Il | + | |
| − | est important de noter que l'on intègre généralement dans les pertes de charge | + | |
| − | linéaires les pertes de charges dues aux « macro-aspérités » du | + | |
| − | réseau (branchements, câbles, échelles, etc.). La formule universelle des | + | |
| − | pertes de charge s'exprime sous la forme : | + | |
| − | <center> | + | <center><math>Δh=\frac{λ.V^2.L}{2.g.D_h}\quad ou \quad J=\frac{λ.V^2}{2.g.D_h}\quad(1)</math></center> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
Avec : | Avec : | ||
| − | + | * <math>λ</math> : coefficient de pertes de charge (sans dimension) ; | |
| − | + | * <math>D_h</math> : diamètre hydraulique de la conduite (<math>D_h = 4.R_h</math>) (<math>m</math>) ; | |
| − | + | * <math>g</math> : accélération de la pesanteur (<math>m/s²</math>) ; | |
| − | hydraulique de la conduite ( | + | * <math>h</math> : pertes de charge pour un tronçon de longueur <math>L</math> (<math>m</math>) ; |
| − | + | * <math>J</math> : pertes de charge par unité de longueur (<math>m/m</math>) ; | |
| − | + | * <math>L</math> : longueur du tronçon (<math>m</math>) ; | |
| − | de la pesanteur (m/s²) ; | + | * <math>V</math> : vitesse moyenne de l'écoulement (<math>m/s</math>). |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | de charge par unité de longueur (m/m) ; | + | |
| − | + | ||
| − | + | ||
| − | du tronçon (m) ; | + | |
| − | + | ||
| − | + | ||
| − | moyenne de l'écoulement (m/s). | + | |
== Estimation du coefficient de pertes de charge == | == Estimation du coefficient de pertes de charge == | ||
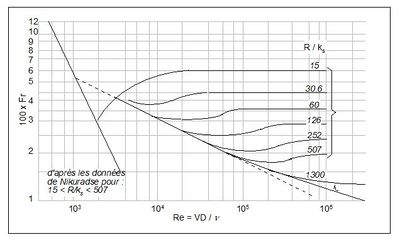
| − | Le coefficient de pertes de charge | + | Le coefficient de pertes de charge est fonction de la [[Rugosité (HU)|rugosité]] des parois, de la [[Viscosité (HU)|viscosité]] du fluide et du diamètre hydraulique de la conduite. Il existe de nombreuses formules pour le calculer. Voir [[Bazin Henry (1829-1917) (HU)|Bazin]], [[Colebrook Cyril Frank (1910-1997) (HU)|Colebrook]], [[Manning-Strickler (formule de) (HU)|Manning-Strickler]]. |
| − | est fonction de la [[Rugosité (HU)|rugosité]] des parois, de la [[Viscosité (HU)|viscosité]] du fluide et du | + | |
| − | diamètre hydraulique de la conduite. Il existe de nombreuses formules pour le | + | |
| − | calculer. Voir [[Bazin Henry (1829-1917) (HU)|Bazin]], [[Colebrook Cyril Frank (1910-1997) (HU)|Colebrook]], [[Manning-Strickler (formule de) (HU)|Manning-Strickler]]. | + | |
| + | [[File:harpe_nikuradze.JPG|400px|center|thumb|<center>''La harpe de Nikuradse ; d'après [Graf, 1993]''.</center>]] | ||
| + | En régime [[Ecoulement uniforme (HU)|uniforme]], à surface libre, la dépense d'énergie due aux pertes de charge linéaires équilibre exactement l'énergie fournie par les forces de pesanteur. On a donc <math>I = J</math>, si <math>I</math> représente la pente du tronçon, soit : | ||
| − | <center> | + | <center><math>I=\frac{λ.V^2}{2.g.D_h}\quad soit encore \quad V=\sqrt{2.g.(4.R_h).\frac{L}{λ}.I}\quad(2)</math></center> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
soit enfin : | soit enfin : | ||
| + | <center><math>V=C.\sqrt{R_h).I}\quad avec \quad C = sqrt{\frac{8.g}{λ}}\quad(3)\quad</math>(formule de Chézy)</center> | ||
| − | < | + | <u>Voir aussi</u> : [[Coefficient de rugosité (HU)|Coefficient de rugosité]]. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | de rugosité]]. | + | |
| − | [[Catégorie: | + | [[Catégorie:Dictionnaire_DEHUA]] |
Version du 14 janvier 2020 à 13:47
Traduction anglaise : Friction loss
Perte de charge due aux frottements sur les parois et à la viscosité du fluide dans les parties courante du réseau.
Formule universelle des pertes de charge
Les pertes de charge linéaires sont généralement représentées par la pente de la ligne de charge (pertes de charge par unité de longueur). Il est important de noter que l'on intègre généralement dans les pertes de charge linéaires les pertes de charges dues aux « macro-aspérités » du réseau (branchements, câbles, échelles, etc.). La formule universelle des pertes de charge s'exprime sous la forme :
Avec :
- $ λ $ : coefficient de pertes de charge (sans dimension) ;
- $ D_h $ : diamètre hydraulique de la conduite ($ D_h = 4.R_h $) ($ m $) ;
- $ g $ : accélération de la pesanteur ($ m/s² $) ;
- $ h $ : pertes de charge pour un tronçon de longueur $ L $ ($ m $) ;
- $ J $ : pertes de charge par unité de longueur ($ m/m $) ;
- $ L $ : longueur du tronçon ($ m $) ;
- $ V $ : vitesse moyenne de l'écoulement ($ m/s $).
Estimation du coefficient de pertes de charge
Le coefficient de pertes de charge est fonction de la rugosité des parois, de la viscosité du fluide et du diamètre hydraulique de la conduite. Il existe de nombreuses formules pour le calculer. Voir Bazin, Colebrook, Manning-Strickler.
En régime uniforme, à surface libre, la dépense d'énergie due aux pertes de charge linéaires équilibre exactement l'énergie fournie par les forces de pesanteur. On a donc $ I = J $, si $ I $ représente la pente du tronçon, soit :
soit enfin :
Voir aussi : Coefficient de rugosité.
 S'abonner à un flux RSS
S'abonner à un flux RSS