Manning-Strickler (formule de) (HU) : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Manning-Stricker's formula'' | ''<u>Traduction anglaise</u> : Manning-Stricker's formula'' | ||
| − | + | <u>Dernière mise à jour</u> : 23/1/2020 | |
| − | + | ||
| − | + | ||
| − | + | Formule permettant d'évaluer le paramètre C de l'équation de [[Chézy (formule de) (HU)|Chézy]] et de calculer les [[Perte de charge linéaire (HU)|pertes de charge linéaires]] par unité de longueur. | |
| − | + | ||
| + | == Formulation == | ||
| + | La formule de Manning-Strickler peut se mettre sous la forme : | ||
| − | |||
| − | + | <center><math>C = K.R_h^{1/6}\quad(1)</math></center> | |
| − | + | En intégrant cette formulation dans la formule de Chézy, on obtient : | |
| − | |||
| − | + | <center><math>V=C.\sqrt{R_h.J} = K.R_h^{1/6}.\sqrt{R_h.J}= K.R_h^{2/3}.J^{1/2}\quad(2)</math></center> | |
| − | |||
| − | |||
| − | + | Avec : | |
| − | + | ||
| − | + | ||
| − | + | * <math>C</math> : coefficient de Chezy (m<sup>1/2</sup>/s) ; | |
| − | + | * <math>J</math> : pertes de charge (<math>m/m</math>) (égale à la pente du [[Radier (HU)|radier]] dans le cas d'un [[Ecoulement uniforme (HU)|régime uniforme]]) ; | |
| − | des parois (m | + | * <math>K</math> : coefficient fonction de la [[Rugosité (HU)|rugosité]] des parois (m^{1/3}/s) ; |
| + | * <math>R_h</math> : [[Rayon hydraulique (HU)|rayon hydraulique]] (<math>m</math>) ; | ||
| + | * <math>V</math> : vitesse moyenne de l'écoulement (<math>m/</math>s). | ||
| − | + | == Estimation du coefficient K == | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
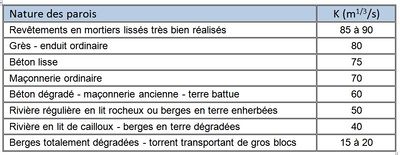
| + | La formule de Chézy tient compte à la fois des pertes de charges dues à la [[Viscosité (HU)|viscosité]] du fluide et de celles dues à la [[Rugosité (HU)|rugosité]] des parois. Le choix de la valeur numérique attribuée au coefficient de Manning-Strickler devrait donc également tenir compte de ces deux éléments. En pratique, on fait le plus souvent l'hypothèse que la viscosité de l'eau est suffisamment constante pour que l'on puisse relier la valeur du coefficient de pertes de charges à la nature des parois. Le tableau de la figure donne un exemple de table d'affectation. | ||
| + | [[File:manning.JPG|400px|center|thumb|<center>''Exemples de valeurs du coefficient de Manning-Strickler pour différents matériaux.''</center>]] | ||
| − | + | Il est important de préciser que la rugosité des parois doit tenir compte, non seulement de la dimension des aspérités, mais également des macro-obstacles à l'écoulement que l'on peut rencontrer dans les systèmes d’assainissement (coudes, chutes, câbles accrochés aux parois, etc.). Ce n'est pas le cas des valeurs fournies par les fabricants de conduites qui correspondent à des mesures de laboratoire et qui peuvent de ce fait être beaucoup plus fortes que celles de la conduite en service dans des conditions réelles. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ( | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <u>Voir aussi</u> : [[Coefficient de rugosité (HU)|Coefficient de rugosité]]. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
Version du 23 janvier 2020 à 22:34
Traduction anglaise : Manning-Stricker's formula
Dernière mise à jour : 23/1/2020
Formule permettant d'évaluer le paramètre C de l'équation de Chézy et de calculer les pertes de charge linéaires par unité de longueur.
Formulation
La formule de Manning-Strickler peut se mettre sous la forme :
En intégrant cette formulation dans la formule de Chézy, on obtient :
Avec :
- $ C $ : coefficient de Chezy (m1/2/s) ;
- $ J $ : pertes de charge ($ m/m $) (égale à la pente du radier dans le cas d'un régime uniforme) ;
- $ K $ : coefficient fonction de la rugosité des parois (m^{1/3}/s) ;
- $ R_h $ : rayon hydraulique ($ m $) ;
- $ V $ : vitesse moyenne de l'écoulement ($ m/ $s).
Estimation du coefficient K
La formule de Chézy tient compte à la fois des pertes de charges dues à la viscosité du fluide et de celles dues à la rugosité des parois. Le choix de la valeur numérique attribuée au coefficient de Manning-Strickler devrait donc également tenir compte de ces deux éléments. En pratique, on fait le plus souvent l'hypothèse que la viscosité de l'eau est suffisamment constante pour que l'on puisse relier la valeur du coefficient de pertes de charges à la nature des parois. Le tableau de la figure donne un exemple de table d'affectation.
Il est important de préciser que la rugosité des parois doit tenir compte, non seulement de la dimension des aspérités, mais également des macro-obstacles à l'écoulement que l'on peut rencontrer dans les systèmes d’assainissement (coudes, chutes, câbles accrochés aux parois, etc.). Ce n'est pas le cas des valeurs fournies par les fabricants de conduites qui correspondent à des mesures de laboratoire et qui peuvent de ce fait être beaucoup plus fortes que celles de la conduite en service dans des conditions réelles.
Voir aussi : Coefficient de rugosité.
 S'abonner à un flux RSS
S'abonner à un flux RSS