Contrainte de cisaillement (HU) : Différence entre versions
(→Contrainte de cisaillement en mécanique des fluides) |
|||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Shear stress'' | ''<u>Traduction anglaise</u> : Shear stress'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 07/09/2021 |
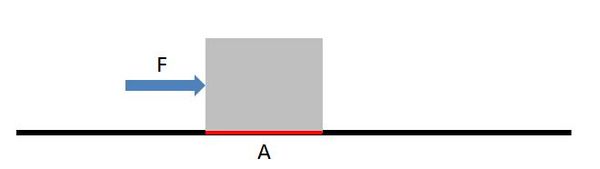
Contrainte mécanique appliquée de manière tangentielle à une face d'un matériau ; comme toute contrainte, elle s'exprime sous la forme du rapport d'une force à une surface (voir figure 1). | Contrainte mécanique appliquée de manière tangentielle à une face d'un matériau ; comme toute contrainte, elle s'exprime sous la forme du rapport d'une force à une surface (voir figure 1). | ||
| Ligne 14 : | Ligne 14 : | ||
| − | [[File:cisaillement.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : La contrainte | + | [[File:cisaillement.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : La contrainte de cisaillement appliquée sur la surface <math>A</math>, parallèle à la force <math>F</math> est égale à <math>τ</math>.''</center>]] |
==Contrainte de cisaillement en mécanique des fluides== | ==Contrainte de cisaillement en mécanique des fluides== | ||
Version du 7 septembre 2021 à 13:36
Traduction anglaise : Shear stress
Dernière mise à jour : 07/09/2021
Contrainte mécanique appliquée de manière tangentielle à une face d'un matériau ; comme toute contrainte, elle s'exprime sous la forme du rapport d'une force à une surface (voir figure 1).
Avec :
- $ τ $ : contrainte de cisaillement (Pa) ;
- $ F $ : Force tangentielle à la face (N) ;
- $ A $ : Surface de la face (m^2) ;
Contrainte de cisaillement en mécanique des fluides
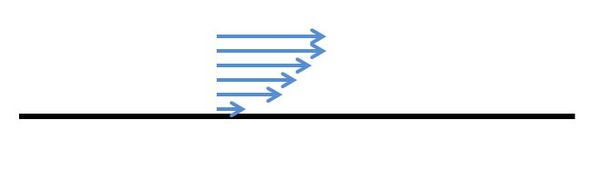
Une contrainte de cisaillement se développe sur chaque particule fluide chaque fois que l'on met un fluide en mouvement sur une surface fixe. Celle-ci est simplement due au gradient de vitesse qui s'établit à l'intérieur du fluide à partir du fond (ou des parois) (voir figure 2). Ces contraintes de cisaillement provoquent une déformation angulaire du fluide, dont l'importance dépend de sa viscosité.
Une contrainte de cisaillement s'applique également pour toute particule ou objet présent dans l'écoulement et conditionne donc le transport solide. Si l'objet est posé sur le fond il sera mis en mouvement dès que cette contrainte deviendra supérieure à une contrainte critique (voir Diagramme de Shields (HU)), ce qui se produira dès que la vitesse de l'écoulement près du fond deviendra supérieure à la vitesse de cisaillement.
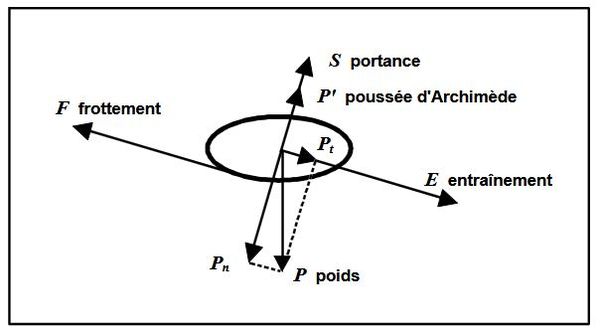
Ces grandeurs limites peuvent être déterminées en écrivant le bilan des forces qui s'appliquent sur une particule solide posée au fond (voir figure 3).
 S'abonner à un flux RSS
S'abonner à un flux RSS