Isochrones (méthode des courbes) (HU) : Différence entre versions

Version du 19 septembre 2019 à 11:33

Traduction anglaise : Isochron map method

Méthode permettant de calculer l'hydrogramme à l'exutoire d'un bassin versant, correspondant à une pluie quelconque connue par son hyétogramme. Elle porte également le nom de méthode rationnelle généralisée.

Principes et formulation

Une courbe isochrone est définie comme l'ensemble des points d'un bassin versant tels que le temps mis par l'eau pour parcourir le trajet entre le point considéré et l'exutoire soit égal à une valeur donnée. On suppose en général que ce temps est constant, c'est à dire indépendant du débit instantané et de son évolution précédente. Si ces hypothèses sont vérifiées, tout bassin versant peut être décomposé en sous bassins, limités par des courbes isochrones.

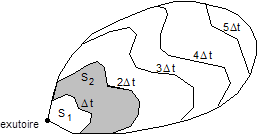
Figure 1 : Sur cet exemple, le bassin versant a été décomposé en 6 sous bassins, limités par des courbes isochrones séparées par des durées fixes et égales à Dt.

Utilisation pratique

A partir des courbes isochrones, il est possible de construire un graphe aire/temps, permettant de calculer l'évolution de la surface théorique contribuant au ruissellement en fonction du temps écoulé depuis le début de la pluie.

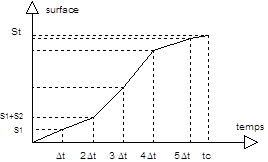
Figure 2 : Exemple de diagramme aire-temps permettant de calculer la surface contribuant à l'écoulement à l'exutoire en fonction du temps écoulé depuis le début de la pluie.

On obtient ainsi un moyen simple de calculer l'hydrogramme à l'exutoire du bassin versant, par une simple sommation des débits générés par chacun des sous bassins. Par exemple :

· si le bassin versant est découpé en k éléments de surface Aj, de coefficient de ruissellement Cj, avec i variant de 1 à k, et de temps de parcours Dt ;

· si la pluie est discrétisée en m pas de temps Dt ;

alors l'hydrogramme résultant au nième pas de temps Dt répond à :

Avec :

·

pour j > k ;

· Ij : intensité de la pluie au jème pas de temps (

pour j > m).

Lien avec les modèles à réservoir

La méthode des courbes isochrones constitue une fonction de transfert particulière, fondée sur la seule prise en compte de la translation du débit dans le système (l'évolution des volumes stockés n'est pas considérée en tant que tel). Si l'on fait tendre vers zéro le temps séparant deux lignes isochrones successives, le débit à l'exutoire ne s'exprime alors plus par la somme d'un nombre fini de termes, mais par l'intégrale du produit de l'intensité instantanée par une fonction représentative de la courbe aire-temps. En terme mathématiques, il s'agit d'un produit de convolution, et la fonction représentative de la courbe aire-temps constitue l'intégrale de l'Hydrogramme unitaire instantané (HUI), caractéristique de la réponse du bassin versant.

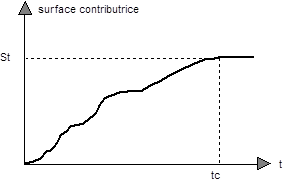
Figure 3 : Courbe aire-temps.

La méthode des courbes isochrones peut donc, dans sa formulation finale être rapprochée de la méthode de l'hydrogramme unitaire. Si la répartition des surfaces suit une loi exponentielle décroissante, l'hydrogramme unitaire instantané devient alors celui du réservoir linéaire.

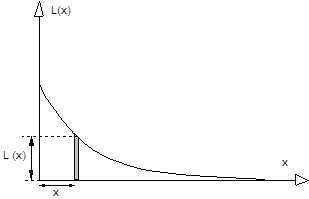
Figure 4 : Représentation de la fonction L(x).

Les hypothèses nécessaires sont les suivantes :

· L(x) représente la largeur du bassin versant à la distance x de l'exutoire ;

· la vitesse d'écoulement sur le bassin versant est constante, le temps nécessaire pour que l'eau aille de la bande de terrain D(x).dx, jusqu'à l'exutoire est proportionnel à x.

Dans ces conditions la surface drainante à l'instant t (diagramme aire-temps) est :

Deux approches radicalement différentes : le modèle conceptuel du réservoir linéaire ne tenant compte que du stockage, et le modèle empirique des courbes isochrones, ne tenant compte que de la translation fournissent exactement la même équation pratique.

Limites d'utilisation

Les principales difficultés d'utilisation de cette méthode sont les suivantes :

· l'hypothèse de la constance des vitesses d'écoulement est rarement vérifiée ;

· le découpage aire/temps est généralement difficile ;

· l'estimation des coefficients de ruissellement Cj est également délicate.