Premier flot (effet de) (HU) : Différence entre versions

Version du 22 janvier 2020 à 16:48

Traduction anglaise : Fisrt flush, First foul flush

Dernière mise à jour : 22/1/2020

Concept selon lequel les effluents transitant dans un système d’assainissement pluvial, ou dans un système d’assainissement unitaire, seraient beaucoup plus pollués au début de l'événement pluvieux que dans la suite de son déroulement.

Cette hypothèse, si elle était valide, serait extrêmement séduisante car elle justifierait que l'on ne traite que la partie la plus polluée des effluents, c'est à dire celle qui se présente au début de la pluie. Malheureusement les choses ne sont pas aussi simples.

Concepts de base

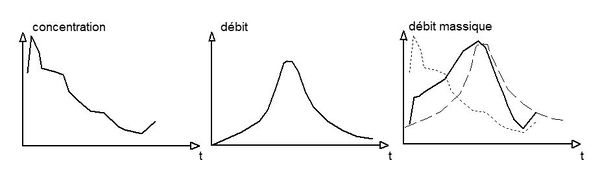
La répartition des masses rejetées en fonction du temps au cours d'un événement, constitue un élément important à connaître, en particulier pour choisir des stratégies de traitement. On peut représenter cette répartition par un pollutogramme représentant soit les variations de la concentration en fonction du temps, soit les variations du débit massique en fonction du temps. Ces deux représentations ne sont absolument pas identiques. En effet le débit massique est égal au produit de la concentration par le débit. Une concentration même très élevée au début de l'événement, lorsque le débit est très faible ne garantit absolument pas qu'une fraction importante de la masse transite au début de l'événement.

La figure 1 illustre les différentes courbes possibles (hydrogramme, pollutogramme en concentration et pollutogramme en débit massique).

Figure 1 : Un effet de premier flot sur un pollutogramme en concentration ne garantit pas que le même phénomène existe sur le pollutogramme en débit massique.

Mise en évidence du phénomène de premier flot

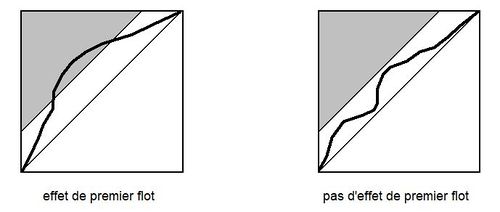
Pour étudier de façon plus objective la présence ou non d'un effet de premier flot exploitable, il est maintenant d'usage de représenter le pourcentage de la masse rejetée en fonction du pourcentage du volume écoulé au point de rejet ($ M = f (V) $). La figure 2 illustre une telle représentation :

Figure 2 : M et V sont exprimées de façon adimensionnelle en les divisant respectivement par la masse totale et le volume total écoulé.

• si la concentration en polluant est constante pendant l’événement, alors la courbe sera confondue avec la diagonale ;
• si la concentration est supérieure au début de la pluie, alors la courbe sera au dessus de la diagonale et il y aura donc un effet de premier flot.

Exploitabilité du phénomène de premier flot

La définition précédente est cependant insuffisante pour décider si l'effet de premier flot est effectivement exploitable. Pour ceci il est nécessaire de quantifier l'écart par rapport à la diagonale et également de préciser le moment où cet écart est important.

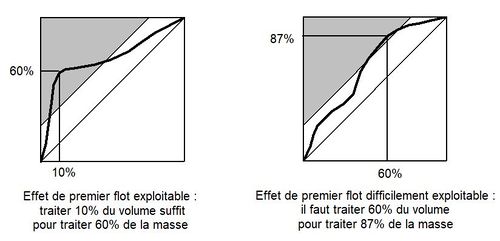
On considère souvent (Geiger, 1984) que l'effet de premier flot est exploitable dès lors que l'écart entre la courbe M = f (V) et la bissectrice est supérieur à 20%, c'est à dire si, pour une valeur particulière de V, f (V) > V + 0,2 (voir figure 3).

Figure 3 : Définition quantitative de l'effet de premier flot, d'après Geiger (1984).

Cette approche est cependant insuffisante car elle ne tient pas compte du moment où l'écart dépasse effectivement les 20%. Si l'écart entre les deux courbes est maximum à la fin de l'événement son exploitation est en effet difficile car elle impose de traiter malgré tout un volume d'eau très important (voir figure 4).

Figure 4 : Nécessité de prendre en compte le temps pour évaluer l'intérêt d'exploiter l'effet de premier flot.

Pour éliminer cet inconvénient, Bertrand-Krajewski et al. (1995) ont proposé la démarche suivante :

• on approxime la courbe $ M = f (V) $ par une fonction de la forme $ M = V^b $ (ce type d'ajustement est généralement satisfaisant, au vu des incertitudes sur les mesures disponibles sur $ M $ et $ V $ ;
• on mesure l'écart entre la courbe $ M = f (V) = V^b $ et la diagonale ($ M = V $), par la valeur du paramètre $ b $.

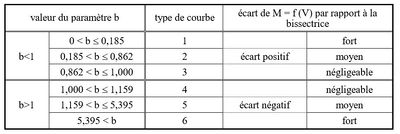
Les auteurs proposent de classer les courbes en six catégories, selon la valeur de b. Le tableau de la figure 5 présente cette classification.

Figure 5 : Caractéristiques des courbes $ M = f (V) $ en fonction du paramètre $ b $.

Le premier flot est alors défini par l’une des trois propositions équivalentes suivantes :

• la valeur de $ b $ est inférieure à 0,185 ;
• la courbe $ M = f (V) $ appartient à la catégorie 1 ;
• plus de 80% de la charge polluante est transportée dans les 30 premiers % du volume.

Ce critère peut paraître sévère ; il correspond cependant à un seuil raisonnable si l'on désire obtenir des rendements épuratoires voisins de ceux des stations d'épuration en ne traitant qu'une faible partie des effluents. Un rendement de 80% obtenu sur 80% de la masse n'élimine en effet que 64% de la charge polluante.