Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/DAVID-POULTIER-TORNES : Différence entre versions
(→Discriminant négatif : p^2) |
(→Discriminant négatif : p^2) |
||
| Ligne 71 : | Ligne 71 : | ||
==== Discriminant négatif : <math> p^2 < 4k^2 </math> ==== | ==== Discriminant négatif : <math> p^2 < 4k^2 </math> ==== | ||
Dans le cas où <math>p^{2}<4k^{2}</math>, on a <math>\Delta =p^{2}-4k^{2}<0\\</math> | Dans le cas où <math>p^{2}<4k^{2}</math>, on a <math>\Delta =p^{2}-4k^{2}<0\\</math> | ||
| − | |||
La solution de <math>x^{2}-px+k^{2}</math> s'écrit donc : | La solution de <math>x^{2}-px+k^{2}</math> s'écrit donc : | ||
| − | |||
<math>x= \frac{-b\pm i\sqrt{\vert b^{2}-4ac\vert }}{2a}=\frac{p\pm | <math>x= \frac{-b\pm i\sqrt{\vert b^{2}-4ac\vert }}{2a}=\frac{p\pm | ||
i\sqrt{\vert p^{2}-4k^{2}\vert }}{2}=\frac{p}{2} \pm i\frac{\sqrt{\vert | i\sqrt{\vert p^{2}-4k^{2}\vert }}{2}=\frac{p}{2} \pm i\frac{\sqrt{\vert | ||
p^{2}-4k^{2}\vert }}{2} \\</math> | p^{2}-4k^{2}\vert }}{2} \\</math> | ||
| − | |||
On pose alors :<math>r=\frac{p}{2}</math> et <math>\omega =\frac{\sqrt{\vert | On pose alors :<math>r=\frac{p}{2}</math> et <math>\omega =\frac{\sqrt{\vert | ||
p^{2}-4k^{2}\vert }}{2}\\</math> | p^{2}-4k^{2}\vert }}{2}\\</math> | ||
| − | |||
On en déduit la solution générale de l'équation différentielle est : | On en déduit la solution générale de l'équation différentielle est : | ||
| − | |||
<math>\Phi (x)= e^{rx}(C_{1}\cos (\omega x)+C_{2}\sin (\omega x))\\</math> | <math>\Phi (x)= e^{rx}(C_{1}\cos (\omega x)+C_{2}\sin (\omega x))\\</math> | ||
| − | |||
On a alors les conditions initiales suivantes : <math>\lbrace \begin{matrix} | On a alors les conditions initiales suivantes : <math>\lbrace \begin{matrix} | ||
| Ligne 96 : | Ligne 90 : | ||
\end{matrix} | \end{matrix} | ||
\rbrace \\</math> | \rbrace \\</math> | ||
| − | |||
en 0 :<math> \Phi (0)=C_{1}=1\\</math> | en 0 :<math> \Phi (0)=C_{1}=1\\</math> | ||
| − | |||
en L : <math>\Phi _{x}(L)=re^{rL}(C_{2}\omega \cos (\omega L)-\omega \sin | en L : <math>\Phi _{x}(L)=re^{rL}(C_{2}\omega \cos (\omega L)-\omega \sin | ||
(\omega L))\\ | (\omega L))\\ | ||
| − | |||
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =ike^{rL}(\cos (\omega | \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =ike^{rL}(\cos (\omega | ||
L)+C_{2}\sin (\omega L)) | L)+C_{2}\sin (\omega L)) | ||
| − | |||
\leftrightarrow C_{2}=\frac{r\omega \sin (\omega L)+ikcos(\omega | \leftrightarrow C_{2}=\frac{r\omega \sin (\omega L)+ikcos(\omega | ||
L)}{r\omega \cos (\omega L)-iksin(\omega L)}\\</math> | L)}{r\omega \cos (\omega L)-iksin(\omega L)}\\</math> | ||
| − | |||
et donc on a :<math> \Phi (x)= e^{rx}(\cos (\omega x)+ \frac{r\omega \sin | et donc on a :<math> \Phi (x)= e^{rx}(\cos (\omega x)+ \frac{r\omega \sin | ||
(\omega L)+ikcos(\omega L)}{r\omega \cos (\omega L)-iksin(\omega L)}\sin | (\omega L)+ikcos(\omega L)}{r\omega \cos (\omega L)-iksin(\omega L)}\sin | ||
(\omega x))\\ | (\omega x))\\ | ||
| − | |||
\Phi (x)=e^{rx}(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega | \Phi (x)=e^{rx}(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega | ||
| Ligne 121 : | Ligne 109 : | ||
}{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x)) | }{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x)) | ||
\\</math> | \\</math> | ||
| − | |||
| − | |||
| − | |||
avec :<math> r=\frac{p}{2} et \omega =\frac{\sqrt{\vert p^{2}-4k^{2}\vert | avec :<math> r=\frac{p}{2} et \omega =\frac{\sqrt{\vert p^{2}-4k^{2}\vert | ||
}}{2}\\</math> | }}{2}\\</math> | ||
| − | |||
On en déduit :<math> \\ | On en déduit :<math> \\ | ||
| − | |||
Re(\Phi (x))=e^{rx}(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin | Re(\Phi (x))=e^{rx}(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin | ||
(\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)}{(r\omega | (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)}{(r\omega | ||
\cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))\\</math> | \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))\\</math> | ||
| − | |||
et <math> Im(\Phi (x))=e^{rx}( \frac{kr\omega }{(r\omega \cos (\omega | et <math> Im(\Phi (x))=e^{rx}( \frac{kr\omega }{(r\omega \cos (\omega | ||
L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))\\</math> | L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))\\</math> | ||
| − | |||
On a alors :<math> H(x)= \frac{Re(\Phi (x))}{|\Phi (x)|}\\ | On a alors :<math> H(x)= \frac{Re(\Phi (x))}{|\Phi (x)|}\\ | ||
| − | |||
= \frac{(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos | = \frac{(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos | ||
Version du 8 juin 2020 à 17:22
Sommaire |
Cas n°1
On s'intéresse à une onde se propageant dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une sortie libre en amont.
Équation de Berkhoff
On se place dans un domaine monodimensionnel de profondeur constante. L'équation se simplifie alors en $ \frac{\partial^2 \phi}{\partial x^2}+k^2\phi=0 $
Cette équation correspond à l'équation de Helmholtz.
Solution analytique
La forme des solutions est donc de la forme $ \phi(x)=A\mathrm{e}^{-\mathrm{i}kx}+B\mathrm{e}^{\mathrm{i}kx} $ où A et B sont deux constantes à déterminer grâce aux conditions aux limites $ \phi=1 $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=\mathrm{i}k\phi $ en $ x=L $.
On trouve alors $ A=0 $ et $ B=1 $ d'où $ \phi(x)=\mathrm{e}^{\mathrm{i}kx} $.
On peut alors trouver le potentiel temporel et en déduire la hauteur de la houle.
On a $ \phi(x)=\mathrm{e}^{\mathrm{i}(kx-\omega t)} $ d'où $ h(x,t)=\cos (kx-\omega t) $.
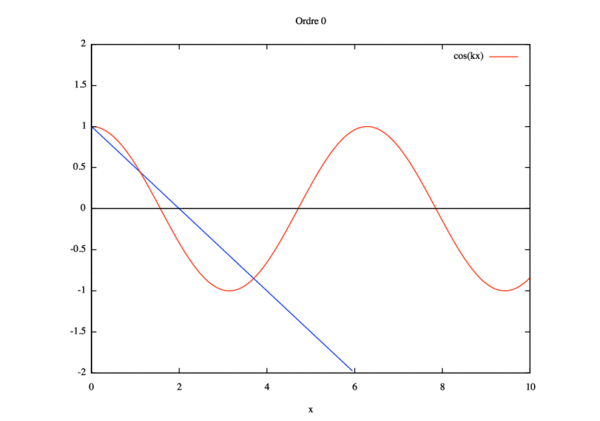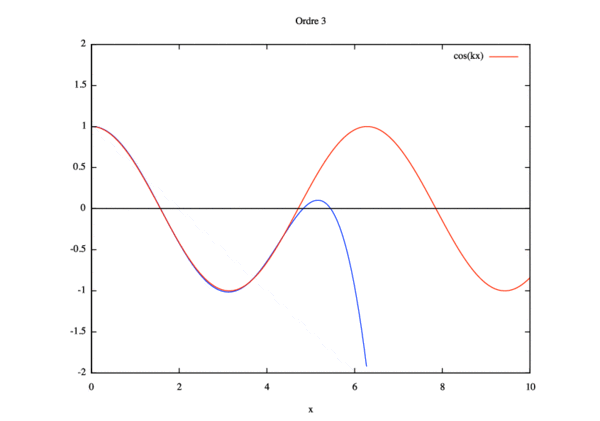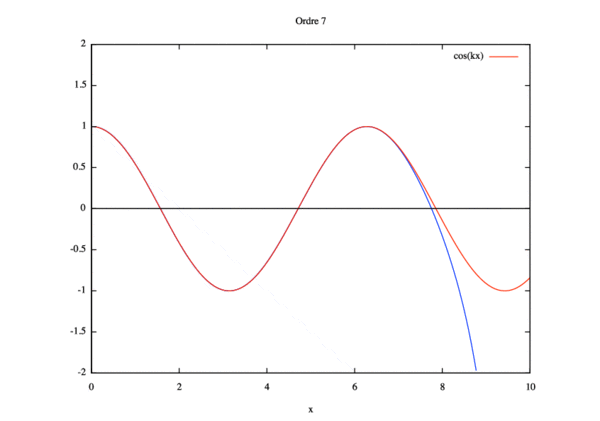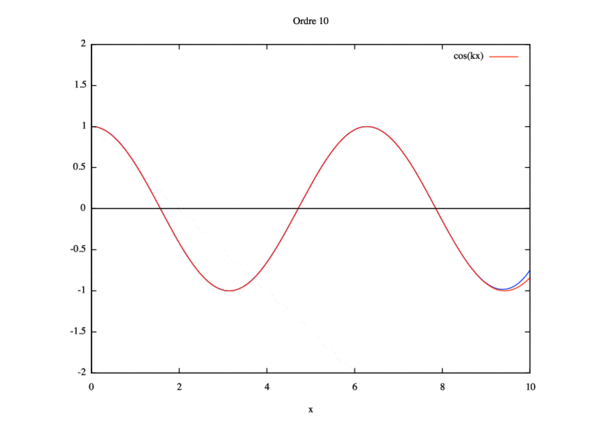
Résolution par homotopie
Cas n°2
On s'intéresse à une onde se propageant dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire ainsi qu'une condition de flux aval précisée plus loin et une réflexion totale en amont.
Équation de Berkhoff
L'équation reste la même que dans le cas n°1 :$ \frac{\partial^2 \phi}{\partial x^2}+k^2\phi=0 $.
Solution analytique
La forme des solutions est donc toujours de la forme $ \phi(x)=A\mathrm{e}^{-\mathrm{i}kx}+B\mathrm{e}^{\mathrm{i}kx} $ où A et B sont deux constantes à déterminer grâce aux conditions aux limites $ \frac{\partial \phi}{\partial x}=\mathrm{i}k(2-\phi) $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=0 $ en $ x=L $.
On trouve alors $ A=\mathrm{e}^{2\mathrm{i}kL} $ et $ B=1 $.
On en déduit alors $ \phi(x)=\mathrm{e}^{-\mathrm{i}(k(x-2L)+\omega t)}+\mathrm{e}^{\mathrm{i}(kx-\omega t)} $ et donc $ h(x,t)=\cos (k(x-L)) $.
Résolution par homotopie
Cas n°3
On s'intéresse à une onde se propageant dans un domaine monodimensionnel de longueur L avec pente du fond constante avec entrée par l'aval d'une onde fréquence unitaire et une sortie libre en amont. On supposera que le nombre d'onde $ k $ est constant.
Équation de Berkhoff
On se place dans un domaine monodimensionnel avec pente du fond constante. On va noter la pente $ H(x)=H_0-px $ où $ H_0 $ correspond à la hauteur initiale du fond et $ p $ correspond à la pente du fond.
L'équation s'écrit donc :
$ (H_0-px)\frac{\partial^2 \phi}{\partial x^2}-p\frac{\partial \phi}{\partial x}+k^2(H_0-px)\phi=0 $
On effectue alors le changement de variable $ X=\frac{k}{p}(H_0-px) $. L'équation devient alors :
$ pkX\frac{\partial^2 \phi}{\partial X^2}+pk\frac{\partial \phi}{\partial X}+pkX\phi=0 $
En divisant alors par $ pk $ et en multipliant par $ X $, on obtient alors l'équation de Bessel suivante :
$ X^2\frac{\partial^2 \phi}{\partial X^2}+X\frac{\partial \phi}{\partial X}+X^2\phi=0 $
Solution analytique
La forme des solutions est donc de la forme $ \phi(X)=AJ_0(X)+BY_0(X) $ où $ J_0 $ et $ Y_0 $ correspondent aux fonctions de Bessel respectivement de première et de deuxième espèce.
On effectue alors le changement de variable inverse :
$ \phi(x)=AJ_0(\frac{k}{p}(px-H_0))+BY_0(\frac{k}{p}(px-H_0)) $.
On pose $ x_L=\frac{k}{p}(pL-H_0) $ et $ x_0=-\frac{k}{p}H_0 $.
On trouve alors $ A=\frac{aY_1(x_L)+bY_0(x_L)+\mathrm{i}(aY_0(x_L)-bY_1(x_L))}{a^2+b^2} $ et $ B=\frac{aJ_1(x_L)+bJ_0(x_L)+\mathrm{i}(aJ_0(x_L)-bJ_1(x_L))}{a^2+b^2} $ en posant $ a=J_1(x_L)Y_0(x_0)-J_0(x_0)Y_1(x_L) $ et $ b=J_0(x_L)Y_0(x_0)-J_0(x_0)Y_0(x_L) $.
Finalement $ \phi(x)=(AJ_0(\frac{k}{p}(px-H_0))+BY_0(\frac{k}{p}(px-H_0)))\mathrm{e}^{-\mathrm{i}\omega t}. $
Alors $ H(x)=\frac{(\Re(A)J_0(\frac{k}{p}(px-H_0))+\Re(B)Y_0(\frac{k}{p}(px-H_0)))\cos(\omega t)+(\Im(A)J_0(\frac{k}{p}(px-H_0))+\Im(B)Y_0(\frac{k}{p}(px-H_0)))\sin(\omega t)}{\sqrt{(\Re(A)J_0(\frac{k}{p}(px-H_0))+\Re(B)Y_0(\frac{k}{p}(px-H_0)))^2+(\Im(A)J_0(\frac{k}{p}(px-H_0))+\Im(B)Y_0(\frac{k}{p}(px-H_0)))^2}} $
Résolution par homotopie
Cas n°1
On s'intéresse à une onde se propageant dans un domaine monodimensionnel de longueur L avec pente du fond exponentiel avec entrée par l'aval d'une onde fréquence unitaire et une sortie libre en amont.
Équation de Berkhoff
On se place dans un domaine monodimensionnel avec pente du fond exponentielle. On va noter la pente $ H(x)=H_0\mathrm{e}^{px} $ où $ H_0 $ correspond à la hauteur initiale du fond et $ p $ correspond à la pente du fond.
L'équation s'écrit donc :
$ \frac{\partial^2 \phi}{\partial x^2}-p\frac{\partial \phi}{\partial x}+k^2\phi=0 $
On en déduit alors l'équation caractéristque : $ r^2-pr+k^2 $ et ainsi le discrimant associé $ \Delta = p^2 -4k^2 $. Il faut donc résoudre suivant la valeur du discriminant.
Solution analytique
Discriminant positif : $ p^2 > 4k^2 $
Discriminant nul : $ p=2k $
Discriminant négatif : $ p^2 < 4k^2 $
Dans le cas où $ p^{2}<4k^{2} $, on a $ \Delta =p^{2}-4k^{2}<0\\ $
La solution de $ x^{2}-px+k^{2} $ s'écrit donc :
$ x= \frac{-b\pm i\sqrt{\vert b^{2}-4ac\vert }}{2a}=\frac{p\pm i\sqrt{\vert p^{2}-4k^{2}\vert }}{2}=\frac{p}{2} \pm i\frac{\sqrt{\vert p^{2}-4k^{2}\vert }}{2} \\ $
On pose alors :$ r=\frac{p}{2} $ et $ \omega =\frac{\sqrt{\vert p^{2}-4k^{2}\vert }}{2}\\ $
On en déduit la solution générale de l'équation différentielle est :
$ \Phi (x)= e^{rx}(C_{1}\cos (\omega x)+C_{2}\sin (\omega x))\\ $
On a alors les conditions initiales suivantes : $ \lbrace \begin{matrix} \Phi (0)=1 & \\ \Phi _{x}(L)=ik\Phi (L) & \\ \end{matrix} \rbrace \\ $
en 0 :$ \Phi (0)=C_{1}=1\\ $
en L : $ \Phi _{x}(L)=re^{rL}(C_{2}\omega \cos (\omega L)-\omega \sin (\omega L))\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =ike^{rL}(\cos (\omega L)+C_{2}\sin (\omega L)) \leftrightarrow C_{2}=\frac{r\omega \sin (\omega L)+ikcos(\omega L)}{r\omega \cos (\omega L)-iksin(\omega L)}\\ $
et donc on a :$ \Phi (x)= e^{rx}(\cos (\omega x)+ \frac{r\omega \sin (\omega L)+ikcos(\omega L)}{r\omega \cos (\omega L)-iksin(\omega L)}\sin (\omega x))\\ \Phi (x)=e^{rx}(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)+ikr\omega }{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x)) \\ $
avec :$ r=\frac{p}{2} et \omega =\frac{\sqrt{\vert p^{2}-4k^{2}\vert }}{2}\\ $
On en déduit :$ \\ Re(\Phi (x))=e^{rx}(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)}{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))\\ $
et $ Im(\Phi (x))=e^{rx}( \frac{kr\omega }{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))\\ $
On a alors :$ H(x)= \frac{Re(\Phi (x))}{|\Phi (x)|}\\ = \frac{(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)}{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))}{\sqrt{(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)}{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))^{2}+( \frac{kr\omega }{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))^{2}}}\\ $
 S'abonner à un flux RSS
S'abonner à un flux RSS