Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/DAVID-POULTIER-TORNES : Différence entre versions

Version du 11 juin 2020 à 11:39

Le thème de l'étude a pour but de modéliser l'impact du changement climatique sur les côtes en quantifiant l'impact des houles sur le littoral.
Afin de modéliser les houles, l'étude utilise le modèle de Berkhoff (ou équation de pente douce) qui intègre la repésentation des phénomènes de réfraction des fonds, le shoaling, la diffraction et la réflexion des structures côtières comme les digues ou les jétées.
Les équations obtenues seront résolues par uné méthode analytique ainsi qu'une méthode semi analytique : l'homotopie.

Equation de Berkhoff

Ce modèle a pour expression : $ \boxed{ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 } $

où $ \phi $ est le potentiel, k est le nombre d’onde fonction de la profondeur H et de la fréquence $ \omega $ (T est la période), par la relation implicite $ \omega^2=gk \tanh(kH) $ , C est la célérité de l’onde, Cg est la célérité de groupe des vagues.

Pour simplifier le problème, nous nous placerons dans le domaine des ondes longues, ce qui signifie que $ C=C_g=\sqrt{gH} $.

On peut alors déduire la hauteur de la houle : $ H_l(x)=\Re{(\phi)}/\left| \phi \right| $ et son évolution dans le temps: $ h(x,t)=\Re \left (H_l(x)e^{-i\omega t} \right ) $.

Canal uniforme plat avec sortie libre en amont

On s'intéresse à une onde se propageant dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une sortie libre en amont.

On se place dans un domaine monodimensionnel de profondeur constante. L'équation se simplifie alors en $ \frac{\partial^2 \phi}{\partial x^2}+k^2\phi=0 $
Cette équation correspond à l'équation de Helmholtz.

Solution analytique

La forme des solutions est donc de la forme $ \phi(x)=A\mathrm{e}^{-\mathrm{i}kx}+B\mathrm{e}^{\mathrm{i}kx} $ où A et B sont deux constantes à déterminer grâce aux conditions aux limites $ \phi=1 $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=\mathrm{i}k\phi $ en $ x=L $.
On trouve alors $ A=0 $ et $ B=1 $ d'où $ \phi(x)=\mathrm{e}^{\mathrm{i}kx} $.

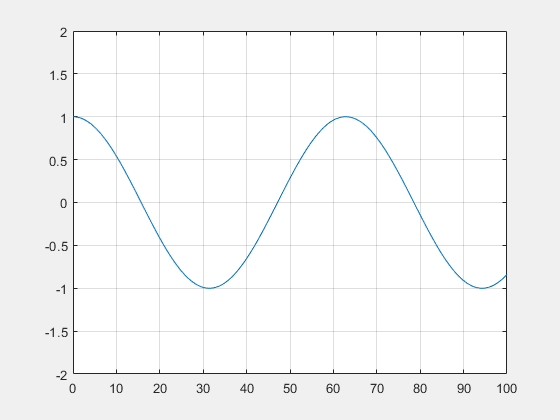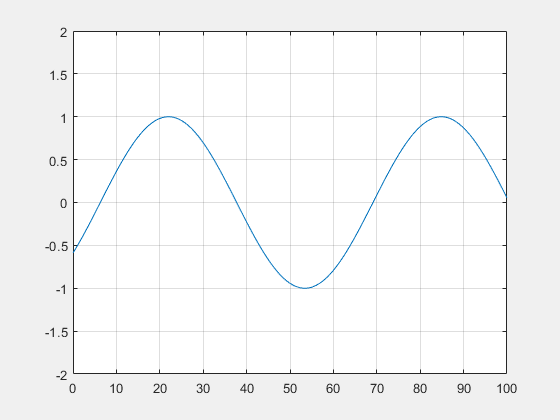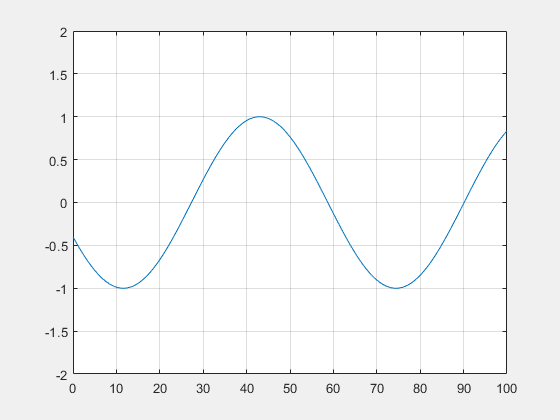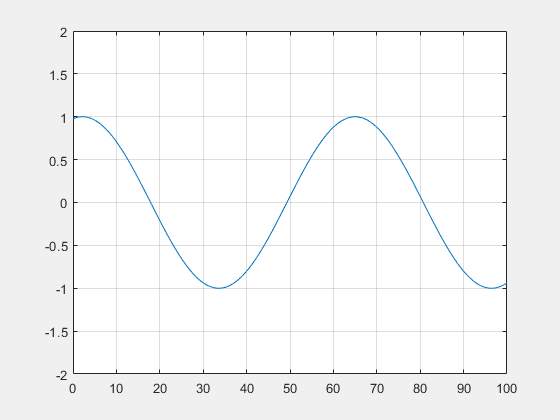
On peut alors déduire la hauteur de houle car $ \phi(x,t)=\mathrm{e}^{\mathrm{i}(kx-\omega t)} $ d'où $ \boxed{h(x,t)=\cos (kx-\omega t)} $.

Résolution par homotopie

La relation d'homotopie s'écrit $ (1-p)\Phi_{xx} +p(\Phi_{xx}+k^{2}\Phi)=0 $ qui se simplifie en $ \Phi_{xx} +pk^{2}\Phi=0 $. On prend $ u_{0}=0 $.

Ordre 0: L'équation s'écrit $ \Phi_{0,xx}=0 $.

Ainsi, on a $ \Phi_0=Ax+B $ où $ A $ et $ B $ sont deux constantes à déterminer avec les conditions aux limites énoncées précedemment.
On en déduit alors $ A=\frac{ik}{1-ikL} $ et $ B=1 $.

Finalement, on a $ \boxed{\Phi_0(x)=1+\dfrac{ik}{1-ikL}x} $.

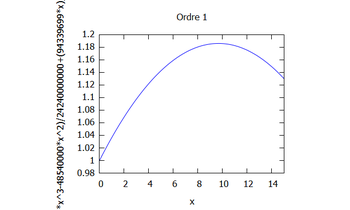
Ordre 1: L'équation s'écrit $ \Phi_{1,xx}+k^2\Phi_0=0 $.

Ainsi, on a $ \displaystyle\Phi_1+\iint\Phi_0+Ax+B=0 $. Pour déterminer les deux constantes, il faut choisir comme condition en amont $ \Phi_1(0)=0 $ puisque la condition $ \Phi_1(0)=1 $ a déjà été utilisé.
On en déduit alors $ A=\frac{3k^{2}L-2k^{4}L^{3}-3\mathrm{i}k^{3}L^{2}}{3(1-ikL)^{2}} $ et $ B=0 $.

Finalement, on a $ \boxed{\Phi_1(x)=-k^{2}\dfrac{ik}{1-ikL}\dfrac{x^{3}}{6}-k^{2}\dfrac{x^{2}}{2}+\frac{3k^{2}L-2k^{4}L^{3}-3\mathrm{i}k^{3}L^{2}}{3(1-ikL)^{2}}x} $.

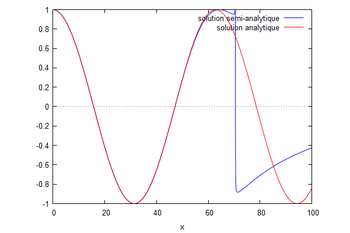
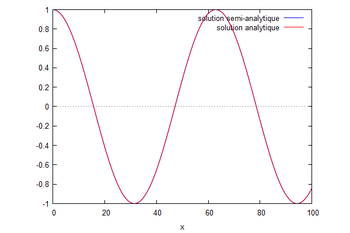
Ainsi, en déterminant tout les ordres jusqu'à un certain ordre $ n $ on obtient la solution $ \Phi(x)=\sum_{i=0}^{n}p^{i}\Phi_{i}(x) $. On peut alors évaluer ce polynôme en 1 et déterminer la hauteur de la houle.

Canal uniforme unidimensionnel plat avec réflexion totale en amont

On s'intéresse à une onde se propageant dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire ainsi qu'une condition de flux aval précisée plus loin et une réflexion totale en amont.

L'équation reste la même que dans le cas n°1 :$ \frac{\partial^2 \phi}{\partial x^2}+k^2\phi=0 $.

Solution analytique

La forme des solutions est donc toujours de la forme $ \phi(x)=A\mathrm{e}^{-\mathrm{i}kx}+B\mathrm{e}^{\mathrm{i}kx} $ où A et B sont deux constantes à déterminer grâce aux conditions aux limites $ \frac{\partial \phi}{\partial x}=\mathrm{i}k(2-\phi) $ en $ x=0 $ et $ \frac{\partial \phi}{\partial x}=0 $ en $ x=L $.
On trouve alors $ A=\mathrm{e}^{2\mathrm{i}kL} $ et $ B=1 $.

On en déduit alors $ \phi(x,t)=\mathrm{e}^{-\mathrm{i}(k(x-2L)+\omega t)}+\mathrm{e}^{\mathrm{i}(kx-\omega t)} $ et donc $ h(x,t)=\frac{\cos (kx-\omega t)+\cos(k(x-2L)+\omega t)}{\sqrt{2(1+\cos(2k(x-L))}} $ qui se simplifie en $ \boxed{h(x,t)=cos(kL-\omega t)} $.

Résolution par homotopie

La relation d'homotopie s'écrit toujours $ (1-p)\Phi_{xx} +p(\Phi_{xx}+k^{2}\Phi)=0 $ qui se simplifie en $ \Phi_{xx} +pk^{2}\Phi=0 $. On prend $ u_{0}=0 $.

Ordre 0: L'équation s'écrit $ \Phi_{0,xx}=0 $.

Ainsi, on a $ \Phi_0=Ax+B $ où $ A $ et $ B $ sont deux constantes à déterminer avec les conditions aux limites énoncées précedemment.
On en déduit alors $ A=0 $ et $ B=1 $.

Finalement, on a $ \boxed{\Phi_0(x)=2} $.

Ordre 1: L'équation s'écrit $ \Phi_{1,xx}+k^2\Phi_0=0 $.

Ainsi, on a $ \displaystyle\Phi_1+\iint\Phi_0+Ax+B=0 $. On en déduit alors $ A=2k^{2}L $ et $ B=2+2\mathrm{i}kL $.

Finalement, on a $ \boxed{\Phi_1(x)=-k^{2}x^{2}+2k^{2}Lx+2+2\mathrm{i}kL} $.

Canal uniforme unidimensionnel avec pente du fond constante

On s'intéresse à une onde se propageant dans un domaine monodimensionnel de longueur L avec pente du fond constante avec entrée par l'aval d'une onde fréquence unitaire et une sortie libre en amont. On supposera que le nombre d'onde $ k $ est constant.

On se place dans un domaine monodimensionnel avec pente du fond constante. On va noter la pente $ H(x)=H_0-px $ où $ H_0 $ correspond à la hauteur initiale du fond et $ p $ correspond à la pente du fond. L'équation s'écrit donc :
$ (H_0-px)\frac{\partial^2 \phi}{\partial x^2}-p\frac{\partial \phi}{\partial x}+k^2(H_0-px)\phi=0 $
On effectue alors le changement de variable $ X=\frac{k}{p}(H_0-px) $. L'équation devient alors :
$ pkX\frac{\partial^2 \phi}{\partial X^2}+pk\frac{\partial \phi}{\partial X}+pkX\phi=0 $
En divisant alors par $ pk $ et en multipliant par $ X $, on obtient alors l'équation de Bessel suivante :
$ X^2\frac{\partial^2 \phi}{\partial X^2}+X\frac{\partial \phi}{\partial X}+X^2\phi=0 $

Solution analytique

La forme des solutions est donc de la forme $ \phi(X)=AJ_0(X)+BY_0(X) $ où $ J_0 $ et $ Y_0 $ correspondent aux fonctions de Bessel respectivement de première et de deuxième espèce.
On effectue alors le changement de variable inverse :
$ \phi(x)=AJ_0(\frac{k}{p}(px-H_0))+BY_0(\frac{k}{p}(px-H_0)) $.
On pose $ x_L=\frac{k}{p}(pL-H_0) $ et $ x_0=-\frac{k}{p}H_0 $.
On trouve alors $ A=\frac{Y_1(x_L)-\mathrm{i}Y_0(x_L)}{\alpha} $ et $ B=\frac{J_1(x_L)+\mathrm{i}J_0(x_L)}{\alpha} $ en posant $ \alpha=(Y_1(x_L)-\mathrm{i}Y_0(x_L))J_0(x_0)+(J_1(x_L)+\mathrm{i}J_0(x_L))Y_0(x_0) $.
Finalement $ \boxed{\phi(x,t)=(AJ_0(\frac{k}{p}(px-H_0))+BY_0(\frac{k}{p}(px-H_0)))\mathrm{e}^{-\mathrm{i}\omega t}} $.

Résolution par homotopie

Cas n°4

On s'intéresse à une onde se propageant dans un domaine monodimensionnel de longueur L avec pente du fond exponentiel avec entrée par l'aval d'une onde fréquence unitaire et une sortie libre en amont.

Équation de Berkhoff

On se place dans un domaine monodimensionnel avec pente du fond exponentielle. On va noter la pente $ H(x)=H_0\mathrm{e}^{px} $ où $ H_0 $ correspond à la hauteur initiale du fond et $ p $ correspond à la pente du fond. L'équation s'écrit donc :
$ \frac{\partial^2 \phi}{\partial x^2}-p\frac{\partial \phi}{\partial x}+k^2\phi=0 $

On en déduit alors l'équation caractéristque : $ r^2-pr+k^2 $ et ainsi le discrimant associé $ \Delta = p^2 -4k^2 $. Il faut donc résoudre suivant la valeur du discriminant.

Solution analytique

Discriminant positif : $ p^2 > 4k^2 $

On a $ \Delta=p^2-4k^2>0 $. Alors on dispose de deux solutions réelles à savoir $ r_1 $ et $ r_2 $ telle que :

$ r_1 = \dfrac{p+\sqrt{p^2-4k^2}}{2}=\dfrac{p}{2}\left(1+\sqrt{1-4\left(\dfrac{k}{p}\right)^2}\right) $

$ r_2 = \dfrac{p}{2}\left(1-\sqrt{1-4\left(\dfrac{k}{p}\right)^2}\right) $

De plus on sait que l'ensemble des solutions de l'équation différentielle s'écrivent : $ Ae^{r_1x}+Be^{r_2x} $ avec $ (A,B)\in\mathbb{R}^2 $.

En utilisant les conditions aux limites $ \left\{\begin{matrix} \Phi(0)=1 \\ \left.\dfrac{\partial \Phi}{\partial x}\right|_{x=L}=ik\Phi(L) \end{matrix} \right. $ on obtient, $ \Phi(x=0)=A+B=1\Rightarrow \boxed{A+B=1} $

$ \left.\dfrac{\partial \Phi}{\partial x}\right|_{x=L} = r_1Ae^{r_1L}+r_2Be^{r_2L} $

$ ik\Phi(L) = ik\left(Ae^{r_1L}+Be^{r_2L}\right) $

D'où l'égalité $ r_1Ae^{r_1L}+r_2Be^{r_2L}=ik\left(Ae^{r_1L}+Be^{r_2L}\right) $ (i.e partie réelle = partie imaginaire)

Nécessairement : $ \left\{\begin{matrix} r_1Ae^{r_1L}+r_2Be^{r_2L} & = & 0 \quad (3) \\ Ae^{r_1L}+Be^{r_2L} &= & 0 \quad (2) \\ A+B & = & 1 \quad (1) \end{matrix}\right. $

Ainsi $ (1)\Longrightarrow Ae^{r_1L}+(1-A)e^{r_2L} = 0 $ donc $ A(e^{r_1L}-e^{r_2L})=-e^{r_2L} $

donc $ \boxed{A=\dfrac{-e^{r_2L}}{e^{r_1L}-e^{r_2L}}=\dfrac{1}{1-e^{(r_1-r_2)L}}} $ et $ \boxed{B=1-\dfrac{1}{1-e^{(r_1-r_2)L}}=-\dfrac{e^{(r_1-r_2)L}}{1-e^{(r_1-r_2)L}}} $

D'où le résultat final : $ \boxed{\Phi(x)=\dfrac{1}{1-e^{(r_1-r_2)L}}\left(e^{r_1x}-e^{(r_1-r_2)L}\times e^{r_2x}\right)} $

Discriminant nul : $ p=2k $

Discriminant négatif : $ p^2 < 4k^2 $

Dans le cas où $ p^{2}<4k^{2} $, on a $ \Delta =p^{2}-4k^{2}<0\\ $

La solution de $ x^{2}-px+k^{2} $ s'écrit :

$ x=\frac{p}{2} \pm i\frac{\sqrt{\vert p^{2}-4k^{2}\vert }}{2} \\ $

On pose :$ r=\frac{p}{2} $ et $ \omega =\frac{\sqrt{\vert p^{2}-4k^{2}\vert }}{2}\\ $

On en déduit la solution générale de l'équation différentielle :

$ \Phi (x)= e^{rx}(C_{1}\cos (\omega x)+C_{2}\sin (\omega x))\\ $

Avec les conditions initiales il vient :

en 0 :$ \Phi (0)=C_{1}=1\\ $

en L : $ \Phi _{x}(L)=re^{rL}(C_{2}\omega \cos (\omega L)-\omega \sin (\omega L))\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =ike^{rL}(\cos (\omega L)+C_{2}\sin (\omega L)) \leftrightarrow C_{2}=\frac{r\omega \sin (\omega L)+ikcos(\omega L)}{r\omega \cos (\omega L)-iksin(\omega L)}\\ $

et donc on a :$ \Phi (x)=e^{rx}(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)+ikr\omega }{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x)) \\ $

Et finalement:$ H(x)= \frac{Re(\Phi (x))}{|\Phi (x)|}\\ = \frac{(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)}{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))}{\sqrt{(\cos (\omega x)+ \frac{r^{2}\omega ^{2}\sin (\omega L)\cos (\omega L)-k^{2}\cos (\omega L)\sin (\omega L)}{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))^{2}+( \frac{kr\omega }{(r\omega \cos (\omega L))^{2}+(ksin(\omega L))^{2}}\sin (\omega x))^{2}}}\\ $

Résolution par homotopie

Equation différentielle: $ \frac{\partial ^{2}\Phi }{\partial x^{2}}-c\frac{\partial \Phi }{\partial x}+k^{2}\Phi =0\\ $

L'homotopie donne : $ (1-p)\lbrack \Phi _{xx}-u_{0,xx}\rbrack +p\lbrack \Phi _{xx}+p\Phi _{x}-k^{2}\Phi \rbrack =0\\ $

$ Ordre 0 :\Phi _{0,xx}-u_{0,xx}=0\\ $

$ Ordre 1 : \Phi _{1,xx}-k^{2}\Phi _{0}+c\Phi _{0,x}=0\\ $

$ Ordre 2 : \Phi _{2,xx}-k^{2}\Phi _{1}+c\Phi _{1,x}=0\\ $