Bernoulli (théorème de) (HU) : Différence entre versions
De Wikhydro
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Bernoulli's equation'' | ''<u>Traduction anglaise</u> : Bernoulli's equation'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 13/04/2021 |
| − | Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et permanent : | + | Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et [[Ecoulement permanent (HU)|permanent]] : |
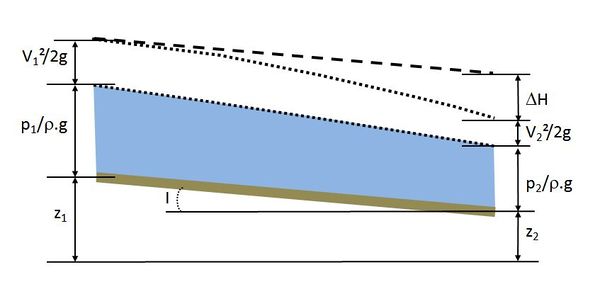
Il s'écrit en particulier, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2 - voir ''figure'' 1), sous la forme suivante : | Il s'écrit en particulier, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2 - voir ''figure'' 1), sous la forme suivante : | ||
| Ligne 19 : | Ligne 19 : | ||
* <math>g</math> : accélération de la pesanteur (<math>m/s^2</math>) ; | * <math>g</math> : accélération de la pesanteur (<math>m/s^2</math>) ; | ||
* <math>z</math> : altitude (<math>m</math>) ; | * <math>z</math> : altitude (<math>m</math>) ; | ||
| − | * <math>Δh</math> : pertes de charge dues aux frottements sur les parois et à la viscosité entre les sections 1 et 2 (<math>m</math>). | + | * <math>Δh</math> : pertes de charge dues aux frottements sur les parois et à la [[Viscosité (HU)|viscosité]] entre les sections 1 et 2 (<math>m</math>). |
Dans cette expression, l'énergie est exprimée en hauteur de fluide. Voir [[Charge hydraulique (HU)|Charge hydraulique]]. | Dans cette expression, l'énergie est exprimée en hauteur de fluide. Voir [[Charge hydraulique (HU)|Charge hydraulique]]. | ||
Version du 13 avril 2021 à 13:25
Traduction anglaise : Bernoulli's equation
Dernière mise à jour : 13/04/2021
Théorème traduisant la conservation de l'énergie mécanique dans un écoulement irrotationnel et permanent :
Il s'écrit en particulier, par unité de poids de liquide, entre deux sections quelconques d'un tube de courant (repérées par les indices 1 et 2 - voir figure 1), sous la forme suivante :
Avec :
- $ V $ : vitesse ($ m/s $) ;
- $ p $ : pression (pression atmosphérique si écoulement à surface libre) ($ P $a) ;
- $ h $ : hauteur d'eau ($ m $) ;
- $ ρ $ : masse volumique ($ kg/m^3 $) ;
- $ g $ : accélération de la pesanteur ($ m/s^2 $) ;
- $ z $ : altitude ($ m $) ;
- $ Δh $ : pertes de charge dues aux frottements sur les parois et à la viscosité entre les sections 1 et 2 ($ m $).
Dans cette expression, l'énergie est exprimée en hauteur de fluide. Voir Charge hydraulique.
 S'abonner à un flux RSS
S'abonner à un flux RSS