Ligne d'énergie (HU) : Différence entre versions
De Wikhydro
| Ligne 23 : | Ligne 23 : | ||
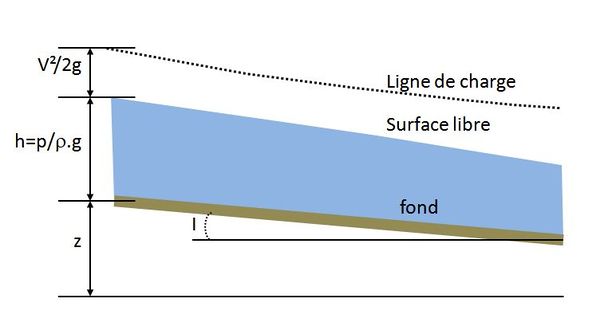
[[File:grandeurs_hydrauliques.JPG|600px|center|thumb|<center>''Figure 1'' : Différentes grandeurs hydrauliques.</center>]] | [[File:grandeurs_hydrauliques.JPG|600px|center|thumb|<center>''Figure 1'' : Différentes grandeurs hydrauliques.</center>]] | ||
| − | Cette quantité représente la charge totale par unité de | + | Cette quantité représente la charge totale par unité de volume de liquide (figure 1) et tient compte : |
* des termes de potentiel : altitude <math>z</math> ; | * des termes de potentiel : altitude <math>z</math> ; | ||
* des termes de pression : <math>\frac{p}{ρ.g}</math> égaux à la hauteur d'eau dans le cas d'une répartition hydrostatique et si on raisonne en pression relative, c'est à dire sans prendre en compte la pression atmosphérique ; | * des termes de pression : <math>\frac{p}{ρ.g}</math> égaux à la hauteur d'eau dans le cas d'une répartition hydrostatique et si on raisonne en pression relative, c'est à dire sans prendre en compte la pression atmosphérique ; | ||
Version du 26 mars 2022 à 16:11
Traduction anglaise : Head profile, Head line
Dernière mise à jour : 26/03/2022
Lieu des points représentant la charge hydraulique totale d'un l'écoulement ; on dit également ligne de charge.
Formulation mathématique
Dans le cas d'un écoulement à surface libre, cette ligne correspond aux variations, le long de l'écoulement, de la quantité :
Avec :
- $ z $ : altitude (m) ;
- $ p $ : pression (Pa ou N/m2) (nota : en général, on ne tient pas compte de la pression atmosphérique et on raisonne en pression relative en considérant une pression nulle en surface) ;
- $ ρ $ : masse volumique (kg/m3) ;
- $ g $ : accélération de la pesanteur (m/s2) ;
- $ V $ : vitesse moyenne de l'eau (m/s).
Cette quantité représente la charge totale par unité de volume de liquide (figure 1) et tient compte :
- des termes de potentiel : altitude $ z $ ;
- des termes de pression : $ \frac{p}{ρ.g} $ égaux à la hauteur d'eau dans le cas d'une répartition hydrostatique et si on raisonne en pression relative, c'est à dire sans prendre en compte la pression atmosphérique ;
- des termes d'énergie cinétique : $ \frac{V^2}{2.g} $.
 S'abonner à un flux RSS
S'abonner à un flux RSS