Contrainte de cisaillement (HU) : Différence entre versions

Version du 23 octobre 2023 à 14:14

Traduction anglaise : Shear stress

Dernière mise à jour : 23/10/2023

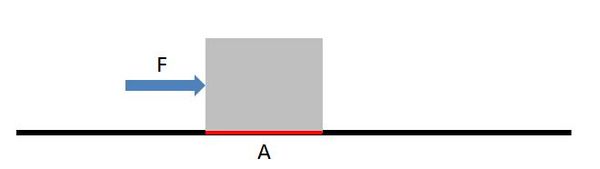
Contrainte mécanique appliquée de manière tangentielle à une face d'un matériau ; comme toute contrainte, elle s'exprime sous la forme du rapport d'une force à une surface (voir figure 1).

$ τ = \frac{F}{A} \qquad (1) $

Avec :

$ τ $ : contrainte de cisaillement (Pa) ;
$ F $ : Force tangentielle à la face (N) ;
$ A $ : Surface de la face (m²) ;

Figure 1 : La contrainte de cisaillement appliquée sur la surface $ A $, parallèle à la force $ F $ est égale à $ τ $.

Contrainte de cisaillement en mécanique des fluides

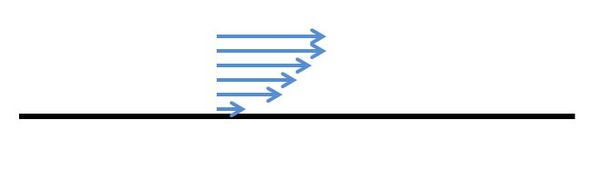
Une contrainte de cisaillement se développe sur chaque particule fluide chaque fois que l'on met un fluide en mouvement sur une surface fixe. Celle-ci est simplement due au gradient de vitesse qui s'établit à l'intérieur du fluide à partir du fond (ou des parois) (voir figure 2). Ces contraintes de cisaillement provoquent une déformation angulaire du fluide, dont l'importance dépend de sa viscosité (Oms, 2004).

Figure 2 : Le gradient de vitesse qui se développe à partir du fond (ou éventuellement des parois), supposé immobile, est à l'origine de contraintes de cisaillement qui s'appliquent sur toutes les particules fluides ainsi que sur les particules solides présentes dans l'écoulement ou sur le fond.

Von Karman a montré que dans un écoulement turbulent sur fond fixe rugueux de grande largeur (pour ne pas avoir à tenir compte des parois), la vitesse variait de façon logarithmique en fonction de la hauteur d'eau (relation (2)) :

$ \frac{u}{u_*} = \frac{1}{K}ln{\frac{h}{h_0}}+B_s\qquad(2) $

avec :

$ K $ : constante de Von Karman (sans dimension), dont la valeur est comprise entre 0,36 et 0,42 (normalement 0,41) ;
$ u $ : vitesse moyenne du fluide à la hauteur $ h $ (m/s) ;
$ h_0 $ : hauteur de rugosité (hauteur assimilée à celle pour laquelle $ u $ devient nulle) (m) ;
$ h $ : hauteur dans la veine liquide (m) ;
$ u_* $ : vitesse de frottement (m/s) ;
$ B_s $ : constante d'intégration fonction du nombre de Reynolds et dont la valeur est comprise entre 6 et 10 selon le type d'écoulement (sans dimension).

Contrainte de cisaillement sur les parois et lien avec les pertes de charge

Considérons un canal de forme quelconque et un écoulement uniforme à surface libre (figure 3).

Figure 3 : Les forces qui s'appliquent sur le volume de contrôle (en bleu) sont le poids, $ W $, les forces de frottement sur le fond et les parois, $ F $, et les forces de pression (qui s'annulent dans le cas d'un régime uniforme).

Dans le cas d'un régime uniforme, un volume de contrôle est simplement soumis à son poids et aux forces de frottement (il n'y a aucune accélération et les forces de pression s'annulent du fait de la répartition hydrostatique de cette dernière). La composante du poids parallèle à l'écoulement équilibre donc exactement les forces de frottement. On peut donc écrire la relation (3), en projetant ces forces sur un axe parallèle à l'écoulement :

$ F + W_x = 0 \qquad (3) $

La composante $ W_x $ du poids s’exprime par la relation (4) :

$ W_x = ρ.g.L.S.sin(α) \qquad (4) $

Avec :

$ ρ $ : masse volumique du fluide (kg/m³),
$ g $ : accélération gravitationnelle (m/s²),
$ S $ : section mouillée (m²),
$ L $ : longueur du volume de contrôle (m),
$ α $ : angle entre le fond du canal et l'horizontale.

La surface de frottement, $ A $, est égale au produit du périmètre mouillé, $ P $ (longueur du contact entre le fluide et les parois dans une section mouillée) par la longueur de frottement, $ L $, soit :

$ A = P.L \qquad (5) $

Comme l'angle $ α $ est petit, on peut assimiler $ sin(α) $ à la pente $ I $ du canal et obtenir la relation (6) qui permet le calcul de la contrainte de cisaillement sur les parois ou sur le fond, $ τ_w $ :

$ τ_w = \frac{F}{A} = \frac{ρ.g.L.S.sin(α)}{ P.L} = ρ.g.R_h.I\qquad (6) $

avec :

$ R_h $ : rayon hydraulique ($ R_h = \frac{S}{P} $) (m).

Cette relation peut être rapprochée de la formule permettant le calcul des pertes de charge, $ J $, dans le cas d'un régime uniforme (voir Coefficient de rugosité (HU)) :

$ J = \frac{λ.V^2}{8.ρ.g.R_h}\qquad (7) $

Avec :

$ λ $ : coefficient de pertes de charge (sans dimension) ;
$ R_h $ : rayon hydraulique de la conduite (m) ;
$ g $ : accélération de la pesanteur (m/s²) ;
$ J $ : pertes de charge par unité de longueur (m/m) ;
$ V $ : vitesse moyenne de l'écoulement (m/s).

Comme en régime uniforme $ I = J $, il existe donc une relation directe entre la vitesse moyenne de l'écoulement et la contrainte de cisaillement au voisinage des parois (relation (8)) :

$ V = \sqrt{\frac{8.τ_w}{λ}}\qquad (8) $

Utilisation en transport solide

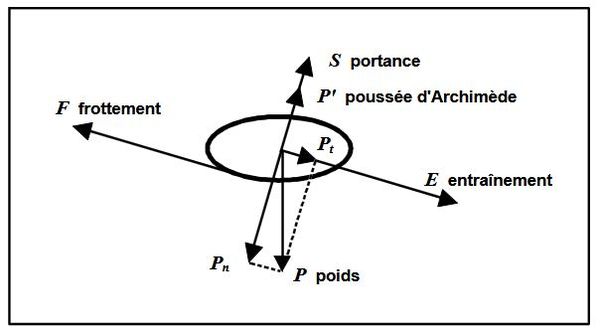
Une contrainte de cisaillement s'applique également pour toute particule ou objet présent dans l'écoulement et conditionne donc le transport solide. Si l'objet est posé sur le fond il sera mis en mouvement dès que cette contrainte, généralement notée $ τ_w $, deviendra supérieure à une contrainte critique, $ τ_* $, appelée contrainte critique d'entrainement ou seuil de cisaillement.

La contrainte de cisaillement près du fond, $ τ_w $, est reliée à la vitesse de frottement par la relation (3) :

$ τ_w = ρ.u_*^2\qquad(3) $

avec :

$ τ_w $ : contrainte de cisaillement près du fond (N/m²) ;
$ ρ $ : masse volumique du fluide (kg/m³).

La valeur de la contrainte critique d'entrainement peut être déterminée en écrivant le bilan des forces qui s'appliquent sur une particule solide posée au fond (voir figure 3).

Figure 3 : Équilibre des forces s'exerçant sur une particule solide posée sur le fond d'un canal soumis à un écoulement ; Source : Degoutte ().

Cette approche théorique est cependant très difficile à appliquer en pratique, en particulier du fait de la diversité des formes des particules, lesquelles conditionnent la valeur des forces en présence (voir Contrainte critique d’entrainement (HU)). On se contente donc le plus souvent de modèles empiriques (qui reposent d'ailleurs souvent sur des particules idéalisées, par exemple sphériques), le plus connu étant le diagramme de Shields.

Bibliographie :

Degoutte, J. () : Transport solide en hydraulique fluviale ; chapitre 2 ; 22p. ; disponible sur https://vicoin.portail-bassins-versants.fr/IMG/pdf/transport_solide_en_hydraulique_fluviale.pdf
Oms, C. (2004) : Localisation, nature et dynamique de l'interface eau-sédiment en réseau d'assainissement unitaire ; Thèse ENPC ; Partie II. Étude du taux de cisaillement en réseau d’assainissement unitaire ; 40p. ; disponible sur https://pastel.archives-ouvertes.fr/tel-00005725/file/partie_II_Cisaillement.pdf

Pour en savoir plus :

https://pastel.hal.science/tel-00005725/file/partie_II_Cisaillement.pdf

@@ Ligne 39 : / Ligne 39 : @@
 ==Contrainte de cisaillement sur les parois et lien avec les pertes de charge==
-Considérons un canal de forme quelconque et un écoulement uniforme à surface libre (''figure 3'').
+Considérons un canal de forme quelconque et un [[Ecoulement uniforme (HU)|écoulement uniforme]] à [[Ecoulement à surface libre (HU)|surface libre]] (''figure 3'').
-[[File:contrainte_cisaillement1_JV.png|600px|center|thumb|<center>''<u>Figure 3</u> : Les forces qui s'appliquent sur le volume de contrôle (en bleu) sont le poids, W, les forces de frottement sur le fond et les parois, F, et les forces de pression (qui s'annulent si l'écoulement dans le cas d'un régime uniforme).''</center>]]
+[[File:contrainte_cisaillement1_JV.png|600px|center|thumb|<center>''<u>Figure 3</u> : Les forces qui s'appliquent sur le volume de contrôle (en bleu) sont le poids, <math>W</math>, les forces de frottement sur le fond et les parois, <math>F</math>, et les forces de pression (qui s'annulent dans le cas d'un régime uniforme).''</center>]]
-Dans le cas d'un régime uniforme, un volume de contrôle est simplement soumis à son poids et aux forces de frottement (aucune accélération, et annulation des forces de pression du fait de sa répartition hydrostatique). La composante du poids parallèle à l'écoulement équilibre donc exactement les forces de frottement. On peut donc écrire la relation (3), en projetant ces forces sur un axe parallèle à l'écoulement :
+Dans le cas d'un régime uniforme, un volume de contrôle est simplement soumis à son poids et aux forces de frottement (il n'y a aucune accélération et les forces de pression s'annulent du fait de la répartition hydrostatique de cette dernière). La composante du poids parallèle à l'écoulement équilibre donc exactement les forces de frottement. On peut donc écrire la relation (3), en projetant ces forces sur un axe parallèle à l'écoulement :
-<center><math>F + Wx = 0 \qquad (3)</math></center>
+<center><math>F + W_x = 0 \qquad (3)</math></center>
-La composante <math>Wx</math> du poids s’exprime par la relation (4) :
+La composante <math>W_x</math> du poids s’exprime par la relation (4) :
-<center><math>Wx = ρ.g.L.S.sin(α) \qquad (4)</math></center>
+<center><math>W_x = ρ.g.L.S.sin(α) \qquad (4)</math></center>
@@ Ligne 59 : / Ligne 59 : @@
 * <math>ρ</math> : masse volumique du fluide (kg/m<sup>3</sup>),
 * <math>g</math> : accélération gravitationnelle (m/s<sup>2</sup>),
-* <math>S</math> : surface de passage de l’écoulement (m<sup>2</sup>),
+* <math>S</math> : [[Section mouillée (HU)|section mouillée]] (m<sup>2</sup>),
 * <math>L</math> : longueur du volume de contrôle (m),
-* <math>α</math> ; angle entre le fond du canal et l'horizontale.
+* <math>α</math> : angle entre le fond du canal et l'horizontale.
-La surface de frottement, <math>A</math>, est égale au produit du périmètre mouillé, <math>P</math> (longueur du contact entre le fluide et les parois dans une section mouillée) par la longueur de frottement, <math>L</math>, soit :
+La surface de frottement, <math>A</math>, est égale au produit du [[Périmètre mouillé (HU)|périmètre mouillé]], <math>P</math> (longueur du contact entre le fluide et les parois dans une section mouillée) par la longueur de frottement, <math>L</math>, soit :
 <center><math>A = P.L  \qquad (5)</math></center>
-Comme l'angle <math>α</math> est petit, on peut assimiler <math>sin(α)</math> à la pente I du canal et obtenir la relation (6) qui permet le calcul de la contrainte de cisaillement sur les parois, <math>τ_w</math> :
+Comme l'angle <math>α</math> est petit, on peut assimiler <math>sin(α)</math> à la pente <math>I</math> du canal et obtenir la relation (6) qui permet le calcul de la contrainte de cisaillement sur les parois ou sur le fond, <math>τ_w</math> :
@@ Ligne 76 : / Ligne 76 : @@
 avec :
-* <math>R_h</math> : rayon hydraulique (R_h = \frac{S}{P}) (m).
+* <math>R_h</math> : rayon hydraulique (<math>R_h = \frac{S}{P}</math>) (m).
-Cette relation peut être rapprochée de la formule permettant le calcul des pertes de charge, <math>J</math>, dans le cas d'un régime uniforme (voir [[Coefficient de rugosité (HU)]]) :
+Cette relation peut être rapprochée de la formule permettant le calcul des [[Perte de charge (HU)|pertes de charge]], <math>J</math>, dans le cas d'un régime uniforme (voir [[Coefficient de rugosité (HU)]]) :
@@ Ligne 88 : / Ligne 88 : @@
 * <math>g</math> : accélération de la pesanteur (m/s<sup>2</sup>) ;
 * <math>J</math> : pertes de charge par unité de longueur (m/m) ;
-* <math>V</math> : vitesse moyenne de l'écoulement (m/s).
+* <math>V</math> : [[Vitesse d'un écoulement (HU)|vitesse moyenne de l'écoulement]] (m/s).
-Comme en régime uniforme <math>I = J,</math> il existe donc une relation directe entre la vitesse moyenne d'écoulement et la contrainte de cisaillement au voisinage des parois (relation (8)) :
+Comme en régime uniforme <math>I = J</math>, il existe donc une relation directe entre la vitesse moyenne de l'écoulement et la contrainte de cisaillement au voisinage des parois (relation (8)) :

Contrainte de cisaillement (HU) : Différence entre versions

Version du 23 octobre 2023 à 14:14

Contrainte de cisaillement en mécanique des fluides

Contrainte de cisaillement sur les parois et lien avec les pertes de charge

Utilisation en transport solide

Affichages

Outils personnels