Nash-Sutcliffe (critère de) (HU) : Différence entre versions

Version actuelle en date du 10 avril 2024 à 18:38

Traduction anglaise : Nash-Sutcliffe criteria

Dernière mise à jour : 10/04/2024

Critère souvent utilisé pour caler au mieux un modèle hydrologique ou évaluer sa performance ; on doit plutôt parler du critère de Nash-Sutcliffe, en citant les noms des deux auteurs de la méthode (Nash et Sutcliffe, 1970) plutôt que du critère de Nash comme on le fait souvent.

[modifier] Formulation du critère

Le critère de Nash-Sutcliffe s’écrit sous la forme suivante :

Avec :

• $ S_{ob} $ et $ S_c $ : Valeurs observées et calculées au i^eme pas de temps ;
• $ Δt $ : pas de temps de la série chronologique discrétisée ;
• $ S_{mob} $ : moyenne arithmétique des observations.

[modifier] Intérêt du critère

Le critère de Nash-Sutcliffe est fondé sur la somme des carrés des écarts entre les valeurs observées et les valeurs simulées. Il a été bâti de façon à permettre la comparaison entre des événements présentant des ordres de grandeur de débits différents.

L'écart quadratique (somme des carrés des écarts) présente en effet l'inconvénient d'être d'autant plus grand que le débit moyen de l'événement est important. L'idée de Nash et Sutcliffe (1970) a donc consisté à le normer en divisant la somme des carrés des écarts par la variance des débits observés.

Sous sa forme classique (relation (1)), son interprétation est simple :

• une valeur nulle signifie que la modèle ne donne pas de meilleur résultat qu'un modèle basique donnant à chaque pas de temps un débit constant égal à la moyenne des débits observés ;
• une valeur positive signifie que le modèle donne de meilleurs résultats et qu'il est d'autant meilleur que le critère se rapproche de 1 ;
• une valeur négative est le signe d'une inadaptation du modèle.

[modifier] Limites et biais possibles

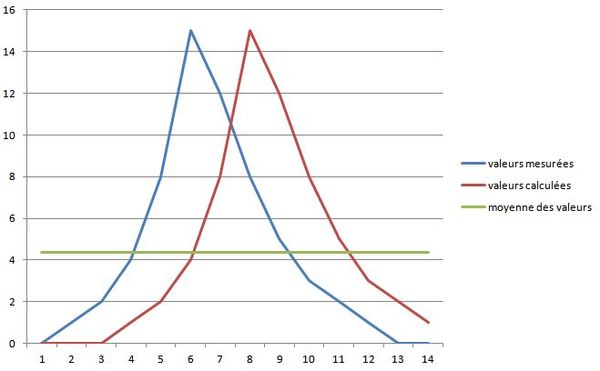
Malgré son intérêt, le critère de Nash-Sutcliffe n'est pas dénué de biais possibles. Par exemple, l'un de ceux-ci est lié au manque de synchronisation des valeurs mesurées et des valeurs calculées. Il est illustré par l'exemple de la figure 1 dans lequel les valeurs calculées sont strictement égales aux valeurs mesurées mais décalées de deux pas de temps.

Figure 1 : Exemple fictif : valeurs calculées égales aux valeurs mesurées mais décalées de deux pas de temps.

La valeur du critère de Nash-Sutcliffe correspondante est égale à -0,12. La simulation est donc supposée être de moins bonne qualité que le simple report de la valeur moyenne (en vert sur la figure).

Ce biais peut facilement être corrigé en décalant progressivement l'hydrogramme simulé jusqu'à ce que l'on maximise la valeur du critère. On peut alors évaluer la qualité de la représentation en utilisant deux critères : la valeur optimum du critère de Nash-Sutcliffe et la valeur du décalage (Semsar, 1995).

Cet exemple montre cependant combien il est dangereux de faire confiance à un critère unique pour caler un modèle ou juger de sa qualité.

Bibliographie

• Nash, J. E. , Sutcliffe, J. V. (1970) : River flow forecasting through conceptual models : part I-A : discussion of principles ; Journal of Hydrology ; 10 ; pp 282-290
• Semsar, A.A. (1995) : Mise au point d'une méthodologie d’évaluation et de comparaison des modèles de simulation hydraulique des réseaux d'assainissement ; thèse de doctorat ; INSA Lyon.