Coefficient de rugosité (HU)

Traduction anglaise : Roughness coefficient, Resistance coefficient, Friction factor

Dernière mise à jour : 30/4/2020

Coefficient caractérisant la plus ou moins grande résistance qu’un tronçon oppose au passage de l’eau.

Ce coefficient traduit globalement le rôle des forces de frottement externes dues à la rugosité des parois mais également internes liées à la viscosité du liquide. Il conditionne les pertes de charge et constitue un paramètre déterminant du calcul de la vitesse des écoulements.

Éléments d'historique

Les travaux fondateurs

Déterminer la capacité de transport d’un canal, d’un aqueduc ou d’un bief de cours d’eau a été, de tout temps, l’une des préoccupations majeures des hydrauliciens et des hydrologues. Déjà, dans l’antiquité, on attribuait à Héron d’Alexandrie (sans doute entre les années 65 et 150 de notre ère) d’avoir énoncé, le premier, que le débit dans une section d’écoulement résultait du produit de la section par la vitesse moyenne de l’eau dans cette section. Cette notion élémentaire d’hydraulique fut cependant longtemps ignorée. La principale difficulté de son usage résultant de la détermination de la vitesse moyenne. C’est seulement vers la fin du XVIIIème siècle que furent produites les premières formulations pratiques, développées ultérieurement au XIXème et au début du XXème siècles.

Dans le cadre de l’amélioration du système d’alimentation en eau de Paris, Antoine Chezy (1718-1798) établit en 1775 que la vitesse moyenne $ V $ d’un écoulement permanent répondait à la relation (1) :

$ V = C.\sqrt{R_h.I} \quad (1) $

avec :

• $ Rh $ : rayon hydraulique de l’écoulement ($ m $) ;
• $ I $ : pente du radier du canal ($ m/m $) ;
• $ C $ : coefficient dit de Chezy ($ m^{1/2}/s $).

Cette équation résultait de l’hypothèse d’égalité, en régime permanent, entre les forces "motrices" dues à la gravité, et les forces de frottement sur les parois du canal. Chezy avait, par ailleurs conscience que le coefficient $ C $ n’était pas constant et pouvait varier d’un bief à l’autre. Cette formulation remarquable resta cependant assez confidentielle. Elle fut exhumée des archives de l’École nationale des ponts et chaussées (dont Chezy fut le second Directeur) plus d’un siècle plus tard, et publiée aux Etats-Unis par G. Herschel en 1897.

Dans l’équation (1) le coefficient C traduit donc globalement la dissipation de l’énergie par frottement sur les parois et contient implicitement les effets dus à la rugosité de celles-ci. A la même époque, sans pour autant connaître les travaux de Chezy, G. Du Buat (1738-1809) appliquant le même principe d’égalité des forces de pesanteur et de frottement, proposa une formulation considérée par lui comme "universelle", car elle reposait sur l’hypothèse que les frottements étaient uniquement dus à la viscosité du fluide et non à la rugosité des parois.

Le XIXème siècle

Avec l'accroissement des activités industrielles et le développement de l’aménagement des territoires, de très nombreux ingénieurs et chercheurs vont, dans cette période, travailler à l’élaboration de formules de calcul de vitesses d’écoulement. Les premiers reprirent l’hypothèse de Du Buat sur la seule contribution de la viscosité, ou les travaux de A. De Coulomb (1736-1806) sur les forces de résistance à l’avancement d’un solide dans un liquide. P. Girard en 1803, G. De Prony en 1804, mais aussi l’Allemand Eytelwein en 1818, proposèrent ainsi des formules du type :

$ R_h.I = a.V + b.V^2 + ... \quad (2) $

Par exemple la formule d’Eytelwein, très populaire en Europe s’écrivait sous la forme :

$ R_h.I = 2{,}4.10^{-5}.V + 3{,}66.10^{-4}.V^2 \quad (3) $

Pour des vitesses de l’ordre du m/s la relation (3) pouvait alors se réduire à la formule suivante :

$ V ≈ 50.\sqrt{R_h.I} \quad (4) $

Cette formule fut proposée pour la première fois vers 1830 par l’italien Tadini. Elle fut confirmée en 1850 par le français E. Courtois. Selon le même principe, et devant les fluctuations expérimentales du coefficient $ C $, divers auteurs introduisirent des éléments correctifs censés tenir compte de divers effets liés à la géométrie des canaux comme la courbure des biefs. Barré de Saint Venant proposa sa propre formule vers 1850 sous la forme :

$ V = 60.(R_h.I)^{11/21} \quad (5) $

En réalité, ce furent les expériences conduites par le français Henri Darcy (1803-1858) et son assistant Henry Bazin (1829-1917) sur des canaux artificiels constitués de divers matériaux qui mirent en évidence le rôle fondamental de la nature des parois dans la variabilité du coefficient $ C $ de la formule de Chezy. La notion de rugosité de paroi était désormais admise. En 1865 fut ainsi proposée la relation :

$ V^2 = \frac{R_h.I}{a.(1+\frac{b}{R_h})} \quad (6) $

dans laquelle $ a $ et $ b $ étaient des coefficients dépendant de la nature des parois des canaux. Cette formule connut un succès considérable et de nombreux expérimentateurs tentèrent d’en vérifier sa validité dans le cas, notamment, de cours d’eau naturels. Les travaux de synthèse les plus élaborés furent dus à 2 ingénieurs suisses : E. Ganguillet (1818-1894) et W. Kutter (1818-1888), qui proposèrent, en 1869, la formulation suivante du coefficient de Chezy $ C $.

$ C = \frac{a+\frac{1}{n}}{1+a.\frac{n}{\sqrt{R_h}})} \quad (7a) $

Avec :

$ a=23+\frac{1{,}55.10^{-4}}{I} \quad (7b) $

• $ n $ : coefficient de rugosité.

Les formules(7a) et (7b) présentaient l’avantage de ne comprendre qu’un seul coefficient. Au demeurant elle était jugée compliquée et les chercheurs tentèrent de la simplifier. Ainsi Kutter proposa-t-il une version simplifiée de ces relations.

$ C = \frac{100.\sqrt{R_h}}{n+R_h} \quad (8) $

Kutter proposait également un tableau pour choisir la valeur du coefficient $ n $ (tableau 1).

Tableau 1 : Valeurs à attribuer au coefficient $ n $ dans la formule de Kutter.

En 1869, l’ingénieur des Ponts et chaussées P. Gauckler (1826-1905) proposa les relations suivantes :

$ V = a_1.R_h^{4/3}.I \quad pour I < 7.10{-4}\quad (9) $ $ V = a_2.R_h^{2/3}.I^{1/2} \quad pour I ≥ 7.10{-4}\quad (10) $

La relation (10), combinée avec la relation de Chézy (1) est équivalente à celle qui sera proposée vingt ans plus tard par R. Manning (1816-1897) soit :

$ C = \frac{1}{n}.R_h^{1/6}\quad (11) $

Cette dernière formule connut un succès considérable. Elle est d’ailleurs encore en usage aujourd’hui. Malgré ce succès, Manning n’en était pas satisfait lui-même considérant que les dimensions de l’équation de Chezy, avec le coefficient de l’équation (11), n’étaient pas homogènes. Il proposa par la suite, une nouvelle expression en introduisant, notamment, la pression atmosphérique afin d’obtenir une équation de Chezy correctement dimensionnée. Cette relation était :

$ C = 34.\left[1+\frac{\sqrt{R_h}}{4}-\frac{0{,}03}{\sqrt{R_h}} \right]\quad (12) $

En réalité cette dernière équation ne fit pas d’adeptes. En 1890 le Français A. Flamant recommanda l’utilisation de la relation (11) comme beaucoup d’autres ingénieurs européens. La célèbre formule de Manning (établie en fait pour la première fois par Gauckler) est souvent associée au suisse A. Strickler. Ce dernier s’est en particulier intéressé au coefficient $ n $ de rugosité de Manning et a proposé, pour le cas des canaux en terre ou des fonds sableux, la relation :

$ n = 0{,016.d^{1/6}}\quad (13) $

avec :

• $ d $ : diamètre des grains ($ mm $)

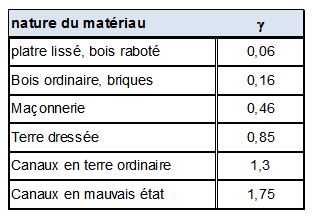
En 1897, conscient des difficultés d’utilisation de la relation (6), H. Bazin proposa une formule restée très populaire en France :

$ C = \frac{87}{1+γ.\sqrt{R_h}}\quad (14) $

Il proposa également différentes valeurs pour le coefficient γ (voir le tableau 2).

Tableau 2 : Valeurs à attribuer au coefficient $ γ $ dans la formule de Bazin.

L'hydraulique moderne

L’inconvénient majeur des diverses formules proposées tout au long du XIXème siècle était bien sûr leur caractère empirique et leur prise en compte globale, par le biais de coefficients, de multiples phénomènes comme la viscosité du fluide, la rugosité des parois, le transport solide et le charriage sur le fond, etc.. En outre, comme l’indiquait Manning, les formules n’étaient pas correctement dimensionnées.

Afin d’assurer à l’équation de Chezy, des dimensions homogènes on peut écrire :

$ C = \sqrt{\frac{8.g}{λ}}\quad (15) $

soit :

$ V = \sqrt{\frac{8.g.R_h.J}{λ}}\quad (16) $

Avec :

• $ g $ : accélération de la pesanteur ($ m/s^2 $) ;
• $ J $ : pente de la ligne d'énergie ou pertes de charge par unité de longueur ($ m/m $) ;
• $ λ $ : coefficient sans dimension appelé coefficient de frottement, ou coefficient universel de pertes de charge dans l’hydraulique des conduites en charge.

Nota 1 : Dans le cas d'un écoulement permanent uniforme $ I=J $.

Nota 2 : L'intérêt de cette formulation est d'établir une relation valable aussi bien pour les écoulements en charge que pour les écoulements à surface libre. Ce sont d’ailleurs les résultats des recherches dans le domaine des écoulements en charge qui ont beaucoup contribué à l'élaboration des formules de débit des écoulements à surface libre. Ceci est particulièrement intéressant pour les écoulements dans les conduites d'assainissement qui peuvent se produire à surface libre ou en charge.

Avec cette formulation il devenait possible de faire porter l’ajustement des formules de débit sur le coefficient $ λ $ en explicitant de façon distincte le rôle de la viscosité du fluide et celui de la rugosité des parois. Ce sont les recherches sur la turbulence, au début du XXème siècle qui donnèrent lieu aux résultats les plus significatifs. Les chercheurs se sont particulièrement intéressés aux relations entre $ λ $ et le nombre de Reynolds $ R_e $.

$ R_e = \frac{4.V.R_h}{ν}\quad (17) $

Avec :

• $ ν $ : Viscosité cinématique du fluide ($ m^2/s $)

Si les travaux de L. Prandtl et Von Karman sur la turbulence, dans les années 20, sont souvent considérés comme les bases de l’hydraulique moderne, de nombreux expérimentateurs comme Moody, Nikuradze, Colebrook et White contribuèrent à la production de formules très utilisées aujourd’hui, notamment dans l’hydraulique des conduites en charge.

La relation la plus intéressante dans ce contexte est celle proposée par Colebrook et White qui présente l'avantage d'être valable pour tous les écoulements turbulents (turbulents lisses, turbulents rugueux et zone de transition).

$ \frac{1}{\sqrt{λ}} = -2.log\left[\frac{k}{a.R_h}+\frac{b}{R_e.\sqrt{λ}} \right] \quad (18) $

avec :

• $ λ $ : coefficient de Colebrook (sans dimension) ;
• $ g $ : accélération de la pesanteur ($ m/s^2 $) ;
• $ k $ : rugosité des parois ($ m $) ;
• $ R_h $ : rayon hydraulique ($ m $) ;
• $ ν $ : viscosité cinématique du fluide ($ m^2/s $) ;
• $ a $ et $ b $ : coefficients sans dimension (12 < $ a $ < 15 et 0 < $ b $ < 6).

Il s'agit d'une relation implicite qui paraît très compliquée à manipuler. Cependant, Chocat (1978) a montré qu'il était possible d'en déduire une expression explicite de la constante $ C $ de la formule de Chézy dans le cas d'un écoulement uniforme ($ I=J $).

D'après la relation (16) :

$ V = \sqrt{\frac{8.g.R_h.J}{λ}} = \sqrt{\frac{8.g.R_h.I}{λ}}\quad (19) $

On peut donc écrire :

$ I = λ.\dfrac{V^2}{8.g.R_h} \quad\quad \Longrightarrow \quad\quad \dfrac{1}{\sqrt{\lambda}} = \dfrac{V}{\sqrt{8.g.R_h.I}} \quad(20) $

En reportant les expressions (17) et (20) dans la relation (18), on obtient une formulation explicite de $ λ $ :

$ \dfrac{1}{\sqrt{λ}} = -2.log\left[\frac{k}{a.R_h}+\frac{b.ν}{8.R_h\sqrt{2.g}.\sqrt{R_h.I}}\right] \quad (21) $

La relation (20) permet également d'écrire :

$ V = \dfrac{1}{\sqrt{λ}}.\sqrt{8.gR_h.I} = C.\sqrt{R_h.I} \quad(22) $

avec

$ C = \dfrac{1}{\sqrt{λ}}\sqrt{8.g} \quad(23) $

En reportant la relation (21) dans l'expression (23), on obtient finalement une expression explicite du coefficient $ C $ de Chezy :

$ C = -4\sqrt{2.g}.log \left[\frac{k}{a.R_h}+\frac{b.ν}{8.R_h\sqrt{2.g.R_h.I}}\right] \quad(24) $

Les valeurs généralement retenues pour $ a $ et $ b $ (Chocat, 1978) sont les suivantes :

• $ a = 14{,}8 $
• $ b = 2{,}51 $

De façon pratique, l'intérêt de cette relation est de faire apparaître des grandeurs physiques mesurables (la viscosité du fluide et la taille moyenne des aspérités du fond et des parois). Il est cependant important de comprendre que dans un réseau d'assainissement les pertes de charge linéaires dépendent non seulement de la dimension des aspérités, mais également des macro-obstacles à l'écoulement que l'on peut y rencontrer : coudes, chutes, câbles accrochés aux parois, branchements, etc..

La valeur de k doit donc être majorée pour tenir compte de ces éléments. A titre indicatif, le tableau suivant donne des indications sur le choix de $ k $ et de $ ν $ :

Valeurs indicatives pour le choix de $ ν $ et $ k $.

Bibliographie :

• Carlier, M. (1972) : Hydraulique générale et appliquée ; Eyrolles ; Paris ; 565 p.
• Chocat, B. (1978) : Un modèle de simulation des écoulements dans les réseaux d'assainissement pluvial ; thèse Docteur ingénieur ; INSA Lyon ; 304p.
• Lautrich, R. (1971) : Tables et abaques pour le calcul hydraulique des canalisations sous pression, égouts et caniveaux ; Eyrolles ; 1971.
• Winghart, M. : Cours polycopié de mécanique des fluides et d'hydraulique ; INSA de Lyon - département GCU.