Débit (HU)

Traduction anglaise : Discharge, Flow

Dernière mise à jour : 31/3/2020

Volume d'eau qui s'écoule en un point donné pendant une durée donnée à travers une section droite donnée d’un écoulement.

Les unités les plus courantes sont le m³/s, le L/s ou le m³/h. En hydrologie, comme en hydraulique, la mesure du débit relève de la débitmétrie.

Une grandeur difficile à appréhender

Le caractère d'évidence de la définition précédente cache en fait deux difficultés de taille :

• La première difficulté est d'ordre métrologique. Comment mesurer un volume d'eau écoulé pendant une certaine durée ? Si le débit dans la rivière ou dans la conduite est faible on peut essayer de détourner tout le flux vers un récipient de volume connu et mesurer le temps nécessaire pour le remplir. Mais dès que le débit devient plus important, ce type de méthode devient bien évidemment impossible à mettre en œuvre. Voir Débitmétrie.
• La seconde difficulté est plus fondamentale. Le débit est une grandeur qui varie avec le temps. Quelle doit être la durée d'observation ? une seconde ? une heure ? une année ?

Pour résoudre ces deux difficultés, on est en fait amené à distinguer le débit instantané et le débit moyen..

Débit instantané

Le débit instantané est théoriquement celui qui correspond à une durée d'observation tendant vers zéro. En pratique, on en donne une définition différente utilisant la notion de vitesse d'écoulement. Ainsi, si $ V(x, y) $ représente la vitesse d'écoulement au point de coordonnées $ x $ et $ y $ dans une section transversale $ S $, le débit instantané $ Q_i $ peut être défini par la relation :

$ Q_i=\iint_S{V(x,y).dx.dy}\quad(1) $

Cette nouvelle définition du débit présente l'intérêt d'être plus claire que la précédente (l'ambiguïté sur le temps étant levée), mais également plus proche des techniques métrologiques. La vitesse de l'eau est en effet une quantité mesurable. Ainsi, si l'on mesure la vitesse moyenne de l'écoulement ($ V_j $) au travers de n petites surfaces $ S_j $, le débit instantané peut être évalué par la relation :

$ Q_i=\sum_{j=1}^n{V_j.S_j}\quad(2) $

Enfin, en introduisant la notion de vitesse moyenne de l'écoulement ($ V_m $) qui pour certains types d'écoulement peut être calculée en fonction de paramètres physiques, on peut écrire :

$ Q_i=V_m.S\quad(3) $

où $ S $ est la surface de la section transversale (section mouillée) :

$ S=V_m.\sum_{j=1}^n{S_j}\quad(4) $

Figure 1 : Exemple d'évolution des débits de temps sec sur une semaine mesurés au pas de temps de 6mn.

Débit moyen

Ayant défini le débit instantané, il est maintenant possible de calculer des débits moyens. Le débit moyen $ Q_m(d) $ sur une période d'observation $ d $ peut ainsi être calculé par la relation :

$ Q_m(d)=\frac{1}{d}.\int_{t_0}^{t_0+d}{Q_i(t).dt}\quad(5) $

Selon la valeur de $ t_o $ (date du début des observations) et celle de $ d $ (durée des observations), une infinité de débits moyens peut être calculée.

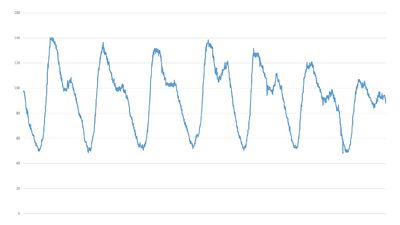
Dans le cas des réseaux d'eaux usées, on utilise souvent un débit moyen horaire, ou un débit moyen journalier. Les variations du débit en fonction du temps sont souvent mises en évidence en traçant un hydrogramme journalier.

Caractérisation des rivières

Pour caractériser l'importance d'une rivière, on utilise la notion de module. Le module d'une rivière est égal au débit moyen calculé pour une durée d'observation $ d $ très grande (la plus grande possible) et égale à un nombre entier d'années. Le module est en fait égal à la moyenne des débits moyens annuels sur la période $ d $.

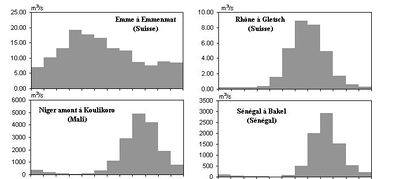
Pour mettre en évidence le régime de la rivière (variations saisonnières des débits), les géographes visualisent les variations annuelles moyennes des débits mensuels moyens sous la forme d'un diagramme (voir figure 2).

</center>Figure 2 : Régimes moyens (en m³/s) de quelques fleuves dans le monde ; Source  : cours hydrologie EPFL.</center>