Diagramme de Shields (HU)

Traduction anglaise : Shields diagram

Dernière mise à jour : 24/10/2023

Diagramme permettant de calculer le seuil de mise en mouvement d’une particule dans un écoulement liquide et qui sert encore de base à la plupart des calculs de contrainte critique d'entraînement.

Éléments d'historique

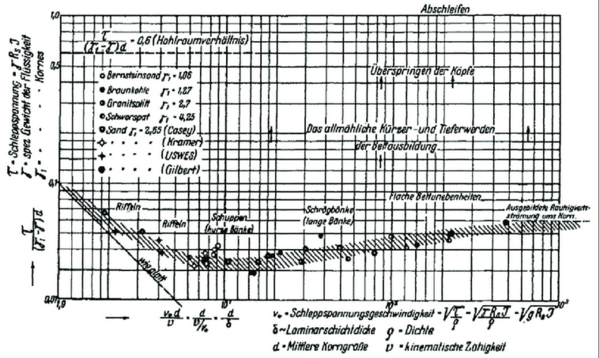
La première version du "diagramme de Shields" (voir figure 1) a été construit par Shields (1936) en utilisant des données expérimentales acquises en laboratoire par l’auteur ainsi que des données expérimentales publiées antérieurement par Gilbert (1914), Kramer (1932) et Casey (1935), ainsi que rapporté par Kennedy (1995).

Figure 1 : Diagramme originel de Shields ; Source : Shield (1936).

Les tribulations de Shields entre les États-Unis et l’Allemagne des années 1930 où il mena, non sans difficulté, ses travaux en transport solide, son retour aux États-Unis, son pays d’origine, pour une carrière d’ingénieur dans l’industrie, puis le grand succès des résultats de son travail de doctorat, notamment du fait de Hunter Rouse (1950), ont contribué à la renommée voire à la "légende" d'Albert Shields (Kennedy, 1995 ; Buffington, 1999).

En tout état de cause, son approche sert encore de base à la plupart des calculs de contrainte critique pour la mise en mouvement des particules au fond d'un canal, d'une rivière ou d'une conduite.

Mode construction du diagramme de Shields

Le diagramme de Shields repose sur l'utilisation de 3 nombres sans dimension (voir Contrainte critique d’entrainement (HU)) :

• le rapport des masses volumiques : $ ρ* $ (relation (1)) ;
• le nombre de Reynolds particulaire : $ Re_* $ (relation (2)) ;
• la contrainte adimensionnelle de cisaillement ou nombre de Shields : $ θ $ (relation (3)).

$ ρ* = \frac{ρ_s-ρ}{ρ}\qquad (1) $

$ Re_* = \frac{ρ.u_*d}{μ}= \frac{ρ^{1/2}.τ_w^{1/2}.d}{μ}\qquad (2) $

$ θ = \frac{ρ.u_*^2}{(ρ_s-ρ).g.d}= \frac{ρ*.u_*^2}{g.d}= \frac{τ_w}{(ρ_s-ρ).g.d}\qquad (3) $

Avec :

• $ τ_w $ : contrainte de cisaillement près du fond ou des parois (N/m²),
• $ d $ : dimension caractéristique des particules (m),
• $ ρ $ : masse volumique du fluide (kg/m³),
• $ ρ_s $ : masse volumique des particules (kg/m³),
• $ g $ : accélération gravitationnelle (m/s²),
• $ u_* $ : vitesse de frottement (m/s),
• $ μ $ : viscosité dynamique (kg/m/s).

Il représente graphiquement l'évolution de la contrainte critique d'entraînement en fonction du nombre de Reynolds particulaire.

Principes de construction

Les travaux expérimentaux de Shields (1936) servent encore de base à la plupart des calculs de contrainte critique pour la mise en mouvement des particules au fond d'un canal, d'une rivière ou d'une conduite. Le critère de Shields permet par exemple de calculer le frottement critique dans le cas d’un écoulement permanent, sur un fond plat horizontal.

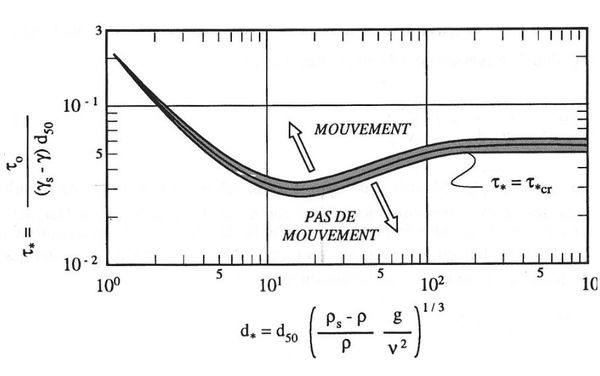
Nous utiliserons ici la représentation modifiée par Yalin (1977), plus facile à utiliser (Figure 1). Ce diagramme permet de calculer la valeur d'une tension adimensionnelle de frottement critique $ τ_* $ en fonction d'un diamètre adimensionnel de particule $ d_* $.

Figure 1 : Diagramme de Shields-Yalin.

$ τ_* $ et $ d_* $ s'expriment de la façon suivante :

$ d_*=d.\left(\frac{ρ_s-ρ}{ρ}.\frac{g}{ν^2}\right)^{1/3} $

$ τ_*=\frac{ρ_s-ρ}{ρ}.\frac{R_h.J}{d} $

Avec :

• $ ρ $ : masse volumique de l'eau (kg/m³) ;
• $ ρ_s $ : masse volumique de la particule (kg/m³) ;
• $ ν $ : viscosité cinématique de l'eau (m²/s) ;
• $ R_h $ : rayon hydraulique de l'écoulement (m) ;
• $ d $ : diamètre de la particule (m) ;
• $ g $ : accélération de la pesanteur (m/s²) ;
• $ J $ : Pente de la ligne d'énergie (m/m).

Nota : Le rapport moyen entre la masse volumique moyenne des sables et celle de l'eau et de l'ordre de 2,6 et la viscosité cinématique de l'eau est de l'ordre de 1,3.10^-6, la valeur de $ d_* $ est donc de l'ordre de :

$ d_*=21 000.d $

Bibliographie :

• Buffington, J. (1999) : The legend of A. F. Shields ; Journal of Hydraulic Engineering ; 125(4) ; p.376-387.
• Buffington, J., Montgomery, D. (1997) : A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers ; Water Resources Research ; 33(8) ; p.1993-2029.
• Garcia, M. (2008) : Sedimentation engineering : processes, management, modeling and practice ; ASCE.
• Kennedy, J. (1995) : The Albert Shields story ; Journal of Hydraulic Engineering ; 121(11), p.766-772.
• Rouse, H. (1950) : Engineering hydraulics ; John Wiley & Sons.
• Shields, A. (1936) : Application of Similarity Principles and Turbulence Research to Bed-Load Movement. California Institute of Technology, Pasadena (Translate from German).
• Shvidchenko, A., Pender, G. (2000) : Flume study of the effect of relative depth on the incipient motion of coarse uniform sediments ; Water Resources Research ; 36(2) ; p.619-628.
• Van Rijn, L. (1984a) : Sediment transport, part I: bed load transport ; Journal of Hydraulic Engineering ; 110(10) ; p.1431-1455.
• Van Rijn, L. (1984b) : Sediment transport, part II: suspended load transport ; Journal of Hydraulic Engineering ; 110(11) ; p.1613-1638.
• Yalin, M.S. (1977) : Mechanics of sediment transport. 2nd ed. Pergamon Press, Oxford, UK. 360 pp

Pour en savoir plus :

• Dufrene, M., Isenmann, G. (2018) : Transport solide ; cours ENGEES ; disponible sur : https://drive.google.com/file/d/1gO97J6d9Xzg8tx17HPaReEpGVL7sZmMY/view