Méthode des volumes (HU)

Traduction anglaise : Volumes design method

Dernière mise à jour : 14/06/2021

Méthode simplifiée permettant de déterminer le volume de stockage des bassins de retenue ou autres ouvrages de stockage-infiltration. On parle parfois de méthode des courbes enveloppes.

Hypothèses de départ

La méthode repose sur les hypothèses suivantes :

• le débit de fuite de l'ouvrage de stockage est supposé constant ;
• il y a transfert instantané de la pluie à l'ouvrage de retenue ; les phénomènes d'amortissement dus au ruissellement sur le bassin sont donc négligés ; cela veut dire que cette méthode ne sera applicable que pour des bassins versants relativement petits ;
• les différentes grandeurs (débit de fuite et volume de l'ouvrage) sont adimensionnalisées en les divisant par la surface active du bassin versant, on raisonne ainsi en débit spécifique (de dimension $ L.T^-1 $) et en volume spécifique (qui a la dimension d'une hauteur d'eau $ L $).

Principes de la méthode

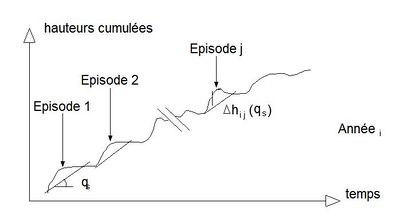
La méthode des volumes essaye de prendre en compte la distribution temporelle des apports dans l'ouvrage de stockage en utilisant un traitement voisin de la méthode des pluies appliqué à une série chronologique de pluies réelles observées. La figure 1 illustre graphiquement le traitement statistique effectué sur les données. On trace sur un graphe temporel le cumul des volumes (exprimées en hauteurs de pluie) produits successivement par chaque pluie ainsi que le cumul des volumes (également exprimés en hauteurs d'eau) évacués, avec l'hypothèse d'un débit de fuite constant tant qu'il y a de l'eau dans l'ouvrage. La vidange se termine donc que lorsque l'ouvrage est vide et plusieurs événements successifs peuvent se cumuler. La différence, à chaque instant, entre la hauteur produite et la hauteur évacuée: $ ΔH(t, qs) $ doit être stockée dans l'ouvrage.

Figure 1 : Courbe des hauteurs à stocker en fonction du temps

On peut en déduire la valeur maximum $ ΔHmax(i, qs) $, soit pour l'événement i si on raisonne par événement, soit pour la période de temps i si on raisonne par période de temps (par exemple par jour, par mois, par année). Le choix du mode de dépouillement (raisonner par événements ou par période de temps) conditionne les résultats et en particulier la façon d'en déduire un risque de dépassement d'une hauteur (i.e. d'un volume).

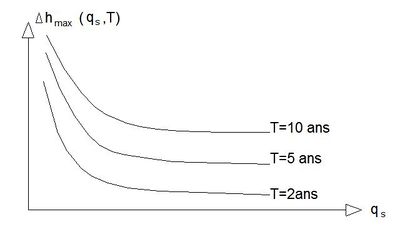
Une des façons les plus courantes d'effectuer ce traitement, qui est correcte pour les grandes périodes de retour (supérieure à 1 an), consiste à travailler par année. Pour chaque année i et pour chaque débit spécifique $ qs $ , on calcule ainsi la hauteur $ Δhmax(i, qs) $ qui représente la plus grande différence observée pendant l'année i entre la courbe des hauteurs apportées et celles des hauteur évacuées. On réalise ensuite le classement fréquentiel de ces valeurs maximales de façon à construire un graphe $ Δhmax (qs , T) $ en fonction de $ qs $ et $ T $ (voir la figure 2).

Figure 2 : Courbe des hauteurs à stocker en fonction du débit spécifique de vidange et de la période de retour

C'est cette méthode qui a été utilisée pour construire les abaques de l'Instruction technique de 1977 qui propose des courbes moyennes sur les grandes régions pluviométriques.

Intérêts et limites de la méthode des volumes

La méthode des volumes présente l'intérêt, par rapport à la méthode des pluies, de prendre en compte la répartition temporelle réelle des pluies dans le temps (à la fois en terme d'enchainements des événements et de forme des hyétogrammes). De ce fait elle conduit souvent à des volumes d'ouvrage un peu supérieur (de l'ordre de 5% à 15%), ce que l'on peut interpréter comme une correction de la sous-estimation due à la méthode des pluies.

Bibliographie :

• [Desbordes, 1975b] : Desbordes M. ; " Quelques méthodes de calcul des bassins de rétention des eaux pluviales. " ; Centre belge d’étude et de documentation des eaux ; N°377 ; Avril 1975.
• [Ministères, 1977] : Ministère de la culture et de l'environnement, Ministère de l'équipement et de l'aménagement du territoire, Ministère de l'agriculture, Ministère de la santé et de la sécurité sociale ; "Instruction technique relative aux réseaux d'assainissement des agglomérations" ; IT 77 284 INT ; Imprimerie nationale ; Paris ; 62 p + annexes ; 1977.

Voir aussi : Méthode des débits, Méthode des pluies.