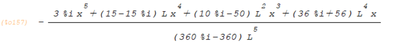Utilisateur:Jean-Michel Tanguy/SujetENTPE2021/CAILLOUX - CLORENNEC - VALLEAU

Contexte

Le changement climatique, causé par les activités humaines, accentue la dégradation des littoraux. Il est responsable de la hausse du niveau des mers et cause des tempêtes de plus en plus fréquentes et sévères. Le changement climatique accélère également l’érosion. Au cours du XXe siècle, le niveau de la mer s’est élevé de 18 cm à l'échelle mondiale.

Cette augmentation du niveau des océans est due à deux phénomènes causés par le changement climatique par plusieurs éléments tels que la fonte des glaces qui constitue un apport d’eau supplémentaire pour l’océan, ce qui fait augmenter son volume et par conséquent son niveau. Mais aussi la dilatation thermique car en effet plus l’eau est chaude, plus elle occupe un volume important à quantité égale, les molécules soumises à la chaleur ont tendance à s'agiter et à s'éloigner les unes des autres.

Le changement climatique par l’augmentation du niveau de la mer et des tempêtes plus fréquentes et plus sévères accélère : l’érosion marine, la mer érodent les rivages. Plus l’océan gagne du terrain sur la terre, plus il a de chance d’emporter avec lui du sable ou de fragiliser les roches, augmentant le risque d’éboulement. Ce phénomène d’érosion entraîne le recul du trait de côte dans de nombreuses régions du monde. De plus, cette augmentation peut également provoquer des inondations.

Fichier:Crozon.jpg

Bretagne

Le thème d’étude est la quantification de l’impact des houles sur le littoral. Le modèle le plus utilisé qui permet de modéliser les houles est le modèle de Berkhoff, une équation aux dérivées partielles, que nous résoudrons par une méthode analytique puis par homotopie.

Modèle de Berkhoff

Afin de modéliser la houle, et ce plus précisément qu'un simple cosinus ( comme ci-dessus) nous allons utiliser le modèle de Berkhoff. Il s'agit d'un modèle bi-dimensionnel qui a pour expression :

$ \boxed {\nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0} $

Avec

$ phi $ : Le potentiel

k : Le nombre d'onde

H: La profondeur

$ \omega $ : La fréquence

T: La période

C la célérité de l'onde

Cg : La célérité de groupe des vagues

Cette équation décrit l'effet combiné de la réfraction et de la diffraction sur la propagation de la houle, en particulier au niveau des zones portuaires. Nous nous placerons dans le domaine des ondes longues.

Simplification du problème  : C = Cg = $ \sqrt{gH} $. L'équation devient alors : Δ$ \phi $+$ k^2 $$ \phi $=0

En 1D on obtient : $ \frac{\partial^2 \phi}{\partial x^2} + k^{2}\phi=0 $

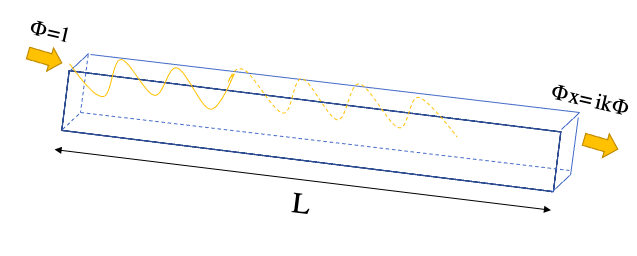
Cas n°1 : Canal monodimensionnel plat avec sortie libre

Solution analytique

On résout le modèle de Berkhoff simplifié en 1D : $ \frac{\partial^2 Φ}{\partial x^2} + k^{2}Φ=0 $

Par simplification on obtient l’équation du second degré suivante : $ r^{2}+k^{2}=0 $, Discriminant: $ Δ = -4k² $ avec $ r1=-ik $ et $ r2=+ik $

Donc la solution sera de la forme : $ Φ(x)=A \text{e}^{-ikx}+B \text{e}^{ikx} $, avec A,B réels

Déterminons A et B grâce aux conditions limites :

$ Φ(x=0)=1 $ d’où $ A+B=1 $ et $ Φ’(x=L)=ikΦ $ d’où $ B=0 $ et $ A=1 $

On a donc: $ \boxed{Φ(x)=\text{e}^{ikx}} $

Grâce au potentiel des vitesses Φ, on cherche h, la hauteur d'eau algébrique s'ajoutant à la hauteur d'eau moyenne H constante dans ce Cas n°1.

L'évolution dans le temps de la hauteur de houle est donnée par : $ h(x,t)=R(Φ\text{e}^{-iωt}) $= R($ \text{e}^{i(kx−ωt)} $) or $ H=R(ϕ) $

En conclusion, on a: $ \boxed{h(x,t)=\cos(kx-ωt)} $

Solution par la méthode d'homotopie

La relation d'homotopie s'écrit en choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle:

$ (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $

En injectant la décomposition en série entière $ \phi(x,p)=\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+p^3\phi_3(x)+... $ et sa seconde dérivée:

$ \phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+... $

Nous obtenons:

$ (1-p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+p^3\phi_3(x)+...)]=0 $

Il faut ensuite simplifier et écrire cette relation suivant les puissances de p croissantes. Cette relation étant valable quel que soit p, tous les coefficients devant les puissances de p sont donc nuls.

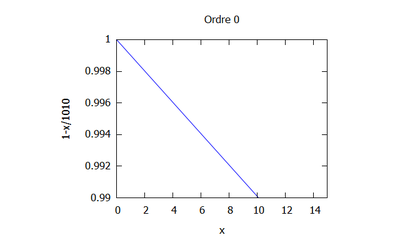
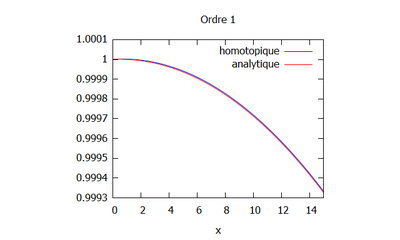
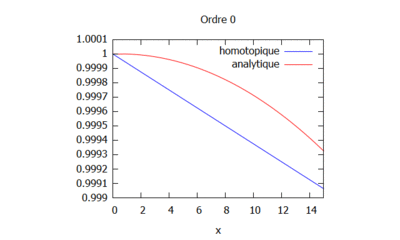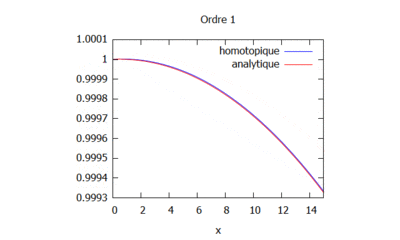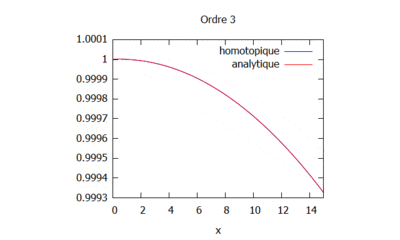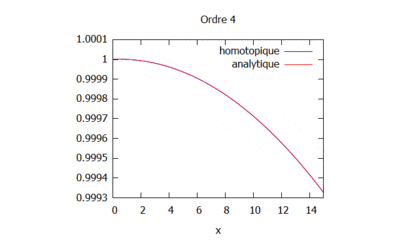
Ordre 0

$ \phi_{0,xx}=0 $ soit $ \phi_0=Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, il vient :

$ \boxed{\phi_0(x)=\dfrac{ikx}{1-ikL}x+1} $

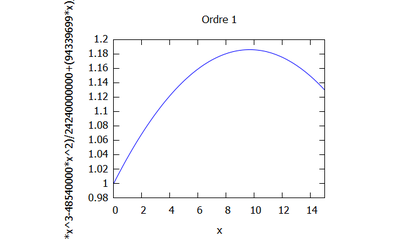
Ordre 1

$ \phi_{1,xx}-\phi_{0,xx}+\phi_{0,xx}+k^2\phi_0=0 $ soit $ \phi_{1}=-k^2\int\phi_0dxdx +Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $, il vient : $ \boxed{Φ(1)=- \dfrac{k^2L(k^2L^2+3ikL-3)} {3(1-ikL)^2}x-k^2\left (\dfrac{ik} {6(1-ikL)}x^3+\dfrac{1} {2}x^2 \right )} $

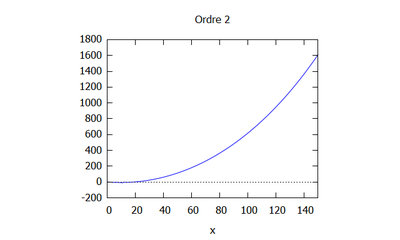
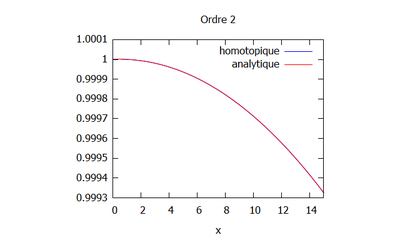
Ordre 2

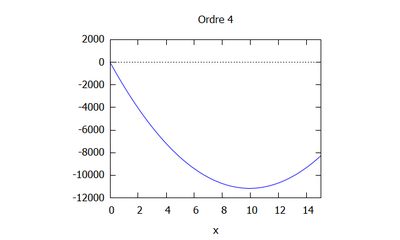
On effectue le calcul à l'ordre 2 avec maxima, avec comme hypothèses N=10 et k=1/L pour simplifier les calculs.

La valeur de h est :

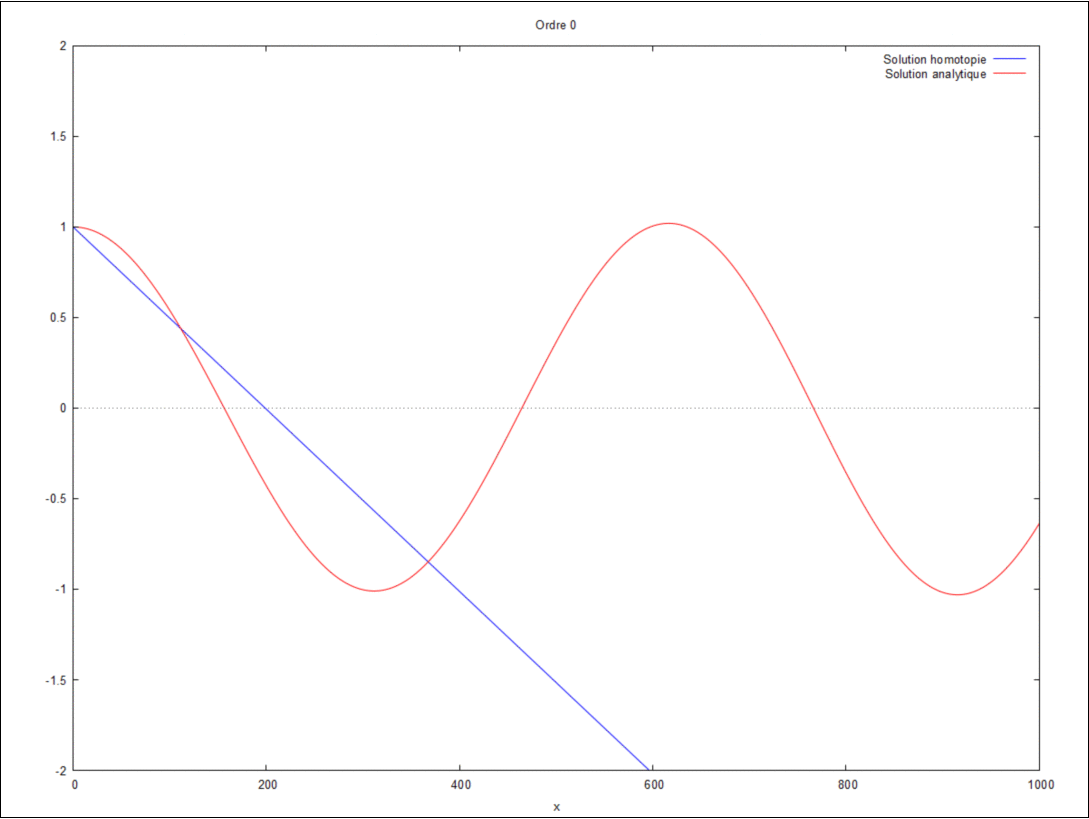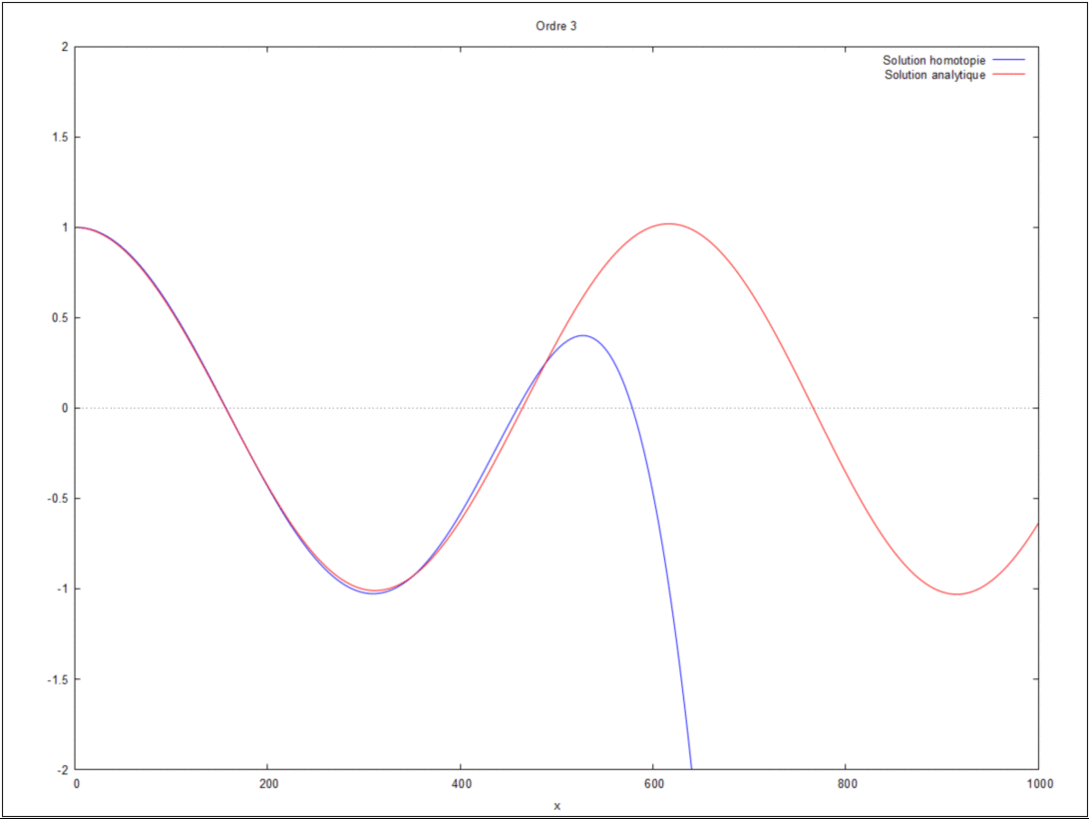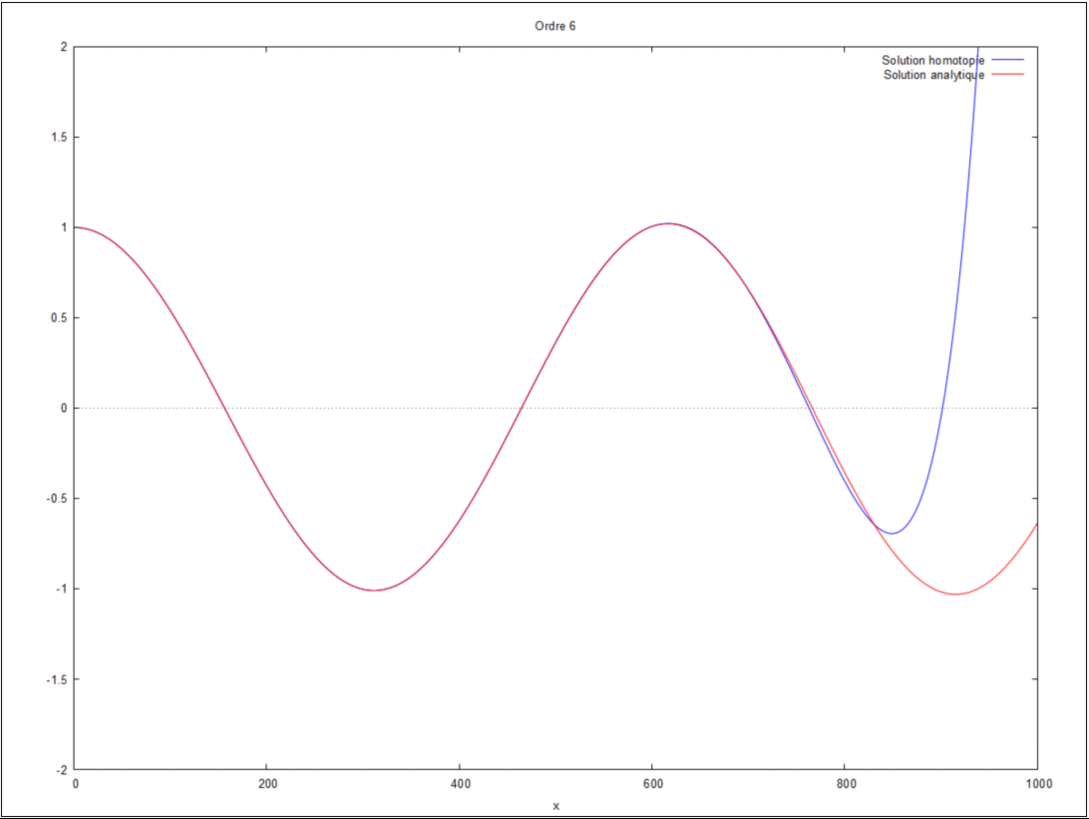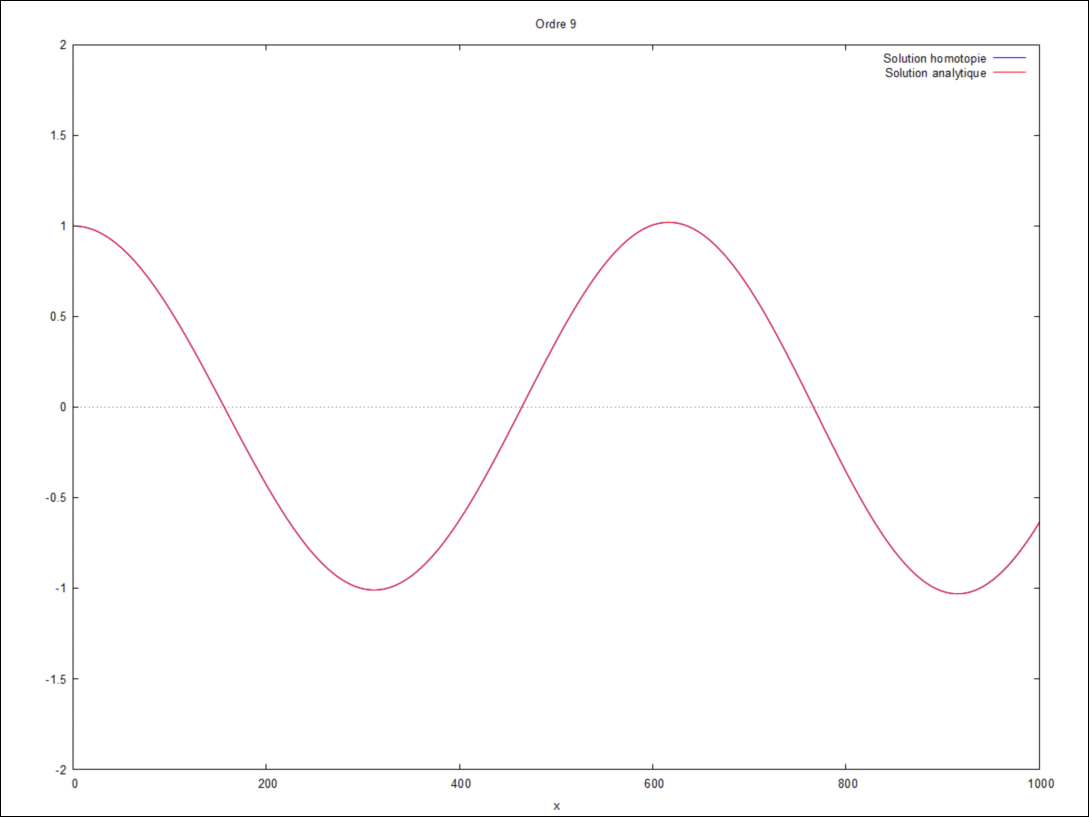
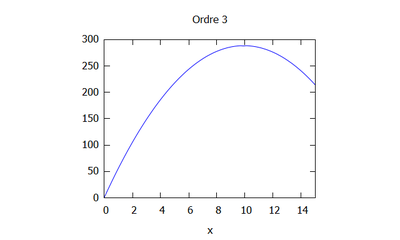
Ordres supérieurs

Pour les ordres supérieurs on effectue les calculs sur maxima jusqu'au rang n.

On peut ici voir la solution analytique comparée à la solution par homotopie selon son ordre ( de 0 à 10) :

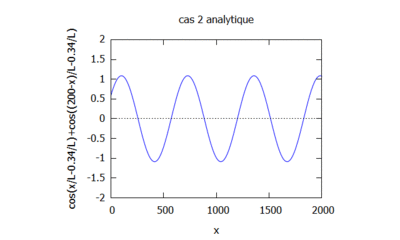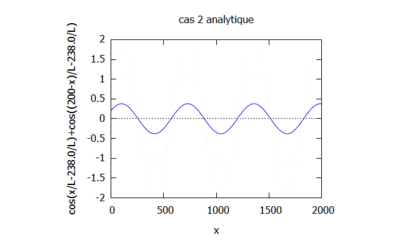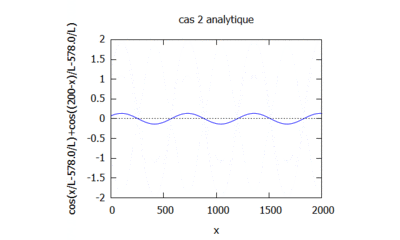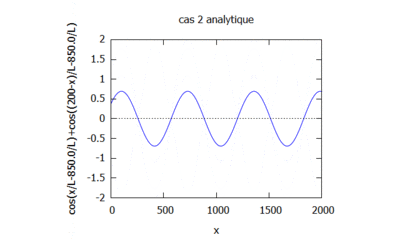
Cas n°2 : Canal monodimensionnel plat avec réflexion totale en amont

On étudie un canal uniforme unidimensionnel avec une réflexion totale en amont $ \partial\phi(x)/\partial x=0 $ et en aval une condition sur le flux $ \partial\phi/\partial x=ik(2-\phi) $. L'équation de Berkhoff est simplifiée de la même manière qu'avec le cas 1, seules les conditions aux limites changent. L'équation caractéristique : $ X^2+k^2=0 $ (similaire au cas 1)

Solution : $ A\exp(-ikx)+B\exp(ikx) $, A et B étant des constantes

On détermine A et B grâce aux conditions aux limites : A=$ \exp(2ikL) $ et B=1

Donc $ \phi(x)=\exp(ik(2L-x))+\exp(ikx) $

Ajouter une amplitude et une phase ne change pas cette solution. On peut alors écrire : $ \boxed{Φ(x,t)=\exp(i(k(2L-x)-wt)+\exp(i(kx-wt))} $

La hauteur d'eau est alors :

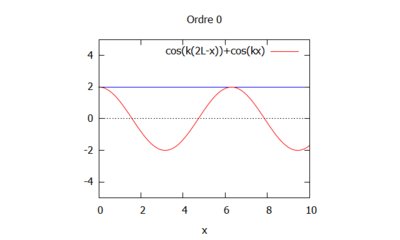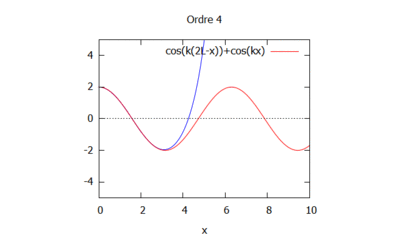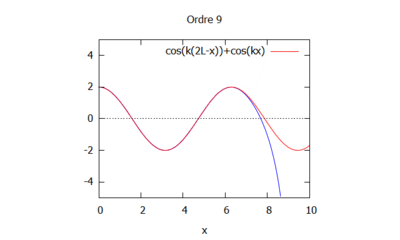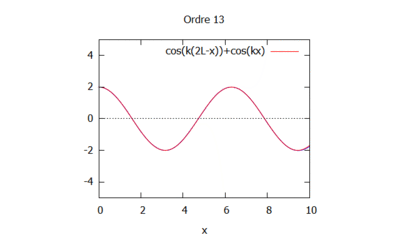
$ \boxed{h(x,t)=Re\phi(x,t)=\cos(k(2L-x)-wt)+\cos(kx-wt)} $

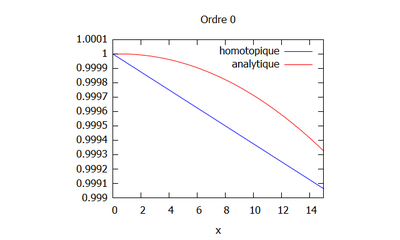
Solution analytique sur Maxima

Solution par homotopie

Ordre 0

On a $ \phi_0=Ax+B $

On détermine les constantes A et B grâce aux conditions aux limites :

en aval : $ x=L\to\partial\phi_0/\partial x =0\to A=0 $

en amont :$ x=0\to\partial\phi_0/\partial x =ik(2-\phi_0)=ik(2-Ax-B)=A \to ik(2-B)=0 \to B=2 $

Donc $ \phi_0=2 $

Ordre 1

On a $ \phi_1=-k^2\int\int\phi_0+A_1x+B_1 $

comme $ \int\int\phi_0=x^2 $, on a $ \phi_1(x)=-k^2x^2+A_1x+B_1 $

Grace aux conditions aux limites :

en aval $ x=L\to A_1=2k^2L $

en amont $ x=0\to\partial\phi/\partial x=\partial\phi_0/\partial x+p\partial\phi_1/\partial x=ik(2-\phi)\to B=2ikL $

Donc$ \phi_1(x)=-k^2x^2+2k^2Lx+2ikL $

Ordres supérieurs

On continue le processus sur n itérations. On peut ensuite calculer Re($ (\phi_0+....+\phi_n)\exp(-iwt) $)

Après calcul sur Maxima, avec les ordres de 0 à 13 :

On choisit k=1 et L=1/100 sinon l'homotopie ne fonctionne pas bien.

Analyse de la sensibilité de la solution

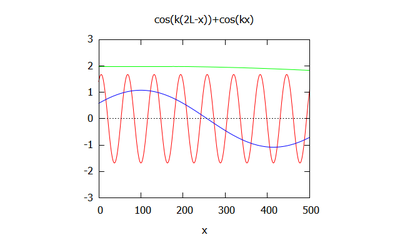
Si on fait varier le nombre d'onde en gardant kL constant on obtient:

Le nombre d'onde est ainsi modifié. Il induit la modification du cosinus et donc de la modélisation de la houle. En effet plus le nombre d'onde est élevé plus les vagues sont rapprochés.

Cas n°3 : Canal monodimensionnel avec fond de pente constante : sans onde réfléchie

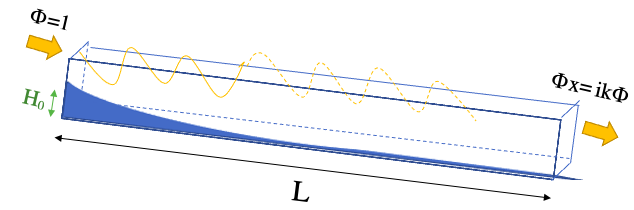
Domaine monodimensionnel de longueur L avec le fond du canal qui est en pente constante d'équation $ z = H_0 - sx $ avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $ et sortie libre amont $ \phi_x=ik\phi $.

On obtient après simplification de l'équation de Berkhoff : $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $.
avec $ H(x)=-αx+h $ tel que α représente la pente et h la profondeur d'eau à l'origine.

Résolution analytique

On cherche à mettre cette équation sous forme d'équation de Bessel de type : $ X^2*\phi_{xx} + X *\phi_{x} + X^2*\phi(x) = 0 $. En réalisant le changement de variable $ X = \frac{k*(H_0 - sx)}{P} $, on obtient la solution générale $ \boxed{Φ(x)=A.J_0(x)+B.Y_0(x)} $
avec $ J_0 $ une fonction de Bessel de 1ère espèce et $ Y_0 $ une fonction de Bessel de 2ème espèce.

D'après les conditions limites : $ \phi(0)=1 $ et $ \phi_x=ik\phi $. On trouve : $ \boxed{Φ(x)=\frac{J_0(x)*(ikY_0(L)-Y_1(L)) + Y_0(x)*(J_1(L)- ikJ_0(L))}{J_0(0)*( ikY_0(L) - Y_1(L))+Y_0(0)*(J_1(L)-ikJ_0(L))}} $

Résolution par la méthode d'homotopie

Ordre 0

On a donc la relation d'homotopie : $ (1-p)(\phi_{xx}-u_{0,xx})+p((h-αx)\phi_{xx}-α\phi_x(x)+k^2(h-αx)\phi(x))=0 $

$ \phi_{0,xx}=0 \Rightarrow \dfrac{\partial ϕ_0}{\partial x} = A \Rightarrow \phi_0=Ax+B $

On prend $ u_0=0 $ pour simplifier les calculs et les conditions limites suivantes : $ \phi(0)=1 $ et $ \phi_x=ik\phi $.

On obtiendra par le calcul: $ \boxed{Φ_0(x)=\dfrac{ikx}{1-ikL}+1} $

Ordre 1

conditions limites : $ \phi(0)=0 $ et $ \phi_x(x)=ik\phi $

$ \phi_{xx}=p*\phi_{1,xx}+\phi_{0,xx} $

De même, on obtient : $ \boxed{Φ_1(x)=-(-αx-1-h)\phi_0+α(\dfrac{ikx^2}{2(1-ikL)}+x)-k^2(\dfrac{ikx^3}{6(1-ikL)}+\dfrac{x^2}{2})+Ax+B} $

A et B calculés par la suite grâce aux conditions limites, alpha est la pente du canal

B=0

A=

Ordre 2

conditions limites : $ \phi_2^0=0 $ et $ \phi_{2,x}^L=ik\phi_{2}^L $

$ \phi_{2,xx}-\phi_{1,xx}+(H_0-sx)\phi_{1,xx}-s\phi_{1,x}+k^2(H_0-sx)\phi_1=0 $.

Ordre n

Résolution par récurrence,conditions aux limites : $ \phi_2^0=0 $ et $ \phi_{2,x}^L=ik\phi_{2}^L $.

$ \phi_{n,xx}-\phi_{n-1,xx}+(H_0-sx)\phi_{n-1,xx}-s\phi_{n-1,x}+k^2(H_0-sx)\phi_{n-1}=0 $.

Ordre 3

Ordre 4

Cas n°4 : Canal monodimensionnel avec fond de forme exponentielle et sortie libre en amont

Maintenant on s'intéresse à un canal monodimensionnel de largeur uniforme, de longueur L avec forme du fond exponentielle et sortie libre amont. On se place dans les conditions initiales suivantes : $ ϕ=1 $ et $ ϕ_x=ikϕ $
On pose $ H(x)=H_0e^{-sx} $

Résolution analytique

D'après le modèle de Berkhoff : $ ∇.(CCg∇ϕ)+k^2CCgϕ=0 $ et en remplaçant $ CCg = gH(x) $

On obtient : $ H(x)\phi_{xx}-H'(x)\phi_{x}+k^2H(x)\phi=0 $
soit, $ H_0\mathrm{e}^{-sx}\frac{\partial^2\phi}{\partial x^2}-sH_0\mathrm{e}^{-sx}\frac{\partial\phi}{\partial x}+k^2H_0\mathrm{e}^{-sx}\phi=0 $

En factorisant l'expression par $ H_0\mathrm{e}^{-sx}\neq0 $, on obtient une équation caractéristique du type : $ x^2-sx+k^2=0 $ avec $ x^2=\phi_{xx} $, $ x=ϕ_x $ et $ ϕ_0=1 $

On obtient donc 3 cas différents, selon le signe du discriminant : $ \Delta=s^2-4k^2 $

Si $ \color{Green}\Delta<0 $ : $ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[A\cos\Big(\frac{\sqrt{s^2-4k^2}}{2}x\Bigr)+B\sin\Big(\frac{\sqrt{s^2-4k^2}}{2}x\Bigr)] $

Si $ \color{Green}\Delta=0 $ : $ \phi(x)=(Ax+B)\mathrm{e}^{\frac{s}{2}x} $

Si $ \color{Green}\Delta>0 $ : $ \phi(x)=A\mathrm{e}^{\frac{s-\sqrt{s^2-4k^2}}{2}x}+B\mathrm{e}^{\frac{s+\sqrt{s^2-4k^2}}{2}x} $

Calcul des valeurs des constantes A et B grâce aux conditions limites $ \phi(0)=1 $ et $ \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(L) $ :

1er cas :

Si $ \color{Green}\Delta<0 $ : $ A=1 $ et en posant $ ρ=\frac{\sqrt{s^2-4k^2}}{2} $, $ B=\frac{ρ\sin(ρL)+\cos(ρL)(ik-s/2)}{ρ\cos(ρL)+\sin(ρL)(s/2-ik)} $

2ème cas :

Si $ \color{Green}\Delta=0 $ : $ B=1 $ et $ A=\frac{ik-\frac{s}{2}}{1-\frac{s}{2}L-ikL} $

3ème cas :

Si $ \color{Green}\Delta>0 $ : $ B=1-A $ et $ A=\frac{ik-\frac{s+\sqrt{s^2-4k^2}}{2}}{ik-\frac{s+\sqrt{s^2-4k^2}}{2}+ik-\frac{-\sqrt{s^2-4k^2}+ik}{2}} $

Résolution par la méthode d'homotopie

On résout par la méthode homotopie l'équation suivante : $ (1-p)\phi_{xx} + p(\phi_{xx}-s\phi_{x}+k^2\phi)=0 $
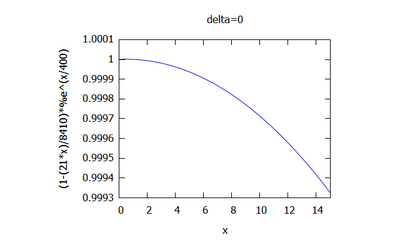
On prend $ s=1/200 $, $ k=1/400 $ et $ L=10 $

Ordre 0

On résout : $ \phi_0=Ax+B $.

Avec les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, on obtient :

$ \boxed{\phi_0=1+\dfrac{ik}{1-ikL}x} $

Ordre 1

Conditions aux limites :$ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $.

On résout : $ \phi_{xx,1}-s\phi_{x,0}+k^2\phi_{0}=0 $

On trouve $ \phi_1=s\dfrac{ik}{1-ikL}\dfrac{x^2}{2}-k^2\dfrac{x^2}{2}+\dfrac{k^3 i}{1-ikL}\dfrac{x^3}{6}+Ax+B $

Avec $ A=\dfrac{ik\Big(\dfrac{sik}{1-ikL}\dfrac{x^2}{2}-k^2\dfrac{x^2}{2}-\dfrac{k^3 i}{1-ikL}\dfrac{x^3}{6}\Big)-\dfrac{sik}{1-ikL}x+k^2 x+\dfrac{k^3 i}{1-ikL}\dfrac{x^2}{2}}{1-ikx} $

et $ B=0 $

Ordre 2

Conditions aux limites : $ \phi_2^0=0 $ et $ \phi_{2,x}^L=ik\phi_{2}^L $.

On résout : $ \phi_{xx,2}-s\phi_{x,1}+k^2\phi_{1}=0 $

Ordre n

On résout : $ \phi_{xx,n}-s\phi_{x,n-1}+k^2\phi_{n-1}=0 $

Analyse des résultats, limites et intérêt de la méthode d'homotopie

Intérêts de la méthode d'homotopie

La méthode d'homotopie comme nous venons de l'illustrer peut permettre la modélisation des ondes, en l'occurence ici, de la houle qui est un phénomène complexe. En effet on peut a l'aide de cette méthode modéliser les réflexions, réfraction ou diffraction des ondes aquatiques. Une solution mathématique simple converge par la méthode d'homotopie vers une solution finale complète. Le paramètre p variant de 0 a 1 permet d'approcher la solution recherchée.

Ceci nous permet de mieux comprendre le comportement de cette houle sur nos cotes (prévision de submersions marines ou d'érosion).

Limites des résultats obtenus

Cependant, il existe des limites à ce modèle,on peut dire que l'homotopie ne marche pas toujours en fonction de la valeur de k .

Paramètres naturels et physiques

Tectonique des plaques, séismes, transport sédimentaire influençant le fond du canal (hypothèse de fond plat), tous ces paramètres naturels difficilement quantifiables et aléatoires ne permettent pas au modèle de coller parfaitement à la réalité.

De plus les phénomènes de réfraction et diffraction sont plus importants dans la réalité car le trait de côte ne se limite pas à un parfait trait horizontal comme précisé dans le modèle.

Approximation mathématique

En effet, la houle est considérée constante or un phénomène naturel de cette ampleur n'est pas réellement constant.

De plus les constantes L et k sont des approximations mathématiques de phénomènes naturels, par définition le modèle s'éloigne de la réalité au fur et à mesure qu'on le simplifie mathématiquement.