Wikibardig:Étude micromécanique de la transition des régimes hydriques dans les sols granulaires partiellement saturés

Présentation issue de la thèse de Nabil Younes - 2023. École doctorale Euclide de la Rochelle en partenariat avec University of Calgary.

Téléchargez le document ici

Contexte général

Depuis la révolution industrielle, la Terre subit des changements climatiques majeurs, se traduisant par une montée du niveau de la mer, ce qui engendre un risque crucial pour les communautés côtières. Afin d'éviter les catastrophes d'inondation, les êtres humains ont eu une idée de génie de construire ce que l'on appelle aujourd'hui : les digues.

Les digues en remblai sont généralement construites à partir de matériaux granulaires compactés et se trouvent souvent dans des conditions de saturation partielle, ce qui confère à leurs matériaux une certaine cohésion bénéfique pour leur résistance mécanique dite cohésion capillaire. Cependant, lorsque ces matériaux granulaires, situés à la surface de la digue, sont exposés à des cycles de séchage et de mouillage, typiquement provoqués par la variation de pression entre l'amont et l'aval de la digue, ils peuvent devenir vulnérables et risquent de s'effondrer.

On peut ainsi considérer l'eau comme une arme à double tranchant : en quantité modérée dans le sol, elle favorise sa cohésion, mais en cas d'absence ou d'excès, la cohésion capillaire disparaît. Ces fluctuations sont généralement engendrées par plusieurs facteurs, tels que des précipitations intenses, des vagues de chaleur, les marées ou encore les tempêtes, des phénomènes malheureusement de plus en plus fréquents dans un contexte de changement climatique.

Aujourd'hui, il est admis que les instabilités des digues au niveau macroscopique sont dues à des instabilités microscopiques [1]. Avant d'étudier ces instabilités microscopiques, il est indispensable de comprendre, dans un premier temps, la physique et la mécanique des milieux partiellement saturés, ainsi que l'impact crucial des fluctuations de la teneur en eau sur la cohésion capillaire de ces sols. La présente thèse s'inscrit dans le cadre du projet StabDigue, financé pour une durée de cinq ans par la région Nouvelle-Aquitaine, pour l'étude de la stabilité des digues en remblai partiellement saturées. Cette thèse de doctorat est motivée par plusieurs questions clés qui seront abordées :

• Peut-on modéliser et prédire les conséquences sur la stabilité mécanique des sols granulaires dues au changement la teneur en eau ?
• Comment les cycles de mouillage/séchage vont-ils affecter les propriétés hydromécaniques des sols granulaires ?
• Est-il possible d'interpréter ces changements hydromécaniques en terme de microstructure sous-jacente ?

Les lacunes dans la littérature, motivations de cette étude et objectifs

La problématique centrale réside dans le fait que la physique des sols partiellement saturés se situe à l'échelle des pores et des grains solides, ce qui requiert une étude microstructurale pour analyser les interactions entre les phases solide-liquide-gaz et leur impact sur le comportement global d'un sol partiellement saturé. La grande majorité des études, qu'elles soient expérimentales, analytiques ou numériques, dans la littérature, se sont focalisées sur les configurations se trouvant dans le régime pendulaire [2]–[9]. Aujourd'hui, le régime pendulaire est bien compris par les géomécaniciens et les chercheurs. Cependant, ce régime ne représente qu'une petite portion des sols non-saturés. Ces derniers se trouvent généralement dans les régimes funiculaire et capillaire. Hélas, la plupart des études dans la littérature ont été consacrées uniquement au régime pendulaire. Lorsque le régime funiculaire est étudié pour les triplets, les chercheurs se sont contentés d'utiliser des critères géométriques, souvent analytiques, afin de modéliser la coalescence ou la rupture des ponts capillaires [10], [11]. Ces critères géométriques, aussi pratiques soient-ils, rendent la modélisation des milliers de particules en régime funiculaire et capillaire quasi-impossible.

Pour s'affranchir de ces approximations et pour modéliser des milieux granulaires partiellement saturés pour tous les régimes possibles, nous proposons un couplage entre la méthode aux éléments discrets dite DEM pour simuler le squelette solide en forme de particules sphériques et la méthode de Boltzmann sur réseau dite LBM afin de modéliser les ponts capillaires eau-air entre les particules solides. Concernant la LBM, un code maison a été développé sur des cartes GPU (Graphical Processing Units) qui est basé sur la résolution des équations Navier-Stokes et Allen-Cahn afin de prendre en compte l'interface eau-air des ponts capillaires. En ce qui concerne la DEM, le logiciel à accès libre YADE a été utilisé [12].

Validation numérique et résultats

Avant de s’attaquer à l’étude du matériau en considérant un volume élémentaire représentatif (VER), plusieurs benchmarks et validations ont été nécessaires pour le modèle LBM, notamment en ce qui concerne la prédiction précise de la forme des ponts capillaires ainsi que les forces associées. A l’équilibre mécanique de la simulation LBM, les formes des ponts capillaires entre deux grains solides sphériques coïncident parfaitement avec la solution théorique de l’équation de Young-Laplace. De plus, les résultats trouvés par la LBM montrent qu’elle est capable de retrouver l’inversion de signe de la courbure moyenne H quand la distance de séparation entre les deux particules augmente. En outre, une nouvelle expression numérique pour le calcul des forces capillaires entre des grains sphériques a été proposée. Cette nouvelle formulation a montré ses capacités à calculer de façon assez précise les forces capillaires résultant des ponts capillaires isolés et coalescents entre deux et trois particules sphériques, en les comparant avec des résultats expérimentaux et numériques dans la littérature. L’avantage de l’approche LBM est sa capacité à modéliser la fusion des ponts capillaires de façon intrinsèques sans avoir besoin de passer par des critères de fusion géométrique. Ainsi, ces résultats montrent que la LBM est capable de modéliser le passage du régime pendulaire au régime funiculaire.

Ensuite, le couplage DEM-LBM est mis en place pour explorer les caractéristiques des assemblages granulaires partiellement saturés pour tous les régimes capillaires. Nous avons pu retrouver la forme classique de la courbe de rétention qui est définie par l’évolution de la succion en fonction du degré de saturation. De plus, l’évolution de la contrainte capillaire moyenne, qui pourrait être considérée comme étant la cohésion apparente, a été tracée en fonction du degré de saturation. Nous observons une augmentation de la contrainte capillaire moyenne avec l’augmentation du degré de saturation jusqu’à un certain seuil au-delà duquel la contrainte capillaire moyenne diminue pour atteindre zéro lorsque le système devient complètement saturé. Par ailleurs, nous avons également démontré que le paramètre de Bishop pour les contraintes effectives n’est jamais égal au degré de saturation. Ces derniers résultats ont été comparés avec des données numériques déjà existantes dans la littérature.

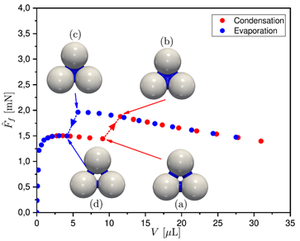
Nous avons enfin exploité la pleine capacité du couplage DEM-LBM pour simuler des cycles de séchage (évaporation) et de mouillage (condensation) dans les sols non-saturés. Cela a été réalisé à la fois sur de petits assemblages granulaires composés de trois et quatre particules sphériques, ainsi que sur des VER constitués de quelques milliers de grains. Tout d'abord, pour les trois particules sphériques, nous avons réussi à reproduire avec succès les sauts (chutes) des forces capillaires, estimées à 30% au moment de la coalescence (rupture) des ponts capillaires. Ceci est démontré dans le cas des trois particules sphériques, tel qu'illustré sur la Figure (1) et nous avons ensuite comparé ces résultats avec des études expérimentales et théoriques [13], [14]. Un autre résultat assez remarquable est que nous avons constaté que, pour une même configuration et un même angle de mouillage, le volume auquel les ponts se fusionnent est différent de celui auquel les ponts se rompent, phénomène appelé l'hystérésis. En effet, nous avons observé que lors de la coalescence, la fusion n'aura lieu que si les interfaces capillaires se touchent. En revanche, la rupture des ponts capillaires se produit quand l'épaisseur du pont, dans le plan passant par les centres des particules sphériques, devient nulle.

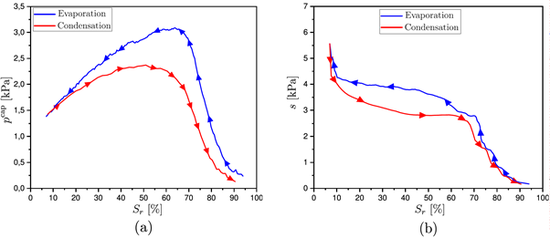
A l'échelle du VER, nous avons mis en évidence que la succion et la contrainte moyenne sont plus élevées lors de l’évaporation que celles qui ont été observées lors la condensation pour le même angle de mouillage comme le montre la Figure 2. Nous avons également montré que la contrainte capillaire moyenne (cohésion apparente) devient nulle quand le système devient complètement sec ou saturé, comme observé précédemment.

Figure 1 : L'évolution de la force capillaire Ff [mN] en fonction du volume d'eau [μL]

Figure 2 : Les évolutions (a) de la contrainte capillaire moyenne p^cap [kPa] et (b) de la succion s [kPa] en fonction du degré de saturation Sr [%]

Conclusion et perspectives

Pour rappel, l'étude bibliographique effectuée dans ce mémoire a mis en évidence d'importantes lacunes dans la compréhension des milieux granulaires partiellement saturés, notamment le fait que la plupart des études se sont concentrées uniquement sur le régime pendulaire. Par conséquent, l'objectif principal de cette thèse était de développer un modèle numérique capable de simuler les matériaux granulaires partiellement saturés pour tous les régimes possibles : pendulaire, funiculaire et capillaire. Cela a justifié le choix d'utiliser le modèle DEM-LBM, capable de modéliser facilement cette transition entre les régimes, pour étudier et exploiter les milieux granulaires partiellement saturés.

Les perspectives de ces travaux sont nombreuses et peuvent-être résumés en quelques points :

4.1 Existence d'une contrainte effective

L'existence de la contrainte effective est depuis longtemps un problème ouvert et majeur pour les géomécaniciens à la fois sur le niveau numérique et expérimental. L'existence de la contrainte effective n'a été justifiée que dans le régime pendulaire lors de la rupture de l'échantillon, c-à-d à la limite plastique. Cependant, la réponse reste malheureusement en suspens pour les régimes funiculaire et capillaire. C'est là où le couplage DEM-LBM entre en jeu afin d'étudier plus en détail cette question dans tous les régimes possibles.

4.2 Instabilités à l'échelle du VER

Dans le cadre du projet StabDigue, l'étude la plus cruciale concerne la détermination quantitative des instabilités des sols granulaires partiellement saturés soumis à des cycles de mouillage/séchage. Cet aspect peut être abordé en utilisant le soi-disant critère du travail du second ordre W^2 [1], capable de décrire de manière précise l'effondrement des sols granulaires secs. En utilisant le couplage DEM-LBM ainsi que les expressions analytiques récemment dérivées par [15], nous avons l'opportunité de calculer de façon précise le W^2 pour tous les régimes possibles.

4.3 Couplage avec des approches macroscopiques

La modélisation des digues en utilisant le couplage DEM-LBM avec des millions de particules, semble impossible et irréalisable en raison du calcul très intensif. Pour surmonter ce problème, il est envisageable d'intégrer le modèle DEM-LBM avec une méthode macroscopique telle que la méthode des éléments finis (FEM), la méthode des différences finies (FDM) ou la méthode du point matériel (MPM). Actuellement, en parallèle de ma thèse, des chercheurs à l'Université de La Rochelle explorent la possibilité d'utiliser le DEM-LBM comme une loi de comportement pour modéliser, à l'échelle réelle, les digues en remblai.

Pour conclure, le couplage DEM-LBM a montré ses capacités à analyser finement, la physique des matériaux granulaires partiellement saturés à l'échelle macroscopique, et plus particulièrement les transitions fluides entre les régimes capillaires. Ce modèle numérique nous permis de comprendre des aspects qui pourraient sinon rester inaccessibles dans des expériences de laboratoire. Nous pourrons avec ce fameux modèle de repousser les limites de notre compréhension des sols partiellement saturés. Nous pourrons également proposer des solutions aux paradoxes actuelles et contribuer au développement de la géomécanique dans son entièreté.

Références

[1] R. Wan, F. Nicot, and F. Darve, Failure in geomaterials: a contemporary treatise. Oxford: Elsevier, 2017.

[2] L. Scholtes, “Modélisation micromécanique des milieux granulaires partiellement saturés,” PhD thesis, Institut National Polytechnique de Grenoble-INPG, 2008.

[3] L. Scholtès, B. Chareyre, F. Nicot, and F. Darve, “Micromechanics of granular materials with capillary effects,” International Journal of Engineering Science, vol. 47, no. 1, pp. 64–75, Jan. 2009, doi: 10.1016/j.ijengsci.2008.07.002.

[4] L. Scholtès, P. ‐Y. Hicher, F. Nicot, B. Chareyre, and F. Darve, “On the capillary stress tensor in wet granular materials,” Num Anal Meth Geomechanics, vol. 33, no. 10, pp. 1289–1313, Jul. 2009, doi: 10.1002/nag.767.

[5] J. Duriez and R. Wan, “Stress in Wet Granular Media with Interfaces via Homogenization and Discrete Element Approaches,” J. Eng. Mech., vol. 142, no. 12, p. 04016099, Dec. 2016, doi: 10.1061/(ASCE)EM.1943-7889.0001163.

[6] J. Duriez and R. Wan, “Contact angle mechanical influence in wet granular soils,” Acta Geotech., vol. 12, no. 1, pp. 67–83, Feb. 2017, doi: 10.1007/s11440-016-0500-6. [7] J. Duriez, M. Eghbalian, R. Wan, and F. Darve, “The micromechanical nature of stresses in triphasic granular media with interfaces,” Journal of the Mechanics and Physics of Solids, vol. 99, pp. 495–511, Feb. 2017, doi: 10.1016/j.jmps.2016.10.011.

[8] J. Duriez and R. Wan, “A micromechanical μ UNSAT effective stress expression for stress-strain behaviour of wet granular materials,” Geomechanics for Energy and the Environment, vol. 15, pp. 10–18, Sep. 2018, doi: 10.1016/j.gete.2017.12.003.

[9] B. Mielniczuk, O. Millet, G. Gagneux, and M. S. El Youssoufi, “Characterisation of pendular capillary bridges derived from experimental data using inverse problem method,” Granular Matter, vol. 20, no. 1, p. 14, Feb. 2018, doi: 10.1007/s10035-017-0784-8.

[10] M. Miot, G. Veylon, A. Wautier, P. Philippe, F. Nicot, and F. Jamin, “Numerical analysis of capillary bridges and coalescence in a triplet of spheres,” Granular Matter, vol. 23, no. 3, p. 65, Aug. 2021, doi: 10.1007/s10035-021-01127-0.

[11] F. Z. E. Korchi, “Approche expérimentale multi-échelle de l’effondrement capillaire de sols granulaires,” Université de Montpellier, 2017.

[12] V. Smilauer et al., “Yade Documentation,” 2023, doi: 10.48550/ARXIV.2301.00611.

[13] J.-P. Gras, “Approche micromécanique de la capillarité dans les milieux granulaires: rétention d’eau et comportement mécanique,” PhD thesis, Université de Montpellier II-Sciences et Techniques du Languedoc, 2011.

[14] G. Gagneux and O. Millet, “An analytical framework for evaluating the cohesion effects of coalescence between capillary bridges,” Granular Matter, vol. 18, no. 2, p. 16, May 2016, doi: 10.1007/s10035-016-0613-5.

[15] M. Eghbalian, M. Pouragha, and R. Wan, “Micromechanical formulation of first‐ and second‐order works in unsaturated granular media,” Num Anal Meth Geomechanics, vol. 47, no. 7, pp. 1152–1174, May 2023, doi: 10.1002/nag.3509.