ANSWER - Plage de Biarritz, France
Ces vidéos font parties des réalisations produites dans le cadre de l'Opération ANSWER. Cette dernière a pour objectif de faire collaborer le public et les scientifiques autour des sciences de l'eau afin d'améliorer les connaissances dans le domaine.
Sommaire |
Le défi
| Plage de Biarritz, France | La vidéo de David G., Paris
VIDEO QUESTION La plage de Biarritz est le siège d'un phénomène bien singulier !. |
| Plage de Biarritz, France | La vidéo de David G., Paris
VIDEO REPONSE La plage de Biarritz est le siège d'un phénomène bien singulier ! Retrouvez le détails de l'explication scientifique ci-dessous! |
Les propositions du public
- La proposition de Guillaume :
« C’est un phénomène que j’ai déjà observé sur d’autres plages d’Aquitaine. Selon moi il s’agit de deux ondes quasi parallèles qui se télescopent (soit une vague et un reflux, soit deux vagues allant à des vitesses différentes) ce qui crée des éclaboussures. On a l’impression que quelque chose se propage en parallèle à la plage, mais ce n’est qu’une illusion d’optique car les ondes sont presque parallèles. »
- La proposition de Dominique :
« Il peut s’agir d’un déferlement avec un "peel angle" (angle de déferlement) très faible qui dépend de l'incidence de la vague et de la bathymétrie du fond. S’il y a un léger décalage entre les isobathes et les isophases de la houle, l’angle de déferlement est non nul et le pont de déferlement se déplace alors le long de la plage. Ce déplacement peut être très rapide si l'écart angulaire est très faible. »
- La proposition de Nejema :
« Le bord de l'eau semble légèrement plus profond que l’endroit où se trouve les baigneurs, tel un "bassin de baïne" (bâche, sillon de plage). Les vagues semblent apporter de l'eau dans ce bassin de baïne. Cette même eau a tendance à retourner (par des courants de fonds) vers le large pour maintenir un équilibre. Lorsque celle-ci se dirige vers le large et rencontre une vague se propageant dans le sens inverse, il y a couplage de leurs énergies. On pourrait assimiler ce phénomène à de mini vagues scélérates. »
- La proposition de Déborah :
« J’ai déjà observé ce phénomène dans divers environnements tels que la Bretagne ou le Sri Lanka. Je pense qu’il s’agit de la collision entre les vagues incidentes (venant du large) et les vagues réfléchies à la côte. Sur le film de Biarritz, on le devine par exemple au temps 00:42. »
- La proposition de Ywenn :
« Le phénomène observé à Biarritz est classique et bien connu des surfers car cela gêne sa pratique. Il s’agit de la rencontre d’un "backwash" avec une vague. Lorsque la pente de la plage est très forte, l’onde des vagues est réfléchie vers le large et vient donc à l’encontre des autres vagues ; ce qui peut donner ce type de "déferlement" ou "jaillissement" suivant la rythmicité des séries de vagues. »
- La proposition de Jacques:
« Je suppose que le phénomène est la "flèche" qui se produit à l'intersection de la vague montante et de la vague retour causée par un ressaut de la plage non parallèle au train de vagues montantes. »
- La proposition de Pierre-Olivier:
« Il se trouve que la vague casse (déferle) à l’approche d’une remontée du fond. Si la vague arrive selon une ligne de front parallèle à la côte, le déferlement intervient en même temps sur tout le front de la vague. Si la vague arrive avec un angle alfa par rapport à la ligne de côte, alors la vague déferlera d’abord sur la partie en avance et progressivement vers la partie en retard. Cela donne une impression de mouvement d’un coté à l’autre de la vague, alors qu’il n’y a ni transfert de masse, ni même transfert d’information. Ce mouvement est d’autant plus rapide que alfa est petit, avec une vitesse tendant vers +Infini quand alfa tend vers 0 (déferlement instantané sur toute la ligne de vague).»
- La proposition de Jérôme:
« La vitesse qu'on observe n'est pas celle de particules fluides mais la vitesse de propagation du "point" de déferlement le long du rivage. Dans le cas de la vidéo, la vague doit arriver presque parallèlement au rivage qui doit avoir une morphologie presque constante le long de la zone observée. »
- La proposition de Serge:
« Il s'agit d'une interférence entre les ondes (vagues) arrivant du large et les ondes réfléchies par le littoral, qui dans ce cas précis ne sont pas réfléchies parfaitement perpendiculairement à la plage. Il semblerait que l'onde arrive avec une petite incidence. »
- La proposition de Jean-Benoit:
« Il s’agit très probablement d’un retour de vague créé par une cuvette dans le sable (très présentes à Biarritz). Ce retour ayant subi une accélération due à la pente montante, il crée un soulèvement de l’eau lors de sa rencontre avec la vague suivante. Le parcours rapide sur la plage peut même être instantané dans de rares cas si les deux vagues sont parfaitement parallèles lors de leur rencontre. On peut également observer ce phénomène lorsque des digues renvoient les vagues vers la mer. »
- La proposition de Stéphane:
« Il s'agit d'un phénomène lié aux vagues réfléchies par la plage. Cette dernière peut interagir avec l'onde incidente qui dans cette zone est proche du déferlement. Cela crée une instabilité de crête qui projette l'eau vers le haut. L'impression de déplacement latéral de l'instabilité vient d'un effet géométrique. Si l'angle alpha des ondes incidentes est faible, l'onde réfléchie aura un angle -alpha également faible. Les ondes incidentes et réfléchies se déplaçant à des célérités opposées, le point d'intersection se déplace alors latéralement à très grande vitesse.»
- La proposition de Louis-Joseph:
« Pas compliqué! Il s’agit d’une vague réfléchie qui rencontre (avec un léger angle) la vague incidente suivante. On observe la crête d’addition des deux vagues qui donne l’apparence de se déplacer alors qu’en fait aucune molécule d’eau ne bouge horizontalement si vite. »
Les explications du « phénomène étrange » constaté sur la plage de Biarritz
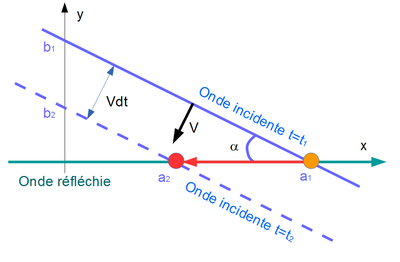
Comme on peut le constater sur la « vidéo réponse », ce phénomène correspond à la rencontre de deux ondes : une onde incidente (en bleu sur le diagramme) et une onde réfléchie par le haut de plage. Ces deux vagues se croisent avec un angle a au point « rouge » à droite. Ainsi, à droite du point orange, on peut voir une ligne de déferlement continu et à gauche rien puisque les vagues ne se sont pas encore croisées.
Le phénomène apparent qui semble correspondre à une « onde » se déplaçant à très grande vitesse est en fait un artefact. Il correspond en fait à une « impression visuelle » qui ne correspond à aucun mouvement transversal.
Essayons d’expliquer et de quantifier ce phénomène en nous basant sur le diagramme suivant:
Nous avons à l’instant $ t=t_1 $ d’un côté une onde incidente en bleu continu et de l’autre une onde réfléchie en vert continu.
Nous allons choisir un repère lié à l’onde réfléchie. Nous voyons l’onde incidente se rapprocher de l’onde réfléchie à une vitesse $ V $ (égale en fait à la somme des vitesses des 2 ondes : $ V=V_\text{reflechie} + V_\text{incidente} $ qui peuvent être différentes). L’intersection des 2 ondes en trait continu est représentée par un point orange situé à l’abscisse $ a_1 $ qui correspond à un point de déferlement.
A l’instant suivant $ t_2 $ l’onde incidente (en bleu pointillé) s’est rapprochée de l’onde réfléchie d’une quantité $ Vdt $ (où $ dt=t_2-t_1 $) et ce que l’on voit depuis la plage, c’est le déplacement du point orange vers le point rouge qui est maintenant à l’abscisse $ a_2 $. De même que précédemment, à droite du point rouge, on peut voir une ligne de déferlement continu et à gauche rien puisque les vagues ne se sont pas encore croisées.
Essayons maintenant de calculer la vitesse de ce point rouge.
Nous avons : $ \sin\alpha=Vdt/da $ d’où la vitesse du point rouge : $ V_a=da/dt=V/\sin\alpha $
Ainsi,plus l’angle a est petit, plus $ V_a $ est grand
Le graphique suivant représente la fonction précédente pour 2 valeurs de $ V $ : $ V $=2m/s et pour $ V $=1m/s. Ainsi, $ V_a $ augmente considérablement lorsque l’angle d’incidence diminue. On pourrait enregistrer des vitesses apparentes du phénomène de l’ordre de 400 km/h pour une vitesse $ V $ de 2 m/s et pour un angle de croisement de 1 degré. Cette vitesse diminue de moitié pour un angle de 1m/s.
Nous vérifions enfin que pour un angle de 90°, la vitesse apparente est bien la vitesse et que pour un angle de 0°, la vitesse $ V $ est infinie (toute la ligne déferle en même temps), ce que l’on observe dans la plupart des cas : le déferlement sur une ligne est "instantané".
Conclusion
- ne nous fions donc pas à une première impression visuelle !
- pour mesurer précisément l’angle de réflexion d’une plage, nous pourrions mesurer la vitesse apparente de ce phénomène, connaissant la vitesse d’incidence des houles (il faut alors se placer dans des conditions de marée et de houles particulières)
Revenir à la liste des contributions!
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS