ANSWER : Hydrogramme sur un plan incliné
Sommaire |
Eléments de contexte
Cette page fait partie de la démarche collaborative ANSWER , dont l'objectif est de faire collaborer scientifiques et grand public autour du domaine de l'eau.
Le diagramme suivant illustre le positionnement de la page dans la partie de ANSWER consacrée à la morphodynamique.
Chaque "perle" représente une solution analytique (perle "cliquable" sur le diagramme ci-dessous) qui renvoie sur une page plus théorique.
Introduction
L'objet principal de l'hydrologie quantitative est d'étudier la genèse et le propagation des écoulements sur les bassins versants soumis à des averses de pluie. Ces précipitations peuvent être à l'origine d'inondations importantes et produire des dégâts matériels, voire la perte de vies humaines.
L'importance de ces évènements est fonction de l'intensité et de la distribution spatiale de la pluie, mais également des caractéristiques des bassins versants: topographie, nature des sols, état de la végétation... En particulier, la capacité d'absorption des sols en eau est un facteur limitant du volume ruisselé.
Pour étudier ces processus, le recours à la modélisation est donc de première importance. Nous nous placerons ici dans le cas très schématique d'une surface imperméable, ce qui signifie qu'il n'y a aucune infiltration et que toute l'eau de pluie ruisselle et s'écoule vers l'exutoire du bassin versant.
Observation en nature
Des photos ou des vidéos enregistrées en nature peuvent donner une vision dynamique et réaliste du phénomène de modification des fonds.
Essais en laboratoire
Des essais en laboratoire peuvent être envisagés pour reproduire partiellement ces deux phénomènes. En effet, ces derniers ne peuvent être obtenus de manière très pure, car la turbulence de l'écoulement induit des phénomènes qui ne sont pas pris en compte dans les deux cas traités ci-dessus.
Systèmes d'équations
Nous faisons un certain nombre d'hypothèses à partir des équations de Navier-Stokes afin d'obtenir un modèle plus simple.\\
- fluide incompressible
- domaine monodimentionnel infini
- intégration dans la verticale
- pente constante
- accélération verticale négligeable
- frottement négligeable
L'équation simplifiée résultante est une équation de type "onde cinématique" qui s'écrit:
$ (1)\quad \frac{\partial h }{\partial t}+\frac{\partial q }{\partial x}=i $
où h(m) est la hauteur d'eau sur le plan incliné, $ q(m^2/s/ml) $ le débit liquide, $ i(m/s) $ l'intensité de la pluie.
Le débit peut être exprimé par une formule empirique du type:
$ (2)\quad q(x,t)=\alpha h(x,t)^{\beta+1} $
qui peut être de type Manning-Strickler :
$ (3)\quad q=\frac{1}{n}h^{5/3}p^{1/2} $
où $ p $ est la pente locale du domaine. Si nous injectons (2) dans (1), il vient:
$ (4)\quad \frac{\partial h }{\partial t}+\alpha (\beta+1) h^\beta \frac{\partial h }{\partial x}=i $
qui est l'équation à résoudre.
Cas test étudié
Nous choisissons de traiter l'évolution du film d'eau qui se crée lorsqu'une pluie d'intensité constante $ i=100 mm/h $ tombe sur une surface de longueur $ L=100m $, de pente $ p=10\% $ et de coefficient de rugosité de Manning égal à $ n=0,1m^{1/3}.s $. Nous étudierons l'évolution de la lame d'eau pendant 1 heure.
Sur le plan qualitatif, la pluie qui tombe de manière uniforme sur l'ensemble du plan incliné va produire une accumulation d'eau en tout point du domaine et provoquer un écoulement vers l'aval. Le domaine va donc se charger d'une lame d'eau qui va s'épaissir vers l'aval. Ce régime, s'il dure suffisamment longtemps va devenir permanent, c'est-à-dire que le débit qui sort par l'exutoire du domaine (section aval) va équilibrer exactement le débit de pluie qui tombe sur le domaine. Ce débit qui sort en régime permanent à l'aval du domaine a pour expression: $ Q=Li=10m^3/ml/h $
Ce régime va ensuite se maintenir tant que tombe la pluie. Lorsque la pluie cesse (ici au bout de 1200 s), le domaine va se vidanger progressivement par l'aval. Nous pouvons donc considérer 3 intervalles de temps:
- la mise en charge du domaine jusqu'à obtention du régime permanent, qui s'établit lorsque la première goutte tombée sur la section amont du domaine se retrouve au droit de la section aval t=0 à t=te
- le temps du régime permanent t=te à t=1200s
- la vidange du domaine à partir de l'arrêt de la pluie t=1200s à t=3600s
Résolution de l'équation d'onde cinématique
Il s'agit d'une équation non-linéaire de convection pure (onde cinématique) que nous pouvons résoudre par la méthode des caractéristiques.
Nous pouvons en effet écrire:
$ (5)\quad \frac{d h }{d t} = \frac{\partial h }{\partial t} +\frac{dx }{d t} \frac{\partial h }{\partial x}=i $
Nous obtenons alors le système suivant en comparant avec (4):
$ (6)\quad\begin{cases} \frac{d h }{d t}=i \\ \frac{d x }{d t}= \alpha (\beta+1) h^\beta \end{cases} $
Avec $ \alpha=\sqrt{p}/n \simeq 3.16 $ et $ \beta=2/3 $
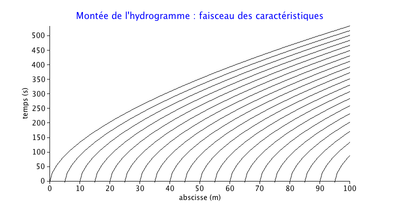
Montée de l'hydrogramme
Ainsi, nous avons $ h=it $ (en intégrant (6)) le long de la caractéristique d'équation:
$ (7)\quad \frac{d x }{d t} = \alpha (\beta+1) {it}^{\beta} $
Ce qui conduit après intégration entre le pied de la caractéristique au temps $ t=0 $ et l'abscisse du point $ x $ (calculé au temps $ t $).
$ (8)\quad x=x_A+\frac{ \alpha}{i} (it)^{\beta+1} $
Le faisceau des caractéristiques est représenté sur la figure 1.
Nous allons supposer que la durée de la pluie est suffisamment longue pour produire sur tout le domaine un régime permanent ($ t_e $).
Ce régime permanent apparaît lorsque la première goutte de pluie qui tombe sur l'extrémité amont du domaine ($ x=0 $) atteint l'extrémité aval de l'exutoire (en $ x=L $).
Autrement dit, lorsque la caractéristique qui part de l'abscisse $ x=0 $ atteint l'abscisse $ x=L $. En ce point ($ x=L, t=t_e $), nous avons d'après (8):
$ (9)\quad L= \frac{\alpha}{i} {(it_e)}^{\beta+1} $
d'où l'expression du temps d'obtention du régime permanent:
$ <br /> (10)\quad t_e= \frac{1}{i} \left ( {\frac{Li}{\alpha}} \right )^{1/(\beta+1)} $
Numériquement, nous obtenons $ t_e\simeq 530s $
Ainsi le régime permanent en tout point du domaine est obtenu pour $ t>t_e,\forall x $ la courbe caractéristique supérieure ancrée en $ x=0 $ délimite 2 domaines:
- un domaine inférieur où le régime est transitoire
- un domaine supérieur en $ t $ où en chaque point du domaine un régime permanent est établi. En $ x=0 $ le débit est nul alors qu'en $ x=L $ le débit est maximal.
De manière plus générale, exprimons le débit le long de chaque caractéristique:
$ (11)\quad q=\alpha{it}^{\beta+1} $
Or toujours le long de la caractéristique :
$ (12)\quad(it)^{\beta+1}=(x-x_A)\frac{i}{\alpha} $
ce qui conduit à l'expression du débit en tout point $ q=(x-x_A)i $
.
Ainsi, en tout point $ x $ du plan incliné, le débit est proportionnel à la distance entre ce point $ x $ et le pied de la caractéristique $ x_A $ qui passe par ce point.
Nous retrouvons donc bien le débit à l'exutoire qui arrive en $ x=L $ au temps $ t=t_e $.
Nous pouvons donc écrire au niveau de l'exutoire:
$ (13)\quad \begin{cases} q(L,t)=\alpha(it)^{\beta+1} &\quad \text{pour}\quad t<t_e \\ q(L,t)=\alpha(it_e)^{\beta+1} &\quad \text{pour} \quad t\geq t_e \end{cases} $
En tout point du domaine, il en est également de même.
Pour tracer l'hydrogramme en un point particulier $ (x_\delta,t_e) $, il faut déterminer l'instant correspondant au régime permanent $ t_e $ en ce point qui est donné par la caractéristique supérieure (caractéristique partant de $ x=0 $).
L'état d'équilibre est atteint pour chaque point du domaine en des instants différents, bien que la courbe de montée de l'hydrogramme soit identique en tout point. Nous pouvons donc écrire (d'après (12)):
$ (14)\quad \begin{cases} q(x_\delta,t)=\alpha(it)^{\beta+1} &\quad \text{pour} \quad t<t_e \quad \text{(transitoire)} \\ q(x_\delta,t)=ix_\delta &\quad \text{pour} \quad t\geqslant{t_e} \quad \text{(permanent)} \end{cases} $
Le temps d'équilibre est donné par :
$ (15)\quad t_\delta=\frac{1}{\alpha}\left ( \frac{x_\delta i}{\alpha} \right)^{1/(\beta+1)} $
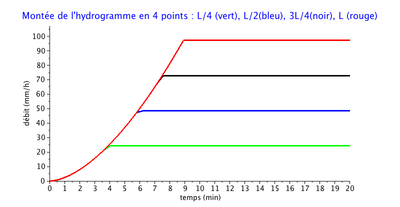
Ceci nous permet de tracer les hydrogrammes en 4 points du domaine, respectivement en x=L/4,L/2,3L/4,L (voir figure 2).
De même, nous pouvons tracer l'évolution temporelle du niveau de la hauteur d'eau sur l'ensemble du domaine:
$ (16)\quad \begin{cases} h(x,t)=it &\quad \text{pour} \quad t<t_\delta \quad \text{(transitoire)} \\ h(x,t)= \left ( \frac {ix} {\alpha} \right)^{1/(\beta+1) } &\quad \text{pour} \quad t\geqslant{t_e} \quad \text{(permanent)} \end{cases} $
Pour cela, nous balayons le plan des caractéristiques par pas de temps constants pour obtenir l'abscisse correspondant à ce temps sur chaque caractéristique afin d'obtenir le triplet $ (x,t,h) $ (voir § 4.2.2)
Tarissement de l'hydrogramme
Lorsque la pluie s'arrête ($ i=0, t=1200s $), le débit est permanent.
Le système d'équations se réduit alors à :
$ <br /><br /> (17)\quad \begin{cases} \frac{\partial h }{\partial t}+\alpha (\beta+1) h^\beta \frac{\partial h }{\partial x}=0\\ q(x,t)=ix \end{cases} $
Les caractéristiques sont cette fois-ci des droites le long desquelles $ h=cste $. Elles peuvent donc être facilement déterminées connaissant :
- le pied de la caractéristique qui correspond au débit permanent à $ t_c=1200 s $.
$ (18)\quad q_e=ix \Rightarrow h_e=\left ( \frac {q_e} {\alpha} \right)^{1/(\beta+1) } $
- un point extrémité en temps que nous choisirons à $ t_{fin}=40 mn $
L'examen des pentes des caractéristiques montre qu'elles dépendent de l'abscisse $ x_p $ du pied de la caractéristique:
$ (19)\quad \frac {dx} {dt}=pente(x=x_p)=(\beta+1) \left ( \frac {ix_p} {\alpha} \right)^{\beta/(\beta+1) } $
Ainsi, la pente de la caractéristique en $ x=0 $ : $ pente(x=0)=0 $, ce qui donne une droite caractéristique verticale. Physiquement, cela signifie que la goutte de pluie qui tombe en ce point met en temps infini pour atteindre l'exutoire.
Ceci explique l'allure du faisceau de caractéristiques de la figure suivante, que nous avons tracé pour des valeurs de $ x $ en progression géométrique telles que:
$ (20)\quad x_n=10^n \quad \text{avec} \quad n\in (-5,2) mod (0,2) $
L'abscisse extrémité $ x_p^{fin} $ est donnée pour chaque caractéristique de pied $ x_p^{0} $ par:
$ (21)\quad x_p^{fin}=x_p^0+{\alpha}(\beta+1) \left ( \frac {ix_p^0} {\alpha} \right)^{\beta/(\beta+1) } t_{fin} $
Ces caractéristiques sont représentées sur la figure 3.
Évolution du débit à l'exutoire
Le débit à l'exutoire $ x=L $ est fourni par l'intersection des caractéristiques avec la verticale en $ x=L $.
Le temps est donné par l'expression suivante :
$ <br /> (22)\quad t_p^L= \frac {L-x_p^0} {\alpha(\beta+1)} \left ( \frac {ix_p^0} {\alpha} \right)^{-\beta/(\beta+1) } $
Il en est de même aux abscisses $ L/4 $,$ L/2 $, $ 3L/4 $.
Les hydrogrammes de tarissement au droit de ces abscisses sont représentés sur la figure 4.
Évolution du niveau d'eau sur le plan incliné
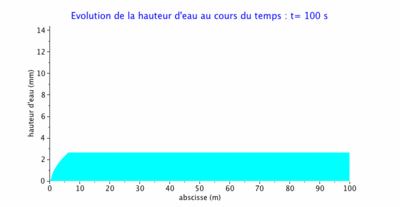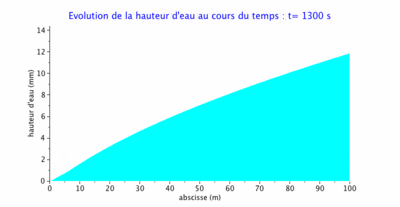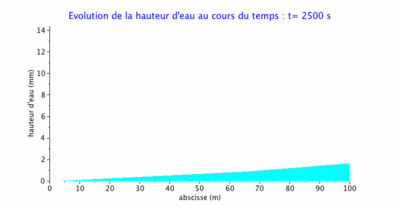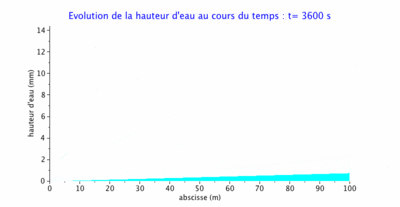
Nous présentons ci-dessous 3 états du niveau d'eau sur le plan incliné:
- au temps $ t=300s $ qui correspond à la montée de l'hydrogramme;
- au temps $ t=1200s $ qui correspond à la fin de la période de pluie. Le domaine est complètement en eau et caractérisé par un régime permanent;
- au cours du tarissement, le plan incliné est en phase de vidange.
Ces courbes ont été tracées de la manière suivante:
- nous choisissons la distribution des pieds des caractéristiques $ x_p $ : linéaire pour la montée et exponentielle pour la descente (relation (20));
- nous nous déplaçons sur chaque caractéristique par pas de temps constants : pour la montée, la hauteur d'eau est donnée par $ h=it $ et pour le tarissement $ h=cste $
- nous obtenons une matrice $ (x,t) $ pour toutes les valeurs de $ h_p $;
- nous traçons ensuite $ x(h_p) $ pour différentes valeurs de t.
En examinant les figures ci-dessous, nous pouvons faire les remarques suivantes:
- en phase de montée, le domaine se remplit en chaque point d'abscisse par une accumulation verticale de la pluie, mais également par superposition des eaux en provenance de l'amont;
- le régime permanent est très stable;
- en phase de tarissement, nous pouvons observer une rapide descente du niveau d'eau, tout particulièrement à l'aval. L'amont a du mal à se vider (voir remarque précédente), mais les lames d'eau résiduelles restent très faibles.
L'animation ci-après représente l'évolution de l'épaisseur de la lame d'eau au cours des 3 phases : montée, régime permanent et tarissement.
Conclusions
Dans cette fiche consacrée à la mise en évidence du comportement d'un plan incliné de pente uniforme soumis à une pluie constante et homogène, nous avons étudié la génération, la propagation et l'évacuation de l'eau.
Nous avons étudié les phases de chargement de l'hydrogramme pendant la durée de la pluie jusqu'à obtenir un régime permanent.Nous avons ensuite étudié le tarissement généré par l'arrêt de la pluie jusqu'à évacuation de l'eau sur le plan incliné.
En ce qui concerne les méthodes d'analyse numérique utilisées, nous avons tout particulièrement mis en oeuvre :
- la méthode des caractéristiques
Les résultats obtenus sont satisfaisants par rapport à ce que nous avons pu lire dans la littérature.
Des prolongement de cette étude peuvent être envisagés notamment avec le couplage de ce modèle analytique avec un modèle d'écoulement dans les sols, pour mettre en évidence les processus de ruissellement - infiltration que nous observons dans les bassins hydrologiques et qui sont souvent à l'origine de crues.
Références bibliographiques
- Pierre-Alain Roche, Jacques Miquel, Eric Gaume, "Hydrologie quantitative - Processus, modèles et aide à la décision", Springer-Verlag, juin 2012, 590 pages.
- Thomas Esclaffier (notes non publiées).
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS