Modèle d'agitation dans les ports
Sommaire |
Hypothèses
L’agitation de houle dans les ports est basée sur un grand nombre d’hypothèses sur le fluide afin de faciliter la modélisation sur des domaines de calcul qui restent grands (de l’ordre du kilomètre carré). Les hypothèses les plus souvent retenues sont les suivantes :
- le fluide est parfait, incompressible et irrotationnel.Un potentiel des vitesses $ \phi(x,y,z,t)\, $ est alors introduit tel que $ V= \nabla \phi\, $ avec $ V(x,y,z,t)\, $ le vecteur des vitesses ;
- les sollicitations atmosphériques à la surface libre (gradient de pression et vent) sont négligées ;
- le fond est fixe et imperméable ;
- la hauteur de la houle est faible à la fois par rapport à sa longueur d’onde et à la profondeur ;
- la théorie spectrale de la houle est applicable de telle sorte que le problème peut se ramener à des calculs de houle monochromatique. La pulsation de la houle est notée $ \omega\, $.La notation complexe est alors utilisée en prenant la convention suivante:
$ \Phi (x,y,z,t)= \mathfrak{R}\Big[\Psi(x,y,z)e^{-j\omega t}\Big] $
- l’hypothèse de pente douce est appliquée afin de négliger les ondes dites évanescentes, les effets de pente et de courbure d’ordre 2. Le potentiel complexe des vitesses $ \Phi\, $ s’exprime alors en fonction du potentiel complexe horizontal $ \Psi\, $ et du premier mode vertical dit propagatif sous la forme suivante
$ \Phi(x,y,z)=\Psi(x,y)\frac{\cosh \Big[k(Z+h)\Big]}{\cosh \Big[kh\Big]} $ où k est l’unique solution réelle de l’équation de dispersion $ \omega^2=gk tanh [kh]\, $, h la profondeur et g la gravité.
Equation de pente douce ou modèle de Berkhoff
L’équation de pente douce a été obtenue en 1972 par Berkhoff. C’est une équation différentielle sur le potentiel complexe horizontal $ \Psi\, $:
$ \nabla \Big(c c_g \nabla \Psi \Big ) + k^2 c c_g \Psi =0 $
Sur fond plat, l’équation de Helmholtz est retrouvée:$ \nabla\Psi+k^2\Psi=0 $
L’équation de Helmholtz est en général résolue par équation intégrale. Le domaine portuaire peut être modélisé sous la forme de sous-bassins avec une bathymétrie portuaire à fonds constants par morceaux. Cette méthode a été beaucoup utilisée dans le passé (ex modèle HYPO 41 de SOGREAH – Agostini (1992)) et est le plus souvent abandonnée au profit de modèles basés sur l’équation de pente douce résolue par éléments finis.
Des modèles analytiques ont aussi été utilisés dans le passé basés sur des tracés de rayons sur fonds plats avec solutions analytiques de diffraction et réflexion sur les frontières (ex modèle DIFFRA du CETMEF).
L’ingénieur s’intéresse d’abord à la hauteur de houle H qui correspond à la hauteur entre crêtes et creux de la surface libre. L’équation dynamique à la surface libre donne la relation entre H et le module du potentiel complexe horizontal : $ \Psi: H= 2\omega\frac{|\Psi|}{g} $
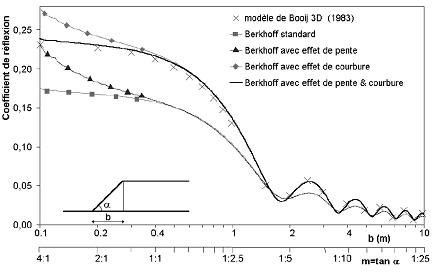
Deux termes d’effet de pente en $ |\nabla h|^2 $ et de courbure en $ \nabla^2 h $ sont négligés dans l’équation classique de pente douce. Si l’on regarde en détails, ces termes ont cependant un effet nbsp;significatif sur les résultats des modèles. Ils ont été calculés par Massel (1994, 1996), Chamberlain et Porter (1995), Chandrasekara et Cheung (1997) et Suh et al. (1997).
Benoit (1999) a retenu les expressions de Chamberlain et Porter (1995) et montré (voir Figure 1) à partir des résultats du modèle linéaire de Booij (1983) qui résout l’équation tridimensionnelle de Laplace, d’une part que la limite de pente traditionnellement admise 1:3 pour les modèles de Berkhoff est surestimée et d’autre part que les effets de pente et de courbure d’ordre 2 améliorent très sensiblement la précision du modèle.
L’équation de pente douce peut s’exprimer en utilisant le module $ A\, $ et la phase $ S\, $ du potentiel complexe $ \Psi = Ae^{jkS}\, $. La partie réelle de l’équation de pente douce s’écrit alors $ |\overrightarrow{\nabla S}|^2=k^2+\frac{\nabla A}{A} + \frac{\nabla cc_g}{cc_g}.\frac{\nabla A}{A} $. Les deux derniers termes sont associés au phénomène de diffraction et distinguent l’équation de pente douce de l’équation eikonale qui régit la réfraction de la houle.
Conditions aux limites
L’onde incidente $ \Psi^{inc} \, $ est une onde plane régulière (c’est-à-dire monochromatique et monodirectionnelle) de période $ T\, $, de direction $ \alpha_{inc} \, $ par rapport à l’axe Ox et d’amplitude $ \Psi_0 = \frac{gH_ {inc}}{2\omega} $ où $ H_{inc} \, $ est la hauteur de la houle incidente. L’onde incidente s’écrit donc $ \Psi^{inc}=\Psi_0 e^{jk(x \cos \alpha_{inc}+y \sin \alpha_{inc})} $
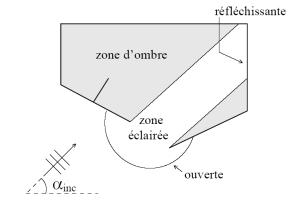
La frontière du domaine est formée de frontières de deux types principaux (voir figure 2) :
- Les frontières réfléchissantes constituées essentiellement par les ouvrages portuaires
- Les frontières ouvertes en entrée ou en sortie
Dissipation de la houle
L'équation de pente douce avec dissipation s'écrit de la façon suivante:
$ \nabla \Big(c c_g \nabla \Psi \Big ) + k^2 c c_g \Psi = - j \omega (W_{def}+W_{fond}+ W_{poreux} ) $
où $ W_{def} \, $, $ W_{fond} \, $, et $ W_{poreux} \, $ sont la dissipation par respectivement déferlement, frottement sur le fond et percolation dans les fonds poreux.
Les trois modes principaux de dissipation de la houle sont en effet les suivants:
- dissipation par déferlement
- dissipation par frottement sur le fond
- dissipation par percolation dans les fonds poreux
Houle aléatoire
La houle réelle n’est pas monochromatique, c’est à dire définie par une seule période. Elle se propage aussi selon plusieurs directions plus ou moins proches. La représentation dite régulière de la houle n’est donc pas toujours réaliste. Il faut donc utiliser une représentation irrégulière de la houle que l’on appelle encore houle aléatoire ou houle réelle.
Il existe deux approches de la houle aléatoire :
- une approche statistique
- une approche spectrale
Résolution de l'équation de pente douce
Le modèle numérique est construit à partir de l’équation de Berkhoff et des conditions aux limites présentées dans les sections précédentes.
Les méthodes numériques appliquées peuvent être:
- la méthode des éléments finis
- la méthode des différences finies
- la méthode des volumes finis
Applications
Après application des conditions aux limites sur les bords ouverts et semi-réfléchissants, le calcul des angles d’incidence aux frontières et maillage aux éléments finis, le code de calcul fournit le module et la phase de la hauteur de houle complexe en houle régulière, il estime la hauteur de houle significative ainsi que les paramètres associés en houle réelle.
- Exemple du port de Brest
Exemples de modèles
En France,
- le modèle REFONDE est le modèle d’agitation de houle du CETMEF et de l'UTC
- le modèle ARTEMIS est le modèle d’agitation de houle de EDF-LNHE
A l’étranger,
- le modèle MIKE 21 – Elliptic Mild Slope (EMS) module du Danish Hydraulic Institute (DHI)
- le modèle PHAROS de Delft Hydraulics (WLDELFT)
Références
Agostini, P., 1992, Notice d’utilisation du programme HYPO 41. Notice STC INF n° 92.05, 77 p
Battjes, J.A., 1974, Computation of set-up, longshore currents, run-up and overtopping due to wind-generated waves. Thèse de techn. Univ. Delft, 244 p
Battjes, J.A. et Janssen, G.,1978, Energy loss and set-up due to breaking of random waves. Proceedings de la 16ème conférence internationale de Coastal Engineering, Hambourg, pp 569 - 587
Benoit, M., 1994, Mesures de réflexion de houle en incidence oblique sur une digue à talus.. Rapport EDF/LNHE HE-42/94/36
Benoit, M., 1999, Extension de l’équation de réfraction-diffraction de Berkhoff pour traiter des bathymetries rapidement variables. Rapport EDF/LNHE HE-42/99/049/A
Beltrami G.M., Bellotti, G., De Girolamo, P. et Sammarco, P., 2001, Treatment of wave breaking and total absorption in a mild slope equation FEM model. J. Waterway, Port, Coastal and Ocean Eng., Vol 127 (5), pp 263-271
Berkhoff, J.C.W., 1972, Computation of combined refraction and diffraction. Proceeding of the 13th International Coastal Engineering Conference, ASCE, pp 471-490
Booij, N., 1983, A note on the accuracy of the mild slope equation. Coastal Eng., Vol. 7, pp 191-203
Chamberlain, P.G. et Porter, D., 1995, The modified mild slope equation. J.Fluid Mech., Vol 291, pp 393-407
Chandrasekara, C.N. et Cheung, K.F., 1997, Extended linear refraction-diffraction model. J. Waterway, Port, Coastal and Ocean Eng., Vol 123 (5), pp 280-286
Cruz, E.C., Isobe, M., Watanabe, A. ,1997, Boussinesq equations for wave transformation on porous beds. Coast. Eng., 30, pp 125-156.
Dingemans, M.W., 1997, Water wave propagation over uneven bottoms. Advanced series on ocean Engineering. Vol. 13. World Scientific. 471 p.
Dalrymple, R.A., Losada, M.A. et Martin, P.A., 1991. Reflection and transmission from porous structures under oblique wave attack. J. Fluid Mech., Vol 224, pp 625-644
Givoli, D., 1992, Numerical methods for problems in unbounded domains. Elsevier. Amsterdam.
Goda, Y., 1975, Irregular wave deformation in the surf zone. Coastal Eng. Jpn., Vol 18, pp 13-26
Goda, Y., 1985, Random seas and design of maritime structures. University of Tokyo Press
Gu, G.Z. et Wang, H., 1992. Numerical modelling for wave energy dissipation within porous submerged breakwaters of irregular sections. Coast. Eng. Conf. Proc., pp 1189-1199.
Hasselmann, D.E., Dunckel M., Ewing, J.A., 1980. Directional Wave Spectra Observed during JONSWAP 1973. Journal of Physical Oceanography, pp 1264–1280
Houari, M., 2002, Etude des conditions aux limites dans un modèle numérique d’agitation de houle. Thèse de doctorat de l’Ecole Nationale des Ponts et Chaussées
Houari, M., Sergent, P. et Duhamel, D. , 2003. Réflexion sur les ouvrages: modèle de houle à dissipation. Revue Française de Génie Civil, 7 (9), pp 1077-1097
Isaacson, M. et Qu, S., 1990, Waves in harbours with partially reflecting boundaries. Coastal Eng., Vol 14, pp 193-214
Losada, I.J., Silva, R. et Losada, M.A., 1996. 3D non-breaking regular wave interaction with submerged breakwaters. Coast. Eng. 28, 229-248.
Madsen, O.S., 1974, Wave transmission through porous structures. J. Waterw., Port, Coast., Ocean Eng. Vol 100 (3), 169-188.
Massel, S.R., 1994, Measurement and modelling of waves incident on steep islands ot shoals. Proceedings Int. Symp., waves – Physical and numerical modelling. Vancouver (Canada), Vol 2, pp 982-991
Massel, S.R., 1996, Ocean surface waves: their physics and prediction, Advanced series on Ocean Engineering, Vol.11, World Scientific, 492 p
Miche, R., 1944, Mouvements ondulatoires de la mer en profondeur constante ou décroissante forme limite de la houle lors de son déferlement. Application aux digues maritimes, Annales des Ponts et Chaussées, 285-319
Munk, W.H., 1949, The solitary wave and its application to surf problems, N.Y Acad. Sci., Vol 1 : 376-424
Panchang, V., Chen, W., Xu, B., Schlenker, K., Demirbilek, Z. et Okihiro, M., 2000, Exterior bathymetric effects in elliptic harbour models. J. Waterway, Port, Coastal structures, Vol 126(2), pp 71-78
Pierson, W.J. et Moskowitz, L., 1964, A proposed spectral form for fully developed wind seas based on the similarity theory of S.A. Kilaigorodskii. J Geophys Res, Vol, pp 5181-5190
Rojanakamthorn, S., Isobe, M., Watanabe, A., 1990. Modelling of wave transformation on submerged breakwater. Coast. Eng. Conf. Proc., pp1060-1073.
Ropert, F., 1999. Modélisation du comportement hydraulique des caissons Jarlan. Thèse de doctorat de l’Université de technologie de Compiègne.
Seelig, W.N. et Ahrens, J., 1981, Estimation of wave reflection and energy dissipation coefficients for beaches, revetments and breakwaters. US army corps of Engineers CERC, Fort-Belvoir, V.A. (USA)
Seelig, W.N., 1983, Wave reflection from coastal structures. J. Waterway, Port, Coastal structures, Vol 83, pp 961-973
Sergent, P., Ropert, F., Orcel, O., Houari, M., Duhamel, D. et Dhatt, G., 2002, Water waves in harbours areas: appreciation of open boundaries. J. Waterway, Port, Coastal structures, Vol 128 (5), pp 184-189
Sergent, P. et Duhamel, D., 2006, Influence d’un coefficient de frottement dépendant de la profondeur sur la propagation des vagues sur un lit poreux. 9èmes J. Gén. Civ. Gén. Côtier, Brest
Silva, R., Salles, P. et Palacio, A., 2002. Linear waves propagating over a rapidly varying finite porous bed. Coast. Eng. 44, pp 239-260.
Sollit, C.K. et Cross, R.H. ,1972, Wave transmission through permeable breakwater. Coast. Eng. 13, pp 1827-1846.
Stewart, D.R. et Panchang, V.G., 2001, Improved coastal boundary conditions for surface water waves. Ocean Eng., Vol 28 (1), pp 139-157
Sutherland, J. et O’Donoghue, T., 1998, Wave phase shift at coastal structures. J. Waterway, Port, Coastal structures, Vol 124(2), pp 90-98
Xu, B., Panchang, V. et Demirbilek, Z., 1996, Exterior reflections in elliptic harbour wave models. J. Waterway, Port, Coastal structures, Vol 122(3), pp 118-126
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS