Réflectivité radar (HU)

Traduction anglaise : Radar reflectivity

Dernière mise à jour : 28/07/2025

Mesure de la part du rayonnement émis par un radar qui est réfléchie vers l'antenne.

Réflectivité radar des précipitations

Le principe de la détection radar des précipitations est lié au comportement des molécules d’eau soumises à un champ électromagnétique. Dans ces conditions, ces molécules se comportent comme des dipôles oscillants (c'est à dire des antennes) qui captent puis réémettent à la même fréquence que celle qu'elle reçoive. L’énergie ainsi rétrodiffusée de manière isotrope dans l’espace par ces multiples antennes permet la détection radar. L’eau n’est cependant pas un diffuseur parfait et disperse sous forme de chaleur une partie de l’énergie qu’elle capte. Ce mécanisme est responsable de l’atténuation du signal radar par les précipitations.

La taille relative des hydrométéores (gouttes, flocons, grêlons) par rapport à la longueur d’onde $ λ $ détermine les propriétés de diffusion (il en est de même pour celles d’atténuation qui ne sont pas décrites ici). Dans le cas simple où la taille des hydrométéores est faible par rapport à $ λ $ (hypothèse dite de Rayleigh, acceptable pour la pluie en bande C et S), la section efficace de rétrodiffusion radar $ σ_r $ d’une particule sphérique de diamètre $ D_r $, c’est à dire la surface qu’aurait cette particule si elle était un diffuseur parfait, s’écrit :

$ σ_r = \frac{π^5}{λ^4}.K^2.D_r^6 \qquad (1) $

$ K $ étant la constante diélectrique de l'hydrométéore qui dépend de son état et de sa température. En particulier l’eau liquide a une capacité environ cinq fois plus forte que la glace à rétrodiffuser en raison de la mobilité des molécules qui peuvent s’orienter par rapport au plan de polarisation des ondes.

Lorsque de multiples hydrométéores sont réparties dans un volume donné, leurs sections efficaces de rétrodiffusion s’additionnent pour donner la capacité de diffusion globale de l’ensemble que l’on appelle la réflectivité radar :

$ η_r = \sum_i{σ_{ri}}\qquad (2) $

Pour interpréter cette valeur de réflectivité en terme de précipitation, plusieurs hypothèses sont nécessaires, en particulier :

• le volume sondé est complètement rempli d’hydrométéores de même type pour ne pas moyenner le signal sur des cibles différentes ;
• le taux de précipitation est le même dans tout le volume.

Ceci nécessite que la largeur du faisceau soit faible et l’impulsion courte afin d’avoir la plus petite cellule de résolution possible.

Si l’on fait alors l’hypothèse que la constante diélectrique de tous les hydrométéores du volume sondé est la même et que leur distribution volumique en taille est définie par la fonction de répartition $ N(D_r) $, on peut définir le facteur de réflectivité radar $ Z $ par :

$ Z = \int_{D_{rmin}}^{D_{rmax}}{N(D_r).D_r^6.dD_r}\qquad (3) $

où $ D_{rmin} $ et $ D_{rmax} $ bornent la gamme de diamètres de gouttes considérée. La réflectivité s’exprime en mm⁶/m³.

Comme cette valeur absolue de réflectivité peut varier de plusieurs ordres de grandeurs en fonction de la taille et de la densité des hydrométéores, on préfère le plus souvent utiliser une échelle logarithmique en la normant par rapport à la réflectivité d'une cible standard : $ Z_0 $ = 1 mm⁶/m³. Cette valeur correspond à la réflectivité d'une cible sphérique de 1 mm de diamètre (taille moyenne des gouttes d'eau) dans un volume de 1 m³ ; on parle alors de dBz (relation 4) :

$ Z(dBz) = 10.log\frac{Z}{Z_0}\qquad (4) $

Relation entre la réflectivité et l'intensité des précipitations

L'intensité de la pluie dépend de la taille des gouttes, de leur densité et de leur vitesse de chute. La vitesse de chute d'une goutte résulte de l’équilibre entre le poids de la goutte et la résistance de l'air à son déplacement. Elle est sensiblement proportionnelle à la racine carrée de son diamètre moyen.

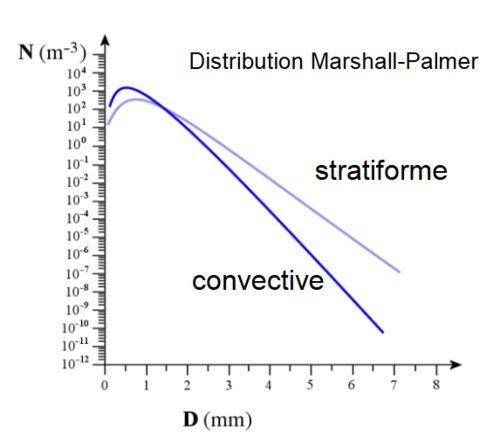
La réflectivité radar et l'intensité de la pluie dépendent donc toutes les deux de la distribution des gouttes de pluie en fonction de leur diamètre. On sait, depuis les travaux précurseurs de Marshall et Palmer (1948), que cette distribution dépend du type de précipitation et que, si on la trace en échelle semi-logarithmique (comme sur la figure 1), elle est proche d'une droite pour les tailles de gouttes supérieures à 1 mm.

Figure 1 : Exemples de distribution de Marshall-Palmer pour différents types de précipitations ; Source : Wolff et Vaillant (2011)

Dans ces conditions, il est possible d'établir une relation entre la réflectivité ($ Z $) et l'intensité ($ R $), sous la forme :

$ Z = a.R^b \qquad (5) $

ou

$ R = a{'}.Z^{b{'}} \qquad (6) $

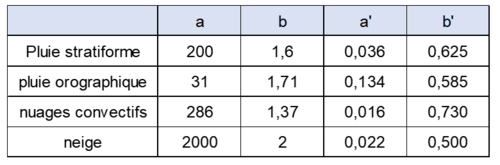
Les valeurs des paramètres $ a $ et $ b $ (ou $ a' $ et $ b' $) dépendent de la distribution des gouttes de pluie en fonction de leur diamètre. Elles devraient normalement être établies en mesurant la distribution granulométrique des gouttes pour chaque pluie particulière. Comme ce n'est techniquement pas possible, on utilise parfois des valeurs génériques (voir tableau de la figure 2).

Figure 2 : Valeurs des coefficients de la relation $ Z-R $ pour diverses situations ; $ Z $ est en dBZ et $ R $ en mm/h.

La relation la plus courante pour les latitudes moyennes est la relation de Marshal-Palmer :

$ Z = 120.R^{1{,}6} \qquad (7) $

Les valeurs des paramètres sont cependant le plus souvent ajustées à partir de mesures au sol. Voir article Radar hydrométéorologique (HU).

La réflectivité des précipitations en dBz varie en général entre 7 (pluie très faible, de l'ordre de 0,1mm/h) et 60 (pluie très forte, de l'ordre de 200mm/h) (figure 3).

Figure 3 : Relations entre dBZ et intensité de pluie et codes couleur associés ; Source : Wolf et Vaillant, 2011.

Bibliographie :

• Marshall, J. S., Palmer, W. McK. (1948) : The distribution of raindrops with size ; Journal of Meteorology ; N°5 ; pp 165-166 ; disponible sur https://journals.ametsoc.org/view/journals/atsc/5/4/1520-0469_1948_005_0165_tdorws_2_0_co_2.xml
• Wolff, C. et Vaillant, P. (2011) : Radartutorial ; Chapitre 2A : Radar météorologique ; 27p. disponible sur https://www.radartutorial.eu/druck/Chapitre2A.pdf