Utilisateur:Jean-Michel Tanguy/SujetENTPE2023/B33

Contexte

La houle représente une problématique dans les phénomènes d'érosion et sa hauteur est influencée par les phénomènes météorologiques comme des tempêtes, des ouragans, étant de plus en plus violents et de moins en moins rares. L'impact de la houle sur les côtes devient alors un enjeu majeur pour les gouvernements côtiers. De plus avec la montée des eaux, la houle peut représenter une menace d'autant plus importante pour les habitants et les infrastructures de zones de faible élévation. Antonio Guterres, secrétaire général de l'ONU, lance une alerte, le 14 février 2023 : "La montée des eaux représente un futur sombre,[...]. La montée des eaux menace des vies et met en péril l'accès à l'eau, à la nourriture et des soins de santé [...] surtout lorsqu'elle est combinée à des phénomènes météorologiques extrêmes". Il y a donc une réelle nécessité de développer des modèles précis du comportement de la houle et ainsi développer des infrastructures adaptées aux différentes situations.

LIEN DE LA VIDÉO

Modèle de Berkhoff et résolution analytique

Pour modéliser la propagation de la houle, on utilise le modèle de Berkhoff en bi-dimensionnel

$ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $

avec $ \phi $ le potentiel des vitesses complexe, $ k $ le nombre d’onde fonction de la profondeur H et de la fréquence $ \omega^2=gk \tanh(kH) $ , C est la célérité de l’onde, Cg est la célérité de groupe des vagues.

On se place dans le domaine d'étude des ondes longues, ce qui nous permet d'approximer $ C=C_g=\sqrt{gH} $.

Ce modèle nécessite la connaissance des conditions aux limites, c'est-à-dire les caractéristiques des frontières, si elles sont absorbantes ou réfléchissantes.

On note $ h(x,t)=\Re \left (\phi e^{-i\omega t} \right ) $ l'évolution dans le temps de la hauteur de houle.

Pour chaque cas, nous allons établir l'équation de Berkhoff et la résoudre analytiquement avec des méthodes de résolution d'équations différentielles classiques pour les cas n°1 et n°2.

Dans les cas n°3 et n°4, la résolution analytique fera alors appelle aux solutions d'une équation de type Bessel $ x^2\dfrac{\partial^2 y}{\partial x^2} + (2p+1) x\dfrac{\partial y}{\partial x} + (\alpha^2x^2-\beta^2) y = 0 $. Les solutions sont alors sous la forme $ y = x^{-p}[C_1J\dfrac{p}{r}(\alpha\dfrac{x^r}{r}) + C_2Y\dfrac{p}{r}(\alpha\dfrac{x^r}{r})] $avec $ C_1 $et $ C_2 $ des constantes à déterminer et $ J $et $ Y $ les fonctions de Bessel respectivement de première espèce et de seconde espèce.

On réalisera alors que les équations sont de plus en plus compliquées à résoudre analytiquement, d'où l'importance d'établir un modèle d'approximation de ces solutions.

Résolution par homotopie

La méthode d'homotopie permet d'approximer la fonction solution de l'équation de Berkhoff établie par une fonction polynomiale. Considérons l’équation différentielle suivante à résoudre :

$ L(u(x))=f(x)+N(u(x)), x \in \Omega $

avec les conditions limites: $ B(u,u_n=0), x \in \Gamma $

où L est un opérateur linéaire, N un opérateur non-linéaire et f les termes complémentaires de l’équation.

L'homotopie de Liao [9] est définie de la manière suivante :

$ (1-p)\left[ L(U(x,t);p)-L(u_0(x,t)) \right ] +H(p)\left[ L(U(x,t);p)-N(U(x,t),p)-f(x) \right] $

où $ p \in \left[0,1\right] $ est un paramètre qui varie de 0 à 1, u0 est une estimation initiale de la solution.

Lorsque p=0 nous retrouvons la solution initiale U=u0 et lorsque p=1, nous retrouvons la solution exacte.

La transformation de p de 0 à 1 qui conduit U(x) de la solution estimée à la solution exacte provient de la transformation de U(x) en série de Taylor

$ U(x)=u_0(x)+\sum_{m=1}^\infty u_m(x)p^m $ avec $ u_m(x)=\dfrac{1}{m!}\dfrac{\partial^mU(x,t;p)}{\partial p^m}\Bigr]_{p=0} $

La mise en œuvre de l’homotopie nécessite de faire des hypothèses sur la fonction H(p) qui permet notamment un ajustement des non-linéarités. Pour la méthode HAM « Homotopie Perturbation Method », que nous mettrons en œuvre: $ H(p)=1 $.

Cas n°1

On étudie le cas du canal monodimensionnel plat de longueur L.

On suppose une entrée par l’aval ( en $ x=0 $) d’une onde qui vérifie la condition de Dirichlet donc de fréquence unitaire $ \phi(x=0)=1 $ et une sortie libre en amont (en $ x=L $) qui vérifie la condition de Robin $ \phi_x(x=L)=ik\phi(x=L) $.

• Résolution analytique

Comme vu précédemment l’équation du modèle de Berkhoff en 1D devient alors l'équation différentielle du deuxième ordre suivante :

$  \phi_{xx}+k^2\phi=0  $ 

On a alors pour solution: $ \phi(x)={K_1}e^{ikx}+{K_2}e^{-ikx} $ avec $ ({K_1},{K_2}) \in \mathbb{C^2} $

Avec les conditions aux limites imposées on obtient,

$ \phi(x=0)=K_1+K_2=1 \Rightarrow K_2= 1-K_1 $

$ \phi_x(x=L)=ik\phi(x=L) $ $ \Rightarrow {ik}({K_1}e^{ikL}-{K_2}e^{-ikL}) = {ik}({K_1}e^{ikx} + {K_2}e^{-ikx}) $

Donc $ K_2 =0 $ et $ K_1=1 $

On obtient alors une première solution, $ \phi(x)=e^{ikx} $

Le potentiel est la partie réelle donc

$ \phi(x)=cos(kx)  $

• Résolution par homotopie

La relation d'homotopie s'écrit en choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle:

$ (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $

En injectant la décomposition en série entière $ \phi(x,p)=\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+p^3\phi_3(x)+... $ et sa seconde dérivée:

$ \phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+... $

Nous obtenons:

$ (1-p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+p^3\phi_3(x)+...)]=0 $

Il faut ensuite simplifier et écrire cette relation suivant les puissances de p croissantes. Cette relation étant valable quel que soit p, tous les coefficients devant les puissances de p sont donc nuls.

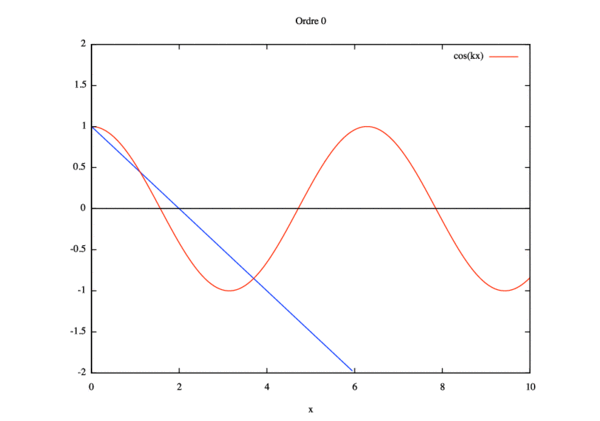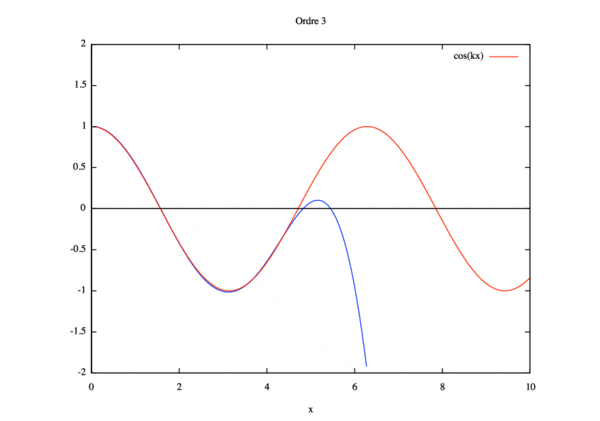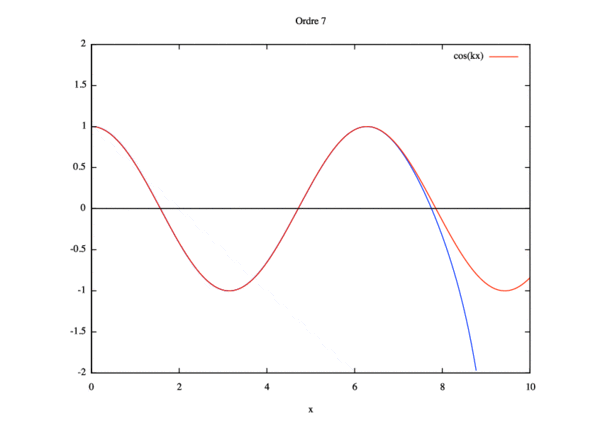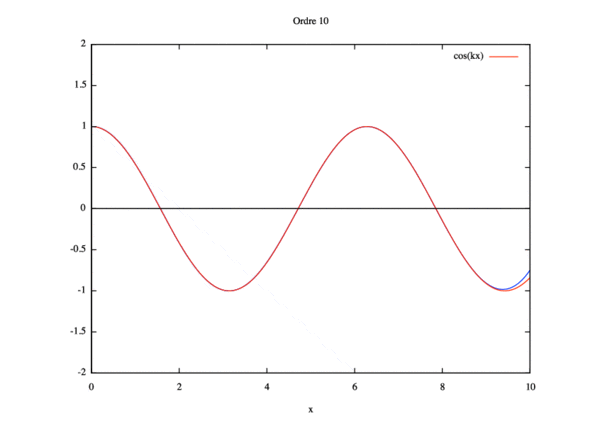
• • Ordre 0 :

$ \phi_{0,xx}=0 $ soit $ \phi_0=Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, il vient :

$ B=0 $

$ A= ik(AL+1) \Rightarrow A = \dfrac{ik}{1-ik} $

Donc

$ \phi_0(x)=1+\dfrac{ik}{1-ikL}x $ 

• • Ordre 1 :

$ \phi_{1,xx}-\phi_{0,xx}+\phi_{0,xx}+k^2\phi_0=0 $ soit $ \phi_{1}=-k^2\int\phi_0dxdx +Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $, il vient :

 $ \phi_1(x)=- \dfrac{k^2L(k^2L^2+3ikL-3)} {3(1-ikL)^2}x-k^2\left (\dfrac{ik} {6(1-ikL)}x^3+\dfrac{1} {2}x^2 \right ) $ 

• • Ordre 2 :

$ p^2 \phi_{2xx}(x)-p^2\phi_{1xx} + p^2\phi_{1xx} +k^2p^2\phi_{1xx} = 0 $

d'où $ \phi_{2xx}(x)=-k^2\phi_{1xx} $

Alors

$   \phi_{2}(x)= -k^2 \iint{\phi_1(x)dxdx} + Ax + B  $  

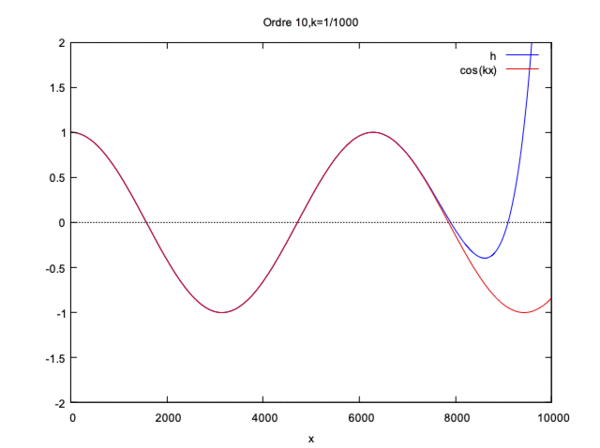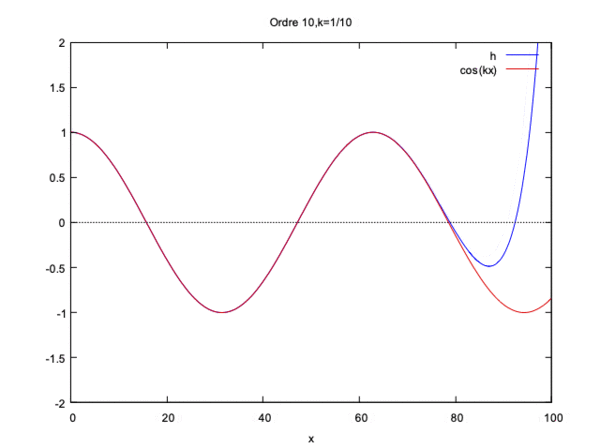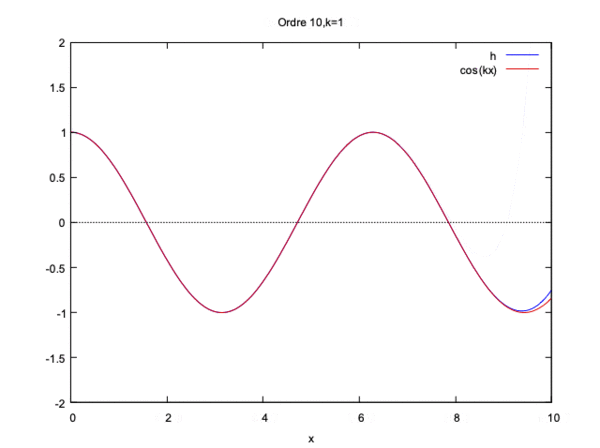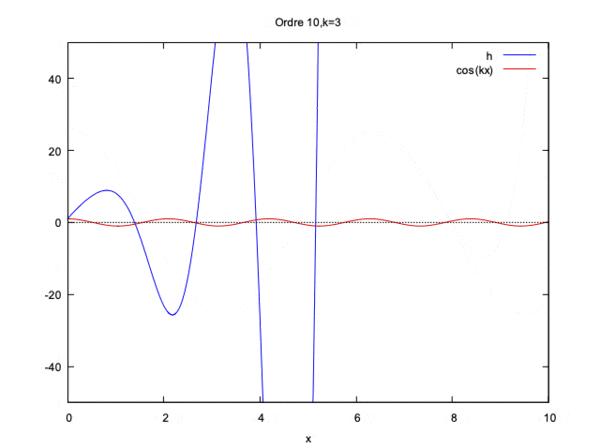
$ k=\dfrac{1} {100} $ (nombre d'onde en m^-1), $ H=40 $ (profondeur en m), $ c=\sqrt{gH} $ (célérité de l'onde en m/s), $ \lambda=\dfrac{2\pi}{k} $ (longueur d'onde en m), $ L=2\lambda $ (longueur du domaine en m).

• Étude de sensibilité

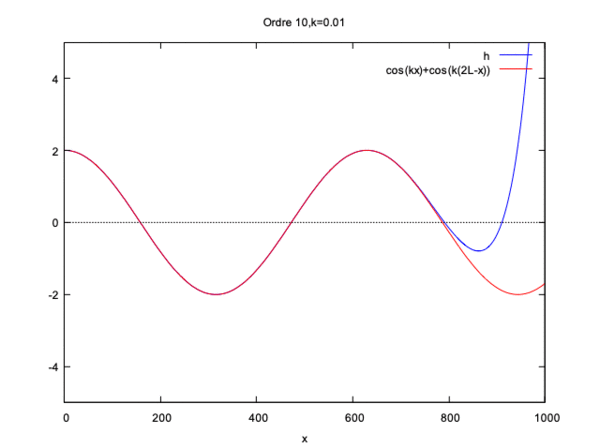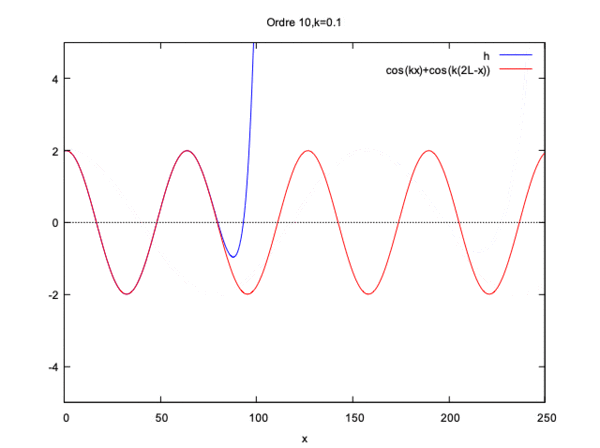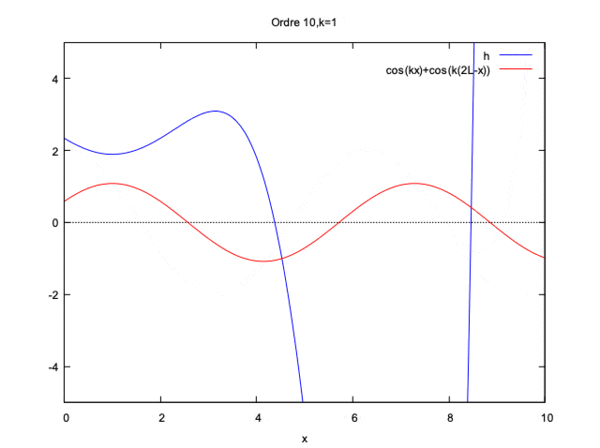
On remarque alors que la solution converge pour kL<<1 et pour kL=1 mais diverge si kL>1.

Cas n°2

On étudie un canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ \phi_x=ik(2-\phi) $ et réflexion totale amont $ \phi_x=0 $ .

• Résolution analytique

On obtient la même équation du modèle de Berkhoff vue dans le cas n°1,

$  \phi_{xx}+k^2\phi=0  $

$ \Rightarrow \phi(x)={K_1}e^{ikx}+{K_2}e^{-ikx} $ avec $ ({K_1},{K_2}) \in \mathbb{C^2} $

Seules les conditions aux limites changent,

$ \phi_x(x=0)=ikK_1 - ikK_2= ik(2-\phi(x=0)) \Rightarrow K_1-K_2= 2-K_1-K_2 \Rightarrow 2K_1=2 \Rightarrow K_1 =1 $

$ \phi_x(x=L)=0 \Rightarrow {ik}({K_1}e^{ikL}-{K_2}e^{-ikL}) = 0 \Rightarrow e^{ikL} - K_2e^{-ikL} =0 \Rightarrow K_2= e^{i2kL} $

d'où $ \phi(x) = e^{ikx} + e^{ik(2L-x)} $

Le potentiel est la partie réelle

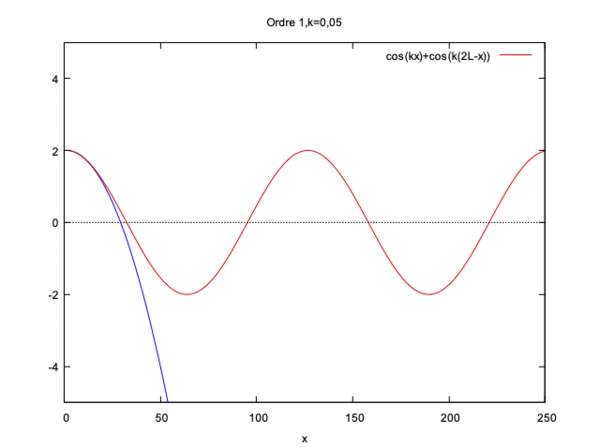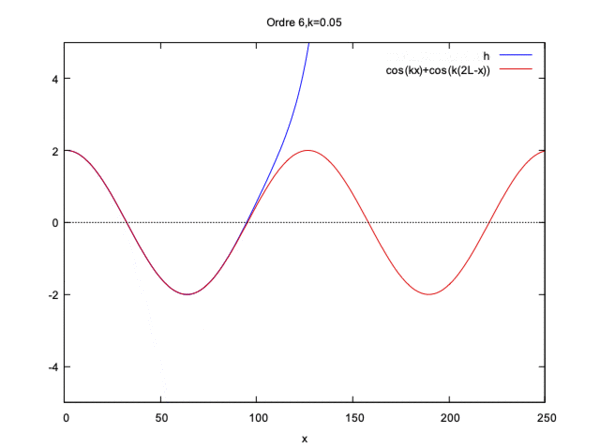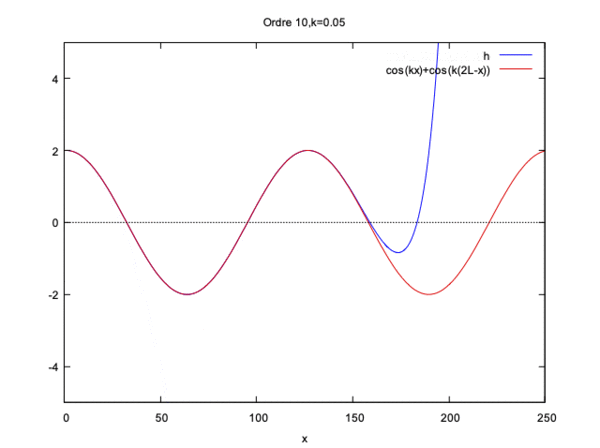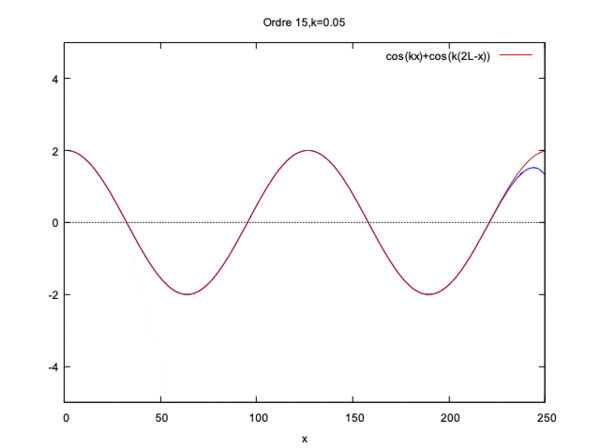
$  \phi(x)= cos(kx)+ cos(k(2L-x)) $

• Résolution par homotopie

$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+...)]=0 $

• • Ordre 0 :

$ \phi_{0,xx}(x)=0 $

En intégrant on obtient $ \phi_0(x)=Ax+B $

Avec les conditions aux limites : $ \phi_{0,x}^0=ik(2-\phi) $ et $ \phi_{0, x}^L=0 \Rightarrow A = 0 $ et $ B = 2 $

Donc

$  \phi_0(x)=2  $

• • Ordre 1 :

$ \phi_{1,xx}(x) = -k^{2}\phi_0(x) \Rightarrow \phi_1 (x) =- k^2x^2 + Ax + B $

Avec les conditions initiales données on a $ A = 2k^2L $ et $ B = 2ikL $ et donc :

$  \phi_1 (x) = - k^2x^2 + 2k^2Lx + 2ikL  $

• Étude de sensibilité

Cette fois si la solution converge seulement si kL<<1 et diverge si kL=1 ou kL>1.

Cas n°3

On étudie un canal monodimensionnel de longueur L avec pente du fond constante (s=cste) avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $ et sortie libre amont $ \phi_x=ik\phi $.

• Résolution analytique

Cas $ k = k_0 \sqrt{\dfrac{H_0}{H(x)}} $

On a $ C=C_g = \sqrt{gH(x)} $

Le modèle de Berkhoff devient alors

$ \nabla (gH(x) \nabla \phi ) + {k}^{2}gH(x)\phi = 0 \Leftrightarrow H(x) \Delta \phi - s \vec{grad} \phi + {k}^{2}H(x)\phi = 0 $

On réalise un changement de variable $ z = H_{0} -sx $

On obtient alors

$ \phi_{xx} - \dfrac{s}{H_0-sx}\phi_x +\dfrac{k_0^2}{H_0-sx}\phi = 0 $

d'où l'équation de type Bessel suivante :

$  z\phi_{zz} + \phi_z + {\alpha}^{2}\phi = 0  $ 

avec $ \alpha^{2} =\dfrac{{k_0}^{2}H_{0}}{s^2}, \frac{\partial \phi}{\partial x} = -s\phi_{z} $ et $ \frac{\partial^2 \phi}{\partial x^2} = s^2\phi_{zz} $

La solution est de la forme $ \phi(z) = [K_1J_0(2\alpha\sqrt{z})+K_2Y_0(2\alpha\sqrt{z})] $

Avec les conditions aux limites on a :

$ \phi(0)=1 \Leftrightarrow [K_1J_0(2\alpha\sqrt{H_0})+K_2Y_0(2\alpha\sqrt{H_0})] = 1 $

$ \phi_z(L) = ik \phi(L) $

En notant la dérivée première de $ J_0, J_1 $ et la celle de$ Y_0, Y_1 $ , on obtient

$ \phi_z(L) = \dfrac{\alpha s }{\sqrt{H_0-sL}} [K_1 J_1(2\alpha\sqrt{H_0-sL})+K_2Y_1(2\alpha\sqrt{H_0-sL})] = ik[K_1J_0(2\alpha\sqrt{H_0-sL})+K_2Y_0(2\alpha\sqrt{H_0-sL})] $

Il faut alors déterminer $ K_1 $ et $ K_2 $ :

On note alors $ J_0^0 = J_0(2\alpha\sqrt{H_0}), J_0^L = J_0(2\alpha\sqrt{H_0-sL}), Y_0^0= Y_0(2\alpha\sqrt{H_0}), Y_0^L = Y_0(2\alpha\sqrt{H_0-sL}) $ et de même pour $ J_1^0, J_1^L, Y_1^0, Y_1^L, $...

On a alors

$ K_1 = \dfrac{Y_1^L-iY_0^L}{ J_0^0 (Y_1^L -iY_0^L) + Y_0^0 (iJ_0^L- J_1^L)} $

et

$ K_2 = \dfrac{ iJ_0^L - J_1^L}{ J_0^0 (Y_1^L -iY_0^L) + Y_0^0 (iJ_0^L- J_1^L)} $

donc

$  \phi(z) =  \dfrac{Y_1^L-iY_0^L}{ J_0^0 (Y_1^L -iY_0^L) +  Y_0^0 (iJ_0^L- J_1^L)}  J_0(2\alpha\sqrt{z}) +   \dfrac{ iJ_0^L - J_1^L}{ J_0^0 (Y_1^L -iY_0^L) +  Y_0^0 (iJ_0^L- J_1^L)}  Y_0(2\alpha\sqrt{z})    $

• Résolution par homotopie

Toujours avec $ k = k_0 \sqrt{\dfrac{H_0}{H(x)}} $, on utilise la relation de Berkhoff obtenue précédemment pour établir la relation d'homotopie de la même manière que dans les cas précédents :

$ (1-p) \phi_{xx} + p[(H_0 -sx) \phi_{xx} -s\phi_{x} + k_0^2 H_0\phi] = 0 $

En injectant la décomposition en série entière de $ \phi(x,p), \phi_x(x,p), \phi_{xx}(x,p) $, on obtient :

$ (1-p) [\phi_{0,xx} +p \phi_{1,xx} + p^2 \phi_{2,xx} + ...] + p[(H_0 - sx)(\phi_{0,xx} +p \phi_{1,xx} + p^2 \phi_{2,xx} + ...) - s (\phi_{0,x} +p \phi_{1,x} + p^2 \phi_{2,x} + ... ) + {k_0}^{2}{H_0} (\phi_0 + p\phi_1 +p^2\phi_2+...)] $

• • Ordre 0 :

$ \phi_{0,xx} = 0 \Leftrightarrow \phi_0 = Ax + B $

or $ \phi_0(0) = B = 1 $ et $ \phi_{0,x}(L) = ik(AL+B) = A \Leftrightarrow A = \dfrac{ik}{1-ikL} $ , d'où

$  \phi_0 (x) = \dfrac{ik}{1-ikL}x + 1  $

• • Ordre 1 :

$ \phi_{1,xx} + (H_0-sx - 1 )\phi_{0,xx} - s \phi_{0,x} + k_0^2H_0 \phi_0 = 0 $

$ \Rightarrow \phi_{1,xx} = - (H_0-sx - 1 )\phi_{0,xx} + s \phi_{0,x} - k_0^2H_0 \phi_0 $

$ \Rightarrow \phi_{1,xx} = s \dfrac{ik}{1-ikL} - k_0^2H_0 ( \dfrac{ik}{1-ikL}x + 1 ) $

$ \Rightarrow \phi_{1,x} = s \dfrac{ik}{1-ikL}x - k_0^2H_0 \dfrac{ik}{1-ikL} \dfrac {x^2}{2} - k_0^2H_0 x + A $

$ \Rightarrow \phi_1 = s \dfrac{ik}{1-ikL}\dfrac{x^2}{2} - k_0^2H_0 \dfrac{ik}{1-ikL} \dfrac{x^3}{6} - k_0^2H_0\dfrac{x^2}{2} + Ax + B $

Avec les conditions initiales on obtient :

$ \phi_(0)= 0 \Rightarrow B = 0 $

et

$ \phi_{1,x}(L) = ik\phi_1(L) $

$ \Rightarrow A(1-ikL) = - \dfrac{sk}{1-ikL}(\dfrac{ikL^2}{2}-L) + k_0^2H_0 \dfrac{ik}{1-ikL}(\dfrac{L^2}{2} - \dfrac{ikL^3}{6}) + k_0^2H_0L(1-\dfrac{ik}{2}) $

$ \Rightarrow A= \dfrac{iksL}{(1-ikL)^2}(\dfrac{ikL}{2}-1) + \dfrac{k_0^2H_0L}{1-ikL}(1 - \dfrac{ik}{2}+\dfrac{ikL}{2(1-ikL)} + \dfrac{k^2L^2}{6(1-ikL)}) $

d'où

$ \phi_1(x) = s \dfrac{ik}{1-ikL}\dfrac{x^2}{2}  +  k_0^2H_0  \dfrac{ik}{1-ikL} \dfrac{x^3}{6} +  k_0^2H_0\dfrac{x^2}{2}  + \dfrac{iksL}{(1-ikL)^2}(\dfrac{ikL}{2}-1) + \dfrac{k_0^2H_0L}{1-ikL}(1 - \dfrac{ik}{2}+\dfrac{ikL}{2(1-ikL)} + \dfrac{k^2L^2}{6(1-ikL)})x   $

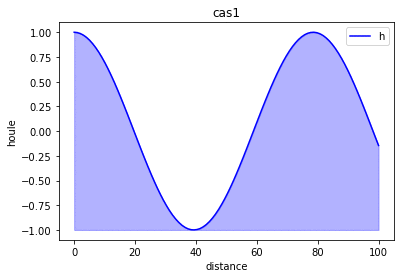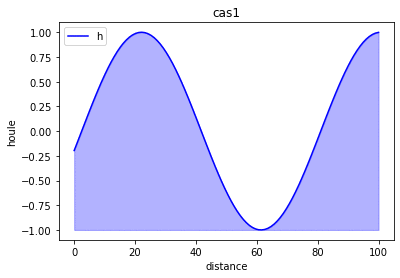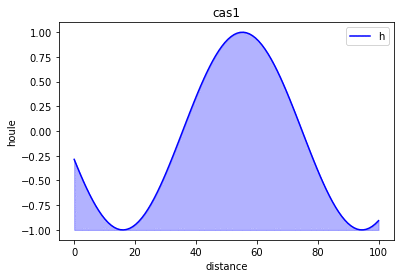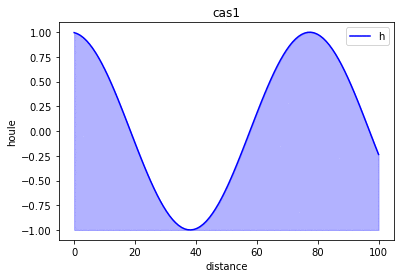
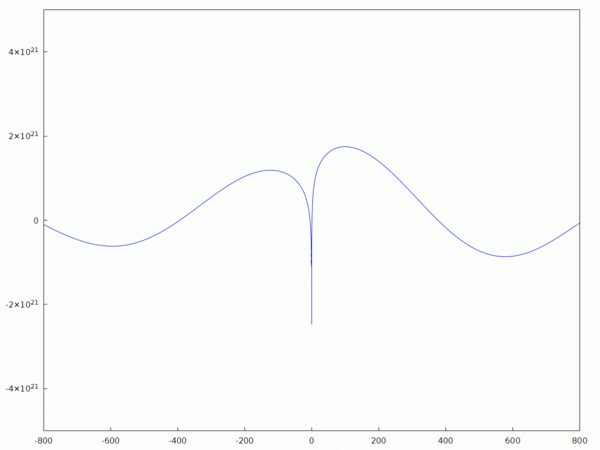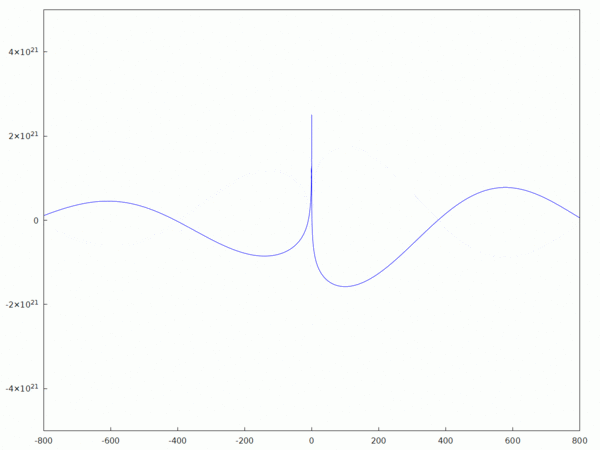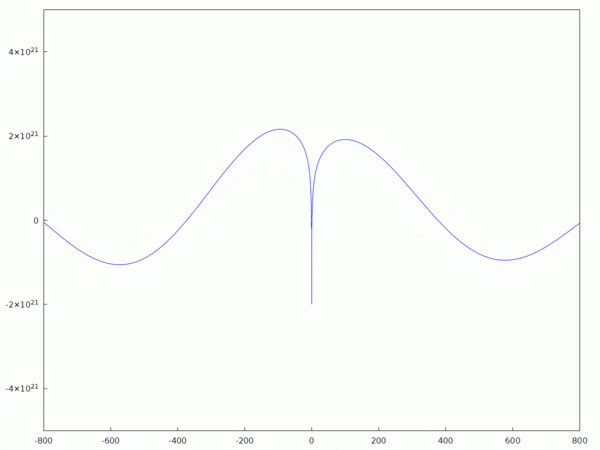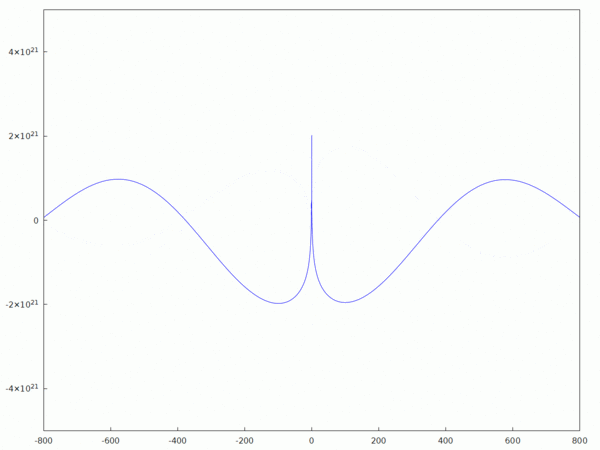
Courbe de la solution analytique

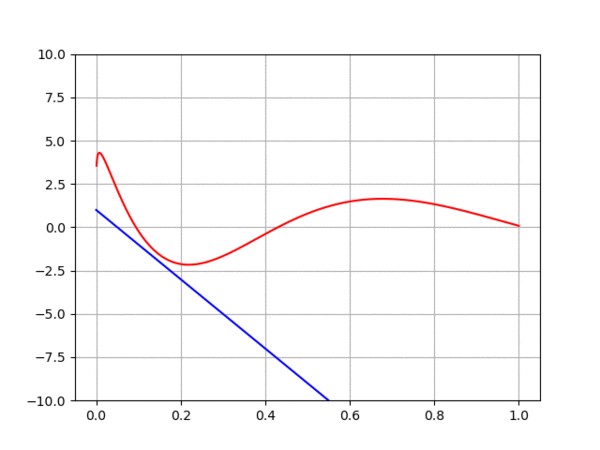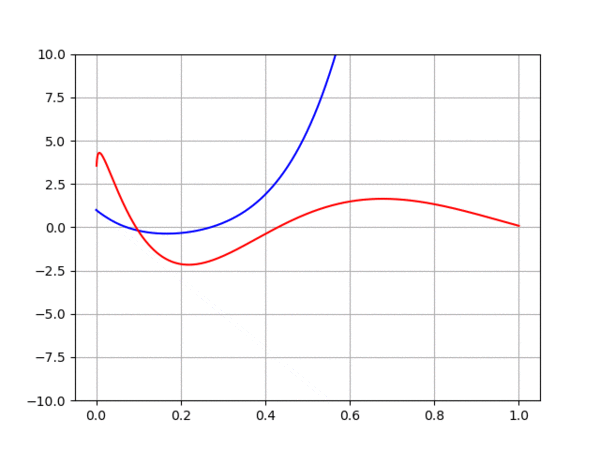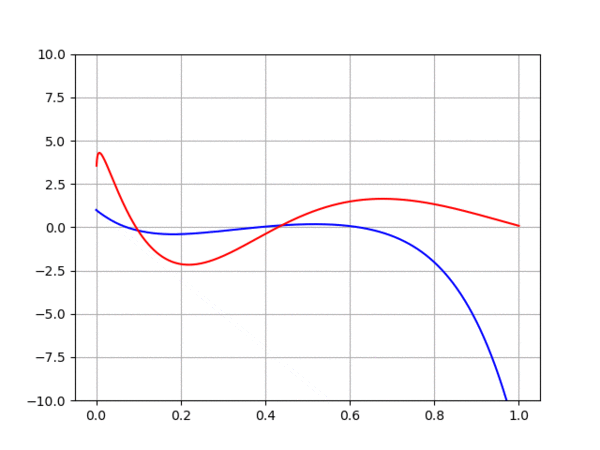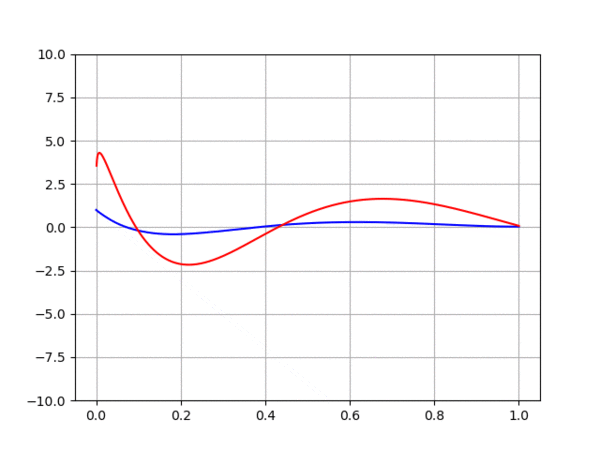Essai d'approximation par homotopie

Cas n°4

On considère une vague sphérique générée par une source périodique sinusoïdale.

Nous traitons ici de l'évolution de la surface libre dans un domaine infini en grande profondeur. La source ponctuelle est appliquée autour d'un cercle de rayon r_0 centré sur un domaine circulaire de rayon R qui laisse sortir librement cette onde en r=R.

L'équation de Berkhoff se simplifie alors en équation de Helmholtz et s'exprime en coordonnées polaires avec les conditions suivantes:

$ \begin{cases} \Delta \phi + k^2\phi=0, \\ \phi(r-r_0)=1, \\\phi_r(r=R)=ik\phi(r=R). \end{cases} $

En coordonnées polaires, la relation ci-dessus s'écrit de manière simplifiée étant donné que le problème est caractérisé par une symétrie de révolution, donc est indépendant de $ \theta $.

$  \begin{cases} \phi_{rr}+\dfrac{1}{r}\phi_r + k^2\phi=0, \\ \phi^{r=r_0}=1,   \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases}  $

• Résolution analytique

La solution de cette équation est de la forme $ \phi(r) = K_1 J_0(kr) + K_2 Y_0(kr) $

Avec les conditions initiales on a :

$ \phi (r=r_0) = K_1 J_0^{0} + K_2 Y_0^{0} = 1 $ avec $ J_0^{0} = J_0(kr_0) $ et $ Y_0^{0} = Y_0(kr_0) $

$ \phi_r(r) = k(K_1 J_1^r + K_2 Y_1^r) $ avec $ J_1^r= J_0' (kr) $ et $ Y_1^r =Y_0'(kr) $

$ \Rightarrow \phi_r(R) = k(K_1 J_1^R + K_2 Y_1^R) = ik (K_1 J_0^R+ K_2 Y_0^R) $

d'où

$ K_1 = \dfrac{Y_1^R -iY_0^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)} $

et

$ K_2 = \dfrac {iJ_0^R - J_1^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)} $

donc

$ \phi(r) = \dfrac{Y_1^R -iY_0^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)}J_0(kr) + \dfrac {iJ_0^R - J_1^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)} Y_0(kr)  $

• Résolution par homotopie

En coordonnées polaires, la relation d'homologie devient : $ (1-p) \phi_{rr} + p(\phi_{rr}+ \dfrac{1}{r} \phi_r + k^2\phi) = 0 $

En décomposant en série entière $ \phi(r) $, $ \phi_r(r) $ et $ \phi_{rr}(r) $ on obtient :

$ (1-p) [\phi_{0,rr} + p\phi_{1,rr} +p^2\phi_{2,rr} + ...] + p[\phi_{0,rr} + p\phi_{1,rr} +p^2\phi_{2,rr} + ...+ \dfrac{1}{r} (\phi_{0,r} +p\phi_{1,r} + p^2\phi_{2,r}+...) + k^2(\phi_0 + p\phi_1 +p^2\phi_2+...)] $

• • Ordre 0  :

$ \phi_{0,rr} (r) = 0 \Rightarrow \phi_0(r)= Ar +B $

Avec les conditions initiales :

$ \phi_0(r_0) = Ar_0 + B =1 \Rightarrow B=1-Ar_0 $

et

$ \phi_{0,r}(R) = ik\phi_0(R) \Rightarrow A = ik(AR+B) $

d'où

$ A = \dfrac{ik}{1+ik(r_0-R)} $

et

$ B = 1 - \dfrac{ikr_0}{1+ik(r_0-R)} $

donc

$  \phi_0(r) =\dfrac{ik}{1+ik(r_0-R)}r +1 - \dfrac{ikr_0}{1+ik(r_0-R)}  $ 

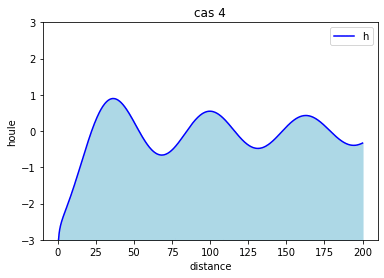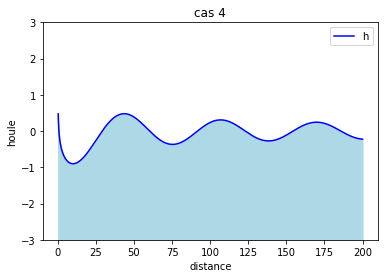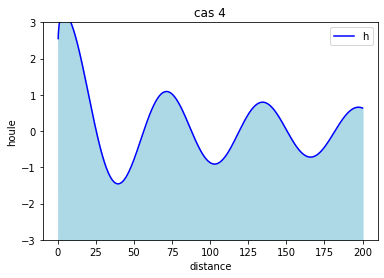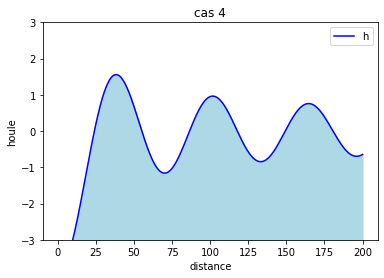
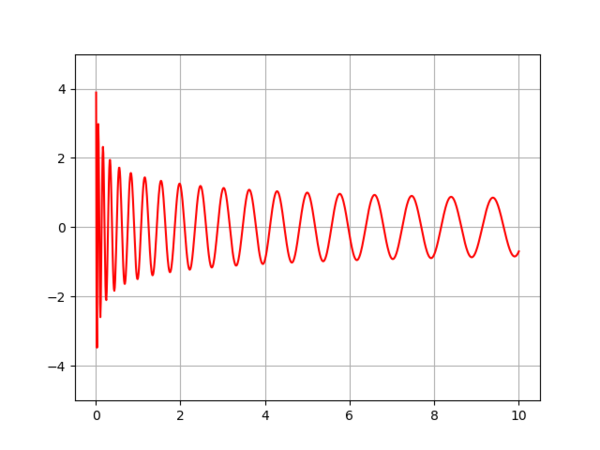
On constate qu'à partir de l'ordre 10 de l'ordre 10 la courbe gagne seulement en amplitude.

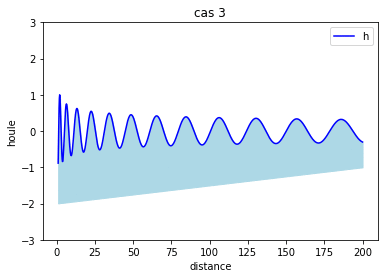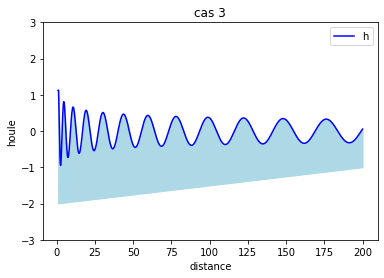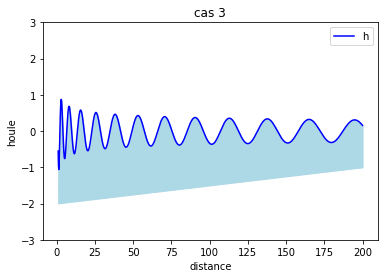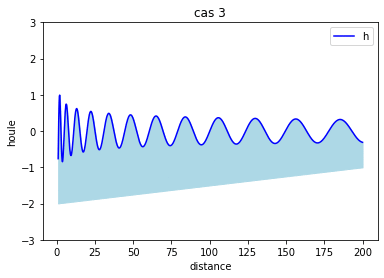
Cette courbe montre la hauteur en fonction de la distance mais pour différent temps. Le temps va de 0 à 10s.

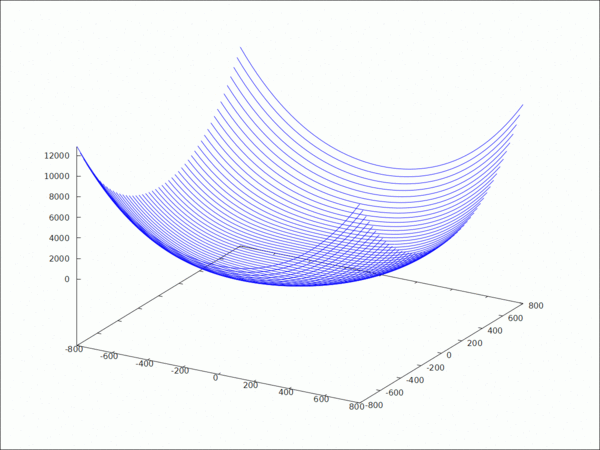
Modélisation finale en 3D du cas n°4

Analyse des résultats, limites et intérêts de la méthode d'homotopie

La méthode par homotopie nous a permis de gérer des équations non-linéaires et de faire varier les conditions aux limites. Elle offre une approche efficace pour représenter les caractéristiques complexes de la houle, ce qui est essentiel pour la gestion des risques côtiers et la conception des infrastructures maritimes. Améliorer le modèle de houle nécessiterait l'intégration de données en temps réel pour des prévisions plus précises.

Mais le logiciel maxima a des limites et certains paramètres comme les longueurs des canaux ou le nombre d'onde on été choisi pour alléger les calculs.

Cette méthode de modélisation reste néanmoins performante pour anticiper le comportement de la houle et prévoir des infrastructures adaptées pour limiter l'érosion ou les submersions.