Wikibardig:Barrage voûtes
Sommaire |
Barrage voûtes
Un barrage voûte reporte la majeure partie de la poussée de l'eau sur les rives par des effets d'arc.[...] La stabilité de ce genre d'ouvrage diffère essentiellement de celle des barrages poids, qui résulte d'une certaine inégalité entre la poussée de l'eau et le poids. Si l'eau monte, si la poussée augmente, un barrage poids glisse sur le sol ou même culbute lorsque l'équilibre statique vient à manquer. Ici au contraire, les réactions d'appui croissent en raison directe de la poussée de l'eau. Plus elle augmente, plus fortement elle applique l'ouvrage contre le sol, comme dans une fermeture autoclave. Pas de glissade ou de culbute possible, à condition que les rives tiennent bon. André Coyne (cours à l’ENPC en 1943)
Le principe d’un barrage voûte est donc de reporter la majeure partie de la poussée de l’eau sur les rives par des effets d’arc. Plus la poussée de l’eau augmente, plus elle plaque l’ouvrage contre les appuis. La construction de ces barrages conduit à une économie substantielle des volumes de béton mis en œuvre par rapport à un barrage poids. Si des constructions de voûtes sont connues à l’époque romaine, le premier barrage voûte de France est le barrage ZOLA conçu et construit par François Zola (père du célèbre écrivain Emile). Il permettait l’alimentation en eau potable de la ville d’Aix en Provence. D’une hauteur de 36 m, son épaisseur varie de 6 m en crête et 12,75m à la base. Son rayon de courbure est de 48,20m.
 |

|
| Barrage de ZOLA Parement aval Photo INRAE | Barrage de ZOLA Parement amont Photo INRAE |
Quatre conditions sont nécessaires pour envisager la construction d’un barrage voûte :
- Topographie : la vallée doit être étroite, la construction d’une voûte est intéressante si le rapport largeur en crête sur hauteur est inférieur à 5 ou 6 ;
- Rigidité de la fondation : pour que le fonctionnement « en voûte » soit possible, il faut que la rigidité de la fondation soit suffisante, sinon les arcs ne trouvent pas leurs appuis et la structure tend à fonctionner en console. En première approche, une voûte ne doit pas être envisagée, sans étude détaillées lorsque le module de déformation du rocher (mesuré par essais au vérin ou petite sismique) est inférieur à 4 ou 5 GPa. Lorsque sur l’un des appuis, la forme de la vallée est un peu fuyante, la voûte s’appuiera sur une culée en béton poids ;
- Résistance mécanique de la fondation : la voûte transmet des contraintes élevées à la fondation qui doit rester dans le domaine élastique pour ces niveaux de sollicitation ;
- Tenue des dièdres de fondation sous l’effet des sous pressions et compte tenu de la compression apportée par la voûte qui peut empêcher leur dissipation.
La stabilité des voûtes dépend essentiellement de la capacité des appuis rocheux à supporter des efforts relativement concentrés, dus à la poussée des arcs et à l'encastrement de la structure. Le barrage voûte exige une vallée étroite et un rocher de très bonne qualité mécanique.
Calcul des contraintes -Justification
« Formule du tube »
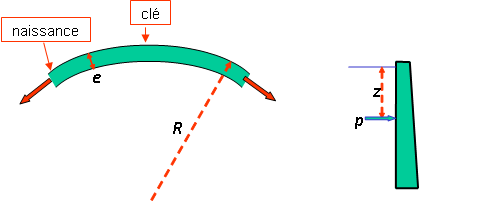
Coupe horizontale et section schématiques d’une voûte
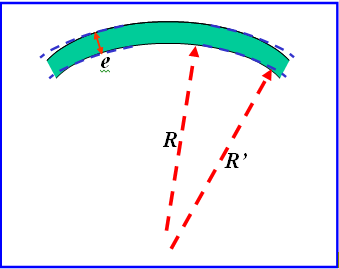
En première approximation, la contrainte dans les sections verticales situées à une section z, se calcule par la « formule du tube » en considérant la voûte comme un empilement d’arcs horizontaux indépendants : σ = p.R/e avec P=δw.Z (figure ci-dessus). Elle est uniforme dans tout l’arc supposé circulaire.
La contrainte admissible pour le béton, utilisée dans cette méthode simplifiée est de l’ordre de 4 à 5 MPa. (Pour un calcul complet en analyse élastique, on peut prendre des contraintes admissibles de 8 MPa en compression et de 1 MPa en traction).
Il résulte de la formule ci-dessus, que si tous les arcs ont la même courbure (R = constante avec z), alors l’épaisseur e à donner à l’arc varie linéairement avec la profondeur z. Si le parement amont est vertical, le parement aval est alors rectiligne avec un léger fruit.
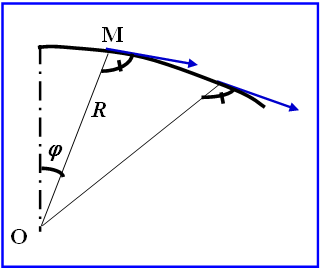
Angle au centre d’une voûte
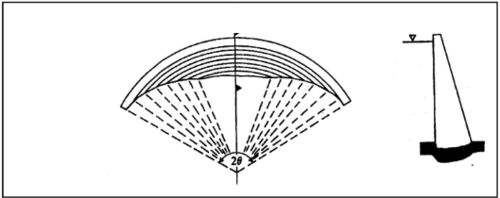
La formule du tube à elle seule laisse le choix entre une infinité de couples R et e. Un grand rayon diminue la longueur de la voûte mais oblige à l’épaissir. Un rayon plus faible permet de mincir la voûte, mais conduit à un moins bon arc-boutement de la voûte (appuis trop fuyants). Jorgensen a démontré en 1915 que l’angle au centre optimal, au plan économique, vaut 133,57°. En pratique, on adopte des angles compris entre 100 et 110°.
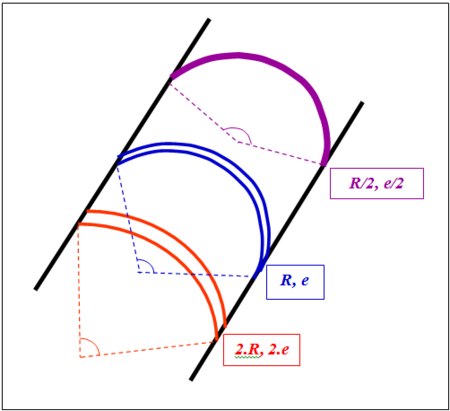
La voûte du centre est supposée optimale.La variante du haut est plus mince, mais mal appuyée.Celle du bas est bien appuyée mais trop épaisse.
Trial Load
Afin de tenir compte des liaisons entre les arcs successifs, on considère que le barrage est constitué de deux séries d’éléments : des poutres courbes horizontales (les arcs) et verticales (les consoles) qui se répartissent la poussée de la retenue, ainsi que les autres charges. La charge appliquée en chaque nœud par la retenue est répartie entre les deux familles de poutres, et les déplacements des arcs et des consoles doivent être égaux à leurs intersections. Deux des méthodes qui font appel à ce double découpage sont l’ajustement radial en clé (une seule console verticale) et la Trial Load dans laquelle le maillage est plus complet.
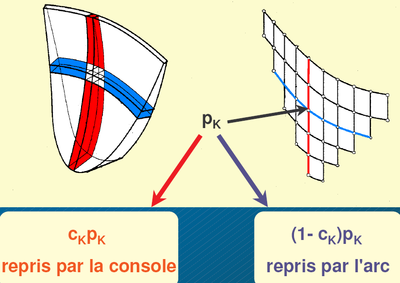
« Trial load » détermination de la répartition arcs / consoles des pressions hydrostatiques.(BETCGB)
Calculs aux éléments finis d’une structure, en statique ou en dynamique
La voûte et sa fondation sont découpées en volumes élémentaires, de type tétraèdres, hexaèdres ou octaèdres. Dans l’épaisseur de la voûte, on peut placer un ou plusieurs éléments. Ils sont étudiés séparément, puis assemblés par les « nœuds », points où sont appliquées les forces extérieures à l’élément.
Le calcul le plus classique utilise la loi de l’élasticité linéaire. On affecte un module d’élasticité à chaque élément, soumis à un effort tranchant et à un moment. Il est possible d’utiliser des modèles non linéaires, en simulant les joints (entre plots ; entre reprises de bétonnage) par des « éléments joints » qui obéissent par exemple au modèle de Mohr Coulomb et annulent les contraintes de traction.
Les inconnues du calcul sont les déplacements de chaque nœud. Le résultat d’un calcul, pour un cas de charge donné, donne les déplacements (ou les déformées) ainsi que les contraintes. On peut ensuite affiner la forme projetée, pour, par exemple, supprimer les zones où apparaissent des tractions en calcul linéaire.
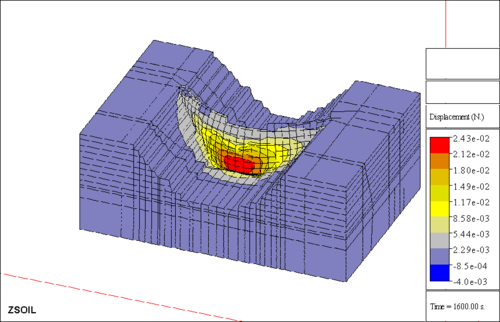
Exemple de représentation du calcul d’une structure par éléments finis
Forme de la voûte
Les barrages voûtes peuvent être répartis en 3 catégories selon la forme de la voute :
- Voûte à rayon constant ;
- Voûte à angle constant ;
- Voûte à double courbure ;
Les barrages poids-voûtes sont une autre catégorie des barrages voûtes. Ils peuvent aussi être considérés aussi comme des barrages poids. Ils font l’objet d’un chapitre particulier.
Voûtes à rayon constant
La voûte à rayon (amont) constant (figure ci-dessous) a un parement amont cylindrique à axe vertical ; l’angle d’ouverture décroît de la crête vers la base de la vallée, mais il ne faut pas qu’il décroisse trop. Ce type convient donc bien à une vallée en forme de U. C’est l’ouvrage le plus simple à concevoir et à réaliser. Pour des petits barrages, la simplicité conduit à choisir une épaisseur constante, et les deux parements sont donc verticaux (Les Cambous et Le Passet). Pour des barrages plus importants, l’épaisseur diminue du bas vers le haut le parement aval a donc un fruit. L’épaisseur peut aussi décroître, puis être constante comme au barrage de la Roucarié.
Voûte à simple courbure et à rayon constant
 |

|
| Les Cambous _Photo INRAE G2DR | Le Passet(66) Photo P. Royet- INRAE G2DR |

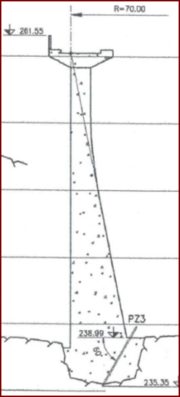
Voûte de la Roucarié (81) à simple courbure, à rayon constant, à parement aval incliné à la base et vertical au sommet. H = 26 m,.Photo INRAE- Source de la coupe : Coyne et Bellier
Voûtes à angle constant
Tous les arcs d’une voûte à angle constant (figure ci-dessous) ont le même angle d’ouverture (en général de 100 à 130°) ; le rayon de courbure diminue depuis la crête vers le fond de vallée ; les sections droites du centre de la vallée ont obligatoirement un surplomb vers l’aval ; les sections proches des appuis ont un surplomb vers l’amont (qui ne doit pas être excessif). Cet ouvrage est plus complexe mais plus économique en volume de béton. Il convient bien à une vallée en forme de V.

Voûte à arcs horizontaux et à angle constant
Voûtes à double courbure
Principe de la voûte à double courbure
Dans une voûte de type quelconque, les arcs se déforment radialement (en plan) de façon différente selon la profondeur. Un arc long tend à se déplacer plus qu’un arc court, ce qui induit un cisaillement entre arcs horizontaux et incline les contraintes qui « plongent » vers les rives. On parle d’arc plongeant (figure ci-dessous, gauche). La poussée de l’eau en chaque point du parement amont se répartit entre :
- une force reprise par les consoles verticales ; comme les barrages poids, ces consoles, sous l’effet de cette part de poussée, génèrent des efforts tranchants et des moments de flexion entre les arcs ;
- une force reprise par les arcs ; le cisaillement entre arcs horizontaux, et le plongement des contraintes qui en résulte tend à soulever les consoles du centre.
En supposant les arcs indépendants :
- dans la partie supérieure, les poussées sont faibles et la flèche de l’arc le plus haut est quasiment nulle ;
- plus en profondeur, les flèches augmentent puis diminuent en approchant de la base, du fait de la diminution de longueur de l’arc (figure ci-dessous, droite).
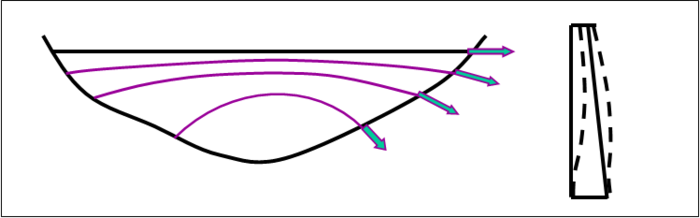
Arcs plongeants et déformée de la section droite d’une voûte de type quelconque.
Mais en réalité l’hyperstatisme implique :
- qu’en partie haute, les arcs sont chargés par les consoles et se déforment davantage ;
- qu’en partie basse, les arcs se déchargent sur les consoles et de déforment moins.
La double courbure utilise à son profit cet effet de console. En partie basse, là où les arcs chargent les consoles, on diminue la tendance néfaste à la flexion en donnant du poids déporté à l’amont. La partie basse des consoles a donc un fruit aval. On peut parler d’une véritable précontrainte permise par ce surcroît de poids amont, qui diminuera l’ouverture du joint amont lors de la mise en eau. En partie haute, là où les consoles chargent les arcs, ce qui est bon pour la sollicitation des appuis, on incline encore plus les réactions d’appui en donnant aux consoles un fruit amont. Au total, la console a donc la forme d’un arc dans le sens vertical (figure et photos ci-dessous).
La double courbure permet de réduire les rayons des arcs inférieurs, les plus chargés. Elle réduit les cisaillements horizontaux en pied des consoles centrales. Elle limite l’ouverture du joint amont.
Dans les barrages à double courbure, le rayon des faces amont et aval est variable, aussi bien horizontalement que verticalement. Ce type de profil permet de réduire significativement l’épaisseur de la voûte et le volume de béton mis en œuvre.

Schéma d'une voûte à double courbure

Voûte à double courbure du barrage de Bimont H=87 m Photo INRAE-G2DR
Conception des voutes à double courbures
Intérêt de la courbure variable (en plan)
Les arcs d’un barrage voûte sont moins chargés par les consoles aux naissances qu’à la clé, car les consoles y sont plus courtes. Cela autorise donc à augmenter les rayons de courbure près des naissances. La forme idéale est une spirale logarithmique, courbe d’équation polaire $ R=a.e^{K.\varphi} $, où $ \varphi $ est l’angle par rapport à l’axe de la vallée.
En fonction de la hauteur H de la voûte et de deux largeurs de vallée, L1 au sommet et L2 proche de la base, les formules USBR (United States Bureau of Reclamation) donnent la forme de la console de clé de la voûte :
ec = 0,01.(H + 1,2.L1)
eb = $ \sqrt[3]{(0,0012.H.L_1.L_2.(0,008202.H)^{0,008202.H}} $
em = 0,9.eb
Dessin de la section d’une voûte
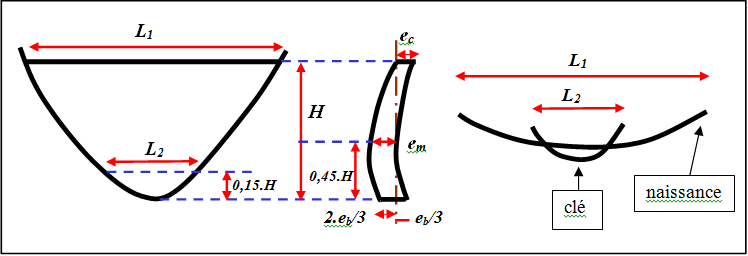
Dimensions caractéristiques d’une voûte à double courbure, selon l’USBR (vues en coupe rive à rive, en section amont-aval et en plan)
La forme en plan des deux parements peut être donnée par leur équation polaire. On trouvera ci-après l’équation des deux parements du barrage d’Esch sur Sûre au Luxembourg, conçu par COB et haut de 50 m (z est la cote du plan considéré mesuré sous les PHE, $ \varphi $ l’angle du rayon considéré par rapport à l’axe du barrage) :
Ramont = $ 81,118+8,075\frac{z}{42} - 2,975\left(\frac{z}{42} \right)^2 -32,7666(1-cos\varphi)^2 \left(\frac{z}{42} \right)^2 $
Raval = $ 79,618+6,093\frac{z}{42} - 3,680\left(\frac{z}{42} \right)^2 -51,406(1-cos\varphi)^2 \left(\frac{z}{42} \right)^2 $
On constate que le rayon augmente légèrement de la clé vers les naissances (du fait du cos$ \varphi $). La largeur en crête est égale à 1,5 m (différence des rayons pour z=0). Dans d’autres cas, le polynôme en z est du 3ème degré (comme pour la voûte de Kariba sur le Zambèze achevée en 1958, haute de 128 m sur fondation et qui crée le plus grand lac artificiel au Monde : 181 km3).
Les barrages poids-voûtes
Les barrages poids-voûte sont en fait des barrages poids. Ils ont une forme légèrement arquée qui autorise un report partiel de contraintes sur les appuis latéraux Ce type de barrage convient bien dans une vallée modérément large dont le rocher n’a pas la qualité suffisante pour reprendre totalement les poussées. Les premiers poids-voûte datent de la fin du XIXe siècle, en Angleterre et en France, où l’on cherchait surtout, grâce à la forme voûte, à refermer les fissures amont et à empêcher ainsi le développement des sous-pressions dans le corps du barrage.


Barrages poids voûte en maçonnerie de la Bourne (26) construit en 1870, haut de 18 m sur la fondation et de Saint- Martin de Londres (34) construit en 1923. Photos INRAE - G2DR
Pathologies affectant les barrages voûtes
Des pathologies peuvent affecter la fondation ou le corps de l’ouvrage. Elles sont identiques à celles rencontrées sur les barrages poids béton.
- Fondation de l’ouvrage :
- Erosion et dissolution
- Vieillissement des rideaux d'injection et des réseaux de drainage;
- Corps de l’ouvrage :
- Réaction chimique conduisant au gonflement interne : l'alcali-réaction
Construction barrages voûtes
Les barrages-voûtes sont construits par plots verticaux indépendants (photos ci-dessous). Ces plots joueront le rôle de console lorsque la mise en eau sera effectuée. En fin de construction, les plots sont clavés de manière à rendre la voûte monolithique et à solliciter lors de la mise en eau, à la fois les arcs horizontaux et les consoles verticales.

Construction du barrage de Bimont(13) (photos : Société du Canal de Provence)
Qualités requises et traitement de la fondation
La construction d’un barrage voûte nécessite des fondations d’excellentes qualité mécanique. Elles doivent résister aux sollicitations induites par l’ouvrage lui-même et par l’eau stockée dans la retenue. Les études et reconnaissances géotechniques doivent être très complètes et comprennent toujours une analyse géologique qui permettra d’identifier, a priori, Les zones de discontinuité (failles, joints, diaclases).
On procèdera, ensuite, à des essais mécaniques : sondages de reconnaissances, galeries creusées dans les rives, essais de laboratoire, essais in situ (mesure de la déformabilité par chargement direct, résistance à la compression, au cisaillement) ;
Des mesures indirectes (géophysique, petite sismique) permettrons de comparer différents de sites de voûtes entre eux.
Les calculs seront effectués sur une surface d’appui fictive purgée de la partie superficielle des appuis (rive) qui est toujours de moindre qualité. Ils permettront de vérifier que les forces exercées par le barrage lui-même et les forces exercées par les pressions d’eau dans les appuis ne peuvent pas déstabiliser les rives ou une partie de celles-ci. La poussée de la voûte est peu déstabilisatrice en elle-même, à condition que les arcs ne fassent pas un angle trop aigu avec la courbe de niveau correspondante (30° est une valeur minimale). Le risque principal pour la stabilité de l’ouvrage est les sollicitations exercées par les pressions de l’eau de la retenue dans la fondation. Pour limiter ces sollicitations, tous les appuis de barrages voûtes sont maintenant équipés de systèmes drainages abondants, visités, entretenus et auscultés.
La vérification de la stabilité des rives doit être vérifiée. Pour cela, on peut utiliser la méthode dite des coins rocheux (Londe ,1973).

Étude de la stabilité d’une rive (méthode des coins - Londe) O, A, B, C =Tétraèdre ; P1, P2, P3 = Surfaces de séparation géologiques ; U1, U2, U3 = Forces dues à la pression de l’eau ; W = Poids de l’eau ; Q= Poussée du barrage
Sous l’action des différentes forces, le coin à tendance à glisser vers le vide. On vérifie, par le calcul la valeur de l’angle de frottement au niveau des surfaces de contact (P), nécessaire pour assurer la stabilité du coin rocheux et on compare cette valeur à la valeur de l’angle de frottement résiduel de la roche.
Rupture d’un Barrage voûte
Il y a eu une seule véritable rupture de barrage voûte dans le Monde, celle du barrage français de Malpasset. Rupture du non à la voûte elle-même, mais à la défaillance en profondeur d’une rive, dans des conditions de structure géologique, de pétrographie et dépressions interstitielles très particulières (qui n’étaient d’ailleurs pas envisageables dans l’état des connaissances de l’époque). Cette rareté s’explique par la grande sécurité de ce type de barrage vis-à-vis de la poussée de l’eau, pourvu que les appuis tiennent bon. La catastrophe du barrage italien de Vajont en 1963 illustre bien cette résistance, puisque une vague de 100 m a résulté d’un grand glissement de terrain dans la retenue. Elle a provoqué un très grand nombre de victimes, sans pour autant rompre le barrage.
Rappel des liens accessibles sur cette page :
|
Références
BETCGB (Bureau d’Étude Technique et de Contrôle des Grands Barrages), 2016 - Formation « Barrages en béton » - La modélisation des barrages voûtes.
Carrere A., 1994. Barrages. Techniques de l’ingénieur, traité de construction.
Carrere, A., 2001. Conception des barrages voûtes, exposé au colloque technique du CFBR (Comité français des barrages et réservoirs), Aix-en-Provence, 26 p.
CFBR (Comité Français des Grands Barrages), 2002. Petits barrages : recommandations pour la conception, la réalisation et le suivi. Coordination Gérard Degoutte. Cemagref Editions-2° édition.
CFBR (Comité Français des Grands Barrages), 2018. Recommandations pour la justification du comportement des barrages voûtes ISBN: 979-10-96371-07-5 – dépôt légal 4ème trimestre 2018.
CIGB (Commission Internationale des Grands Barrages), 1994. - Bulletin 93 - Vieillissement des barrages et des ouvrages annexes.
Degoutte G., Mercklé S., 2012. Cours de l’ISBA (Institut Supérieur du Béton Armé) - Chapitre 6 – Barrages voûtes et barrages à contreforts.
James, P., Chanson, H., 2004. Une histoire révisée des barrages voûte, des barrages romains aux ouvrages modernes en béton, Australian Civil Engineering Transactions, pp 39-56 (en anglais).
Jorgensen, L.R., 1915. The Constant-Angle Arch Dam, Transactions, ASCE, Vol. LXXVIII, pp. 685-721. Discussion : Vol. LXXVIII, pp. 722-733.
Mercklé S., 2012. Cours ENGEES (École Nationale du Génie de l'Eau et de l'Environnement de Strasbourg) – Dimensionnement et construction barrages en béton.
Peyras, L. - 2003. Diagnostic et analyse de risques liés au vieillissement des barrages, développement de méthodes d'aide à l'expertise. Doctorat spécialité Génie civil, école doctorale des sciences pour l'ingénieur, laboratoire d'études et de recherches en mécanique des structures (LERMES), Université Blaise Pascal, Clermont II. 254 p.
USBR, (United States, department of the interior, bureau of reclamation), 1987. Design of small dams, Denver Colorado, 1987. Third edition, 860 p.
![]() Pour revenir au menu « Visite guidée »
Pour revenir au menu « Visite guidée »
Pour plus d'information sur l'auteur : INRAE - UMR RECOVER - Equipe G2DR
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS