Wikibardig:Survey
Sommaire |
PRINCIPE DE L'ANALYSE STATISTIQUE PAR LE LOGICIEL SURVEY
Le modèle statistique
La méthode la plus simple pour la surveillance d'un phénomène observé sur un ouvrage peut consister à en considérer les mesures brutes, en les portant par exemple sur un graphique en fonction du temps. Ce procédé apporte peu de renseignements relatifs au comportement de l'ouvrage face aux diverses sollicitations. Quant à l'évolution du phénomène dans le temps, elle n'est suggérée qu'au milieu d'un nuage de points fortement dispersés par les sollicitations.
Afin d'obtenir des grandeurs comparables entre elles, les mesures brutes sont ramenées à un état de sollicitation de référence, c'est à dire à des conditions identiques de sollicitations. On peut alors quantifier les évolutions irréversibles (temporelles) de l'ouvrage.
Le logiciel “SURVEY” de IRSTEA est un programme informatique de gestion et de traitement statistique des données d'auscultation des barrages. Ce traitement consiste à ajuster les mesures “brutes” d'auscultation “y” à un modèle explicatif “Yc”.
Les variables physiques à expliquer correspondent aux mesures in situ : déplacements, déformations, niveaux piézométriques, pressions, débits de fuite, …
Les variables physiques explicatives de ces mesures sont, dans le cas des barrages :
- - la cote du plan d'eau, dont l'effet est noté “H”;
- - la date dans l'année, dont l'effet saisonnier inter-annuel est noté “S”;
- - le temps (ou l'âge du barrage), dont l'effet irréversible est noté “T”.
Le modèle explicatif utilisé est basé sur le modèle “HST” proposé par EDF, formulé à l'origine pour les barrages voûtes en béton.
Le modèle développé à Irstea prend en compte une variable explicative supplémentaire :
- - la pluie, dont l'effet est noté “P”
Il comporte 18 paramètres. La valeur calculée Yc est décomposée comme
Yc(t) = Y0+H(t)+S(t)+T(t)+P(t)
où Y0 est un paramètre.
La méthode d'ajustement est une régression linéaire multiple : ces 18 paramètres sont estimés par moindres carrés. Une méthode pas à pas “Stepwise” permet de sélectionner les paramètres les plus significatifs. Elle est basée sur les tests de Fischer-Snédecor et de Student.
Le résidu $ \varepsilon $(t) est défini par l'écart entre la mesure y(t) et la valeur calculée Y C (t) :
$ \varepsilon(t)=y(t)-y_c(t) $
Effet "H" dû à la retenue
L'effet hydrostatique H(t) nécessite de connaître l'historique de la cote du plan d'eau Z(t). Il est représenté comme fonction polynômiale (4 paramètres) de la côte centrée réduite du plan d'eau sur la période d'analyse [ti,tf] :
$ H=a_1Z+a_2Z^2+a_3Z^3+a_4Z4 , Z(t)= \frac{Z(t)-Z}{\sigma(Z)} $
Le graphique “analyse de la variation du plan d'eau” contient la valeur calculée H(Z) en fonction de la cote de la retenue Z (traits pointillés), et les valeurs des mesures brutes corrigées des autres effets(saisonnier, temps et pluie) : y-(S+T+P) (points), c'est à dire $ H(Z)+ \varepsilon $.
On associe à cet effet le coefficient ”$ \alpha $”, qui est le facteur d'amortissement (égal à $ a_1/ \sigma(z) $ dans la plupart des cas, lorsque l'effet est linéaire): $ \alpha=\frac{amplitude\ des\ variations\ de\ la\ mesure}{amplitude\ des\ variations\ de \la\ cote\ du\ plan\ d'eau} $
Effet saisonnier "S" dû à la date dans l'année
Afin de rendre compte des dissymétries des cycles saisonniers, l'effet saisonnier S(t) est représenté par la somme de fonctions sinusoïdales de période un an et six mois, et de phase inconnue (Ce sont en fait les deux premiers termes d'un développement de Fournier) . Il s'écrit en fonction de “l'angle saisonnier” θ(t) (jour dans l'année, à 2π près) :
S(t)=b1sin(θ)+b2cos(θ)+b3sin2(θ)+b4sin(θ)cos(θ) , θ(t)=$ \frac{2{\pi}t}{365.25} $
Les effets saisonniers sont bien connus sur les barrages voûtes. Ils correspondent à l'influence des écarts de températures entre les saisons froides et les saisons chaudes. Ces écarts mesurés sont étroitement corrélés aux déplacements ou aux déformations.
Pour les barrages en terre destinés à l'alimentation en eau ou à l'irrigation, cet effet est également constaté, mais beaucoup plus difficile à interpréter physiquement compte-tenu de la gestion essentiellement saisonnière de ces retenues. On peut la plupart du temps l'imputer à la retenue : il en représente alors la composante saisonnière. L'effet de la retenue sur les variations de mesures peut comporter un retard, qui n'est pas pris en compte dans le modèle : l'interprétation doit en tenir compte.
Le graphique analyse saisonnière” contient la valeur calculée S(θ) en fonction de la date dans l'année θ (traits pointillés), et les valeurs des mesures brutes corrigées des autres effets (retenu, temps et pluie) : y-(H+T+P) (points), c'est à dire S(θ)+ε.
Effet du temps "T" dû à l'âge de l'ouvrage
Les effets irréversibles T(t) sont représentés par la somme d'un terme linéaire en temps, d'une exponentielle positive (évolution accélérée) et d'une exponentielle négative (évolution amortie) en fonction du temps réduit $ {\tau} $(t)sur [ti,tf] :
T(t) = C1$ {\tau} $+C2e$ {\tau} $+C3e$ -{\tau} $ ,
$ {\tau} $(t)=$ \frac{t-t_i}{t_f-t_i} $
Le graphique “analyse à conditions constantes” contient la valeur calculée T en fonction du temps réduit $ {\tau} $(traits pointillés), et les valeurs des mesures brutes corrigées des autres effets (retenue, saison et pluie) : y-(H+S+P) (points), c'est à dire T($ {\tau} $)+ε
On associe à cet effet la vitesse moyenne d'évolution “v” sur la période d'analyse :
$ V=\frac{amplitude\ d'evolution\ de\ la\ mesure}{duree\ de\ cette\ evolution} $
Effet "P" dû à la pluie
L'effet pluviométrique est ici modélisé à l'aide des variables pk(t), qui sont les moyennes sur sept jours des pluies antérieures de k semaines à t (fig 1) :
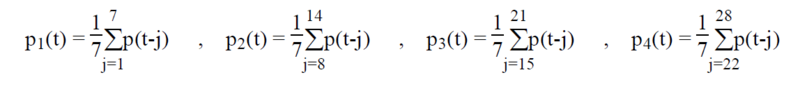
Les moyennes sur quatorze jours des pluies antérieures de cinq et sept semaines sont également prises en compte par les variables p56(t) et p78(t) (fig 1) :
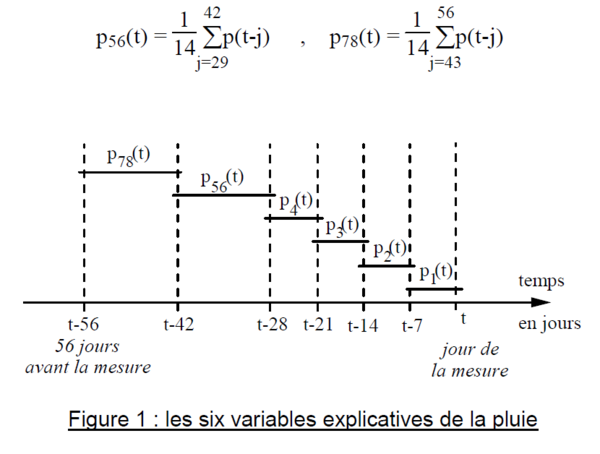
Les effets de la pluviométrie P(t) sont alors représentés par une fonction linéaire de ces six variables :
P(t) = d1p1(t) + d2p2(t) + d3p3(t) + d4p4(t) + d5p56(t) + d6p78(t)
Le graphique “effet pluviométrique” contient la valeur calculée P en fonction de la date t (traits pointillés), et les valeurs des mesures brutes corrigées des autres effets (retenue, saison et temps) : y- (H+S+T) (points), c'est à dire P(t)+ε
En pratique, c'est la pluie tombée les quelques jours précédent la mesure qui est influente : dans la plupart des cas, seul le paramètre p1 est significatif.
Evaluation de la qualité d'une analyse
Le coefficient global de détermination R2 caractérise le rapport entre les variations expliquées par le modèle et les variations totales des mesures faites sur les instruments :
$ R^2=\frac{variance\ expliquee}{variance\ totale}= 1 - \frac{variance\ resuduelle}{variance\ totale} $
Ce coefficient R2 est compris entre 0 et 1. Plus R2 est proche de 1, meilleure est l'adéquation. En pratique, une analyse est insignifiante lorsque R2 <0,35, et excellente lorsque R2 >0,81.
Ce coefficient, robuste, peut être sensible aux points extrêmes, et l'analyse visuelle des graphiques est indispensable pour juger de la qualité des résultats, et les interpréter au mieux.
Les lacunes potentielles sont de plusieurs ordres :
- effets des variations extrêmes des phénomènes expliqués (par construction, les effets saisonniers modélisés sont des effets “moyens”);
- effets des variations dues à des phénomènes non pris en compte par le modèle (effet “retard” : influence déphasée de la retenue ou de la pluie, influence d'un écoulement venant d'un versant,…);
- forte corrélation des variables explicatives du modèle : corrélation entre retenue, saison et pluie;
- mauvaise représentativité du nuage de mesures vis à vis des phénomènes modélisés : trop grande périodicité de mesure, présence de valeurs anormales;
- incertitudes liées à l'instrument de mesure lui-même, ou à la réalisation de la mesure (changement de mode opératoire, …).
Références
Bonelli S., Félix H., Tourment R. (1998). Interprétation des mesures d’auscultation des barrages par régression linéaire multiple ‘HST’. 2ème Conférence nationale JN-FIAB’98 sur la Fiabilité des Matériaux et des Structures. Marne-la-Vallée, France.
Pour plus d'information sur l'auteur : INRAE - UMR RECOVER - Equipe G2DR
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS