Wikibardig:Technologie des barrages poids
Sommaire |
Technologie des barrages poids
Cette rubrique présente les bases technologiques et fonctionnelles des barrages poids. Elle définit la typologie et les caractéristiques principales des barrages poids et détaille les principaux phénomènes agissants sur ceux-ci.
Caractéristiques générales
La typologie des barrages poids est établie à partir des matériaux les constituant. On distingue selon DEGOUTTE (1997) :
- les barrages poids en Béton Conventionnel Vibré (BCV) ;
- les barrages poids en Béton Compacté au Rouleau (BCR), mettant en œuvre un béton maigre (100 à 150 kg de ciment par m3 ) travaillé comme un matériau meuble.
Ils sont massifs (en comparaison avec les barrages en remblais) et résistent à la poussée de l’eau par leur poids. Etant donné les matériaux les constituants, ils sont considérés comme rigides et nécessitent donc des fondations rocheuses de bonnes qualités.
Les profils des barrages poids ont évolué avec le progrès de l’ingénieur et des matériaux. PEYRAS (2003) distingue :
- les profils arqués, employés pour les ouvrages en maçonnerie construits au XIXème siècle et donnant des ouvrages généralement minces ;
- les profils trapézoïdaux avec parements amonts verticaux, les plus classiques et correspondant aux ouvrages en BCV et BCR ou maçonnerie ;
- les profils symétriques, utilisés pour des ouvrages en BCR ou remblai dur construits sur des fondations de faibles caractéristiques mécaniques (rocher altéré, fondations alluviales) et permettant de limiter les sollicitations portées au sol.

Composants des barrages poids
Les parements ont pour principale fonction la protection du corps du barrage vis-à-vis des sollicitations extérieures. La pérennité de l’ouvrage dépend donc étroitement des qualités de la conception et de la réalisation. On distingue deux types de parement :
- parement amont : il constitue la surface de contact avec l’eau de la retenue. Pour remplir son rôle de protection, il doit être conçu pour résister aux actions agressives susceptibles de « contaminer » le corps du barrage. Il a pour principale fonction la protection du corps du barrage vis-à-vis des sollicitations extérieures et assure notamment une fonction d’étanchéité. Soumis aux sollicitations thermiques et hydrométriques engendrées en particulier par les variations de la cote du plan d’eau, le parement amont doit également résister aux sollicitations induites par les corps de flottants (tronc d’arbre, …) éventuels.
- parement aval : il constitue le versant aval du barrage. Il doit être conçu et réalisé pour assurer la protection du corps du barrage vis-à-vis des variations, souvent importantes, des conditions atmosphériques (vieillissement en surface dû aux cycles gel/dégel, à l’exposition au soleil, aux variations de températures, au vent, …) et du niveau du plan d’eau aval.
La crête est située au sommet du barrage. Elle agit contre l’infiltration des eaux de pluie dans le corps du barrage et permet, dans certains cas, le passage de véhicules ou de piétons.
Le système de drainage du corps du barrage est constitué de galeries et de conduites placées en aval du parement amont. Il a pour objet de réduire les sous-pressions dans le corps du barrage poids en drainant les eaux infiltrées. En général ce dispositif n’est pas mis en place pour les barrages de faible hauteur (moins de 15 mètres).
Le système d’étanchéité des fondations a pour fonction d’éviter à l’eau de pénétrer dans les fondations afin de limiter les sous-pressions. Il est principalement constitué d’injections dont le but est de créer un rideau étanche dans le rocher. Un coulis sous pression est injecté selon une ou plusieurs lignes afin d’étancher les chemins par où l’eau peut passer.
Le système de drainage des fondations est le complément indispensable des travaux d’injection. En effet, il a pour but d’évacuer rapidement les eaux d’infiltrations afin d’éviter qu’elles ne soient mises en pression, ce qui a pour conséquence d’augmenter les débits de fuites. Le système de drainage est normalement assuré par des forages (Ministère de l’agriculture, 1977).
Les tirants d’ancrage ont pour but d’augmenter le poids de l’ouvrage afin de le stabiliser. Le dispositif consiste à ancrer profondément le massif d’appui au moyen de câbles mis en tension. Pour cela on exécute un sondage de gros diamètre dans lequel on descend un câble métallique que l’on scelle à la partie inférieure, dans le terrain, par injection. La partie haute du tirant est prise dans un bloc de béton armé et fretté.

La figure ci-dessous résume l’ensemble des composants (et leur fonction), d’un ouvrage poids :

Stabilité des barrages poids
Cette partie propose d’identifier les principales actions intervenant dans les justifications de la stabilité des barrages poids et d’indiquer les principes généraux de leur calcul. Les recommandations qui en résultent émanent d’une synthèse des principales recommandations existantes et des pratiques de l’ingénierie française issues du CFBR (2012).
En fonction de leur variation au cours du temps et de leur intensité, les actions sont classées en trois catégories :
- les actions permanentes ;
- les actions variables ;
- les actions accidentelles.
Valeurs caractéristiques des actions permanentes
Les actions permanentes sont les actions continues ou pratiquement continues dont l’intensité est constante ou très peu variable dans le temps.Les actions permanentes sont notées G.
Poids propre G0
De façon générale, le calcul de l’intensité du poids propre des barrages en béton ou maçonnerie ne pose pas de difficulté particulière. Il est conduit à partir des dessins et des coupes du projet et en prenant compte de la surface du profil étudié (S), du poids volumique humide des matériaux du barrage $ (\gamma_b) $ et du poids des équipements fixes.Certaines sections particulières présentant des évidements pourront faire l’objet d’une justification distincte tenant compte d’un poids propre plus faible.

On adopte, pour la valeur caractéristique du poids propre, notée $ G_{0k} $, la formulation suivante :$ G_{0k}=\gamma_{b,k}.S $
a. Cas des barrages poids en béton Pour les ouvrages en béton, la valeur moyenne du poids propre des structures est connue avec une bonne précision et son coefficient de variation est faible. Généralement, on dispose d’essais abondants et l’utilisation des méthodes statistiques est alors possible, la valeur caractéristique du poids volumique sera une estimation prudente de la valeur moyenne du poids propre, cette dernière étant calculée à partir du poids volumique moyen des tests effectués.
b. Cas des barrages en maçonnerie
Pour les barrages en maçonnerie existants, le poids volumique humide des matériaux peut être sujet à fluctuation dans l’espace au sein de la structure et dans le temps sous l’effet de mécanismes de dissolution et d’érosion des mortiers. Dans ce cas, on ne peut pas retenir, pour la valeur caractéristique du poids propre, une valeur nominale basée sur la moyenne du poids volumique mesuré sur des carottes de sondages. En effet, les carottes intactes qui parviennent au laboratoire ne sont pas forcément représentatives de l’ensemble du corps de l’ouvrage.
Il est recommandé d’évaluer le poids volumique humide moyen du barrage en combinant plusieurs approches et, en particulier :
- la mesure du poids total des caisses de carottes prélevées en sondages ;
- le re-calcul du poids volumique moyen en évaluant la proportion relative des pierres, du mortier et des vides, et en pondérant chacune par leur densité. Proportion et densité peuvent être appréciées sur carottes, et dans certains cas en exploitant les documents de construction ;
- la mesure du poids volumique en forage au moyen d’une sonde à émission et réception de rayonnement gamma ; moyennant une calibration sur des mesures en laboratoire, on obtient un log de la densité de la maçonnerie tout au long du forage ; l’état de la pratique actuelle ne permet pas d’utiliser cette technique autrement qu’en complément des deux approches précédentes ;
- le jugement d'expert.
En première approche, dans le cadre d’un diagnostic rapide, on peut situer les valeurs moyennes du poids volumique humide de la maçonnerie dans une fourchette de 22 à 24 kN/m3. Toutefois, des valeurs moyennes plus faibles, inférieures à 20 kN/m3, ont été mesurées sur des barrages parmi les plus anciens [Royet, 2003] . Des reconnaissances approfondies par sondages sont donc recommandées, en veillant particulièrement à la représentativité des échantillons sur lesquels sont faits les essais de laboratoire.
Les poids volumiques faibles correspondent à des indices des vides plus importants que dans le béton : la différence entre les poids volumiques sec, humide et saturé devient significative. Il y a lieu d’en tenir compte dans l’analyse.
c. Cas des barrages-poids en béton à gros agrégats ou en béton cyclopéen
Nous pouvons établir la distinction suivante entre ces deux types de matériaux :
- le béton à gros agrégats est un béton conventionnel vibré dont la taille des plus gros agrégats dépasse largement celle des BCV classiques et va jusqu’à 120 mm ;
- le béton cyclopéen est un béton conventionnel dans lequel on déverse des enrochements ou des blocs.
Dans le premier cas, la détermination du poids propre se fait comme pour les barrages en béton classique, à la nuance près qu’il conviendra, sur les barrages existants, de veiller à la représentativité des carottes de sondage (diamètre des carottes par rapport à la taille maximale des agrégats). Pour les barrages en béton cyclopéen, la détermination du poids propre suit une logique équivalente à la démarche exposée ci-avant pour les ouvrages en maçonnerie en exploitant une longueur significative de sondages carottés. Dans un objectif d’appréciation correcte du poids volumique moyen du corps du barrage, une attention doit être portée à la potentielle hétérogénéité dans l’espace (en hauteur mais également en [x, y]) de ces paramètres, ainsi qu’à la prise en compte d’éventuels vides importants par défauts de remplissage.
Poussée des sédiments G1
Le principe du calcul de l’action des sédiments revient à un calcul de poussée. Les sédiments sont considérés non pas comme un fluide, mais comme un matériau pesant et frottant, défini donc par son poids volumique déjaugé γ’sédiment et son angle de frottement interne φ sédiment, et venant interagir comme un milieu extérieur au système « barrage » en y exerçant une action de poussée sur le parement amont.

En premier lieu, il convient de déterminer la hauteur du massif des sédiments. Pour les barrages neufs, elle fait partie intégrante des données du projet et est obtenue par des études spécifiques. La poussée des sédiments étant toujours défavorable vis-à-vis des états-limites à justifier, on estime une hauteur maximale des sédiments à moyen et long terme. Pour les barrages existants, elle est obtenue sans (trop de) difficulté en considérant les niveaux historiques de l’envasement de la retenue, et leur évolution.
Ensuite, le calcul est mené en contraintes effectives et on calcule la poussée des sédiments à partir du poids volumique déjaugé γ’sédiment.
Les difficultés résident dans la détermination de γ’sédiment et Kindice, et on trouve dans la littérature de nombreuses hypothèses sur ces paramètres. Plutôt que de raisonner sur chacun des deux paramètres considérés isolément, on propose de retenir une valeur globale égale au produit du coefficient de poussée par le poids volumique immergé des sédiments : K. γ’sédiment
A défaut d’informations plus précises, on recommande d’adopter en première approche la valeur caractéristique suivante, correspondant à une estimation experte prudente du paramètre K. γ’sédiment raisonnablement envisageable du côté des valeurs défavorables :
K. γ’sédiment = 4 kN/m3
Cette poussée vient en supplément de la poussée de l’eau.
Dans le cas d'un parement amont incliné, à la composante horizontale déterminée avec la valeur K.γ’sédiment définie ci-dessus, il convient de rajouter une composante verticale d'intensité γ’sédiment. Un ordre de grandeur pour γ’sédiment est de 12 kN/m3.
En situation sismique, certains sédiments sont susceptibles de se liquéfier, en particulier les sédiments fins à faible densité. Des études spécifiques sont nécessaires, en particulier la détermination des propriétés mécaniques de ces sédiments. Une première approche sécuritaire consiste à prendre un coefficient de poussée hydrostatique de 1, appliqué au poids volumique effectif des sédiments.
Poussée d’une recharge aval G2
Deux configurations sont à distinguer :
Cas d’un remblai de pied : La recharge aval est ici un remblai de pied soigneusement compacté de petite hauteur (ordre de grandeur : moins de 1/3 de la hauteur du barrage), et de longueur amont-aval suffisamment importante pour être assimilable à un remblai de longueur infinie.
La composante verticale de l'action est prise égale au poids éventuellement déjaugé des terres. La composante horizontale est calculée à partir du coefficient de pression latérale des terres au repos K0. La résultante est éventuellement corrigée pour ne pas dépasser le frottement mobilisable à l'interface barrage - remblai.
Cas d’une recharge agissant sur une grande partie de la hauteur du barrage : la recharge aval est ici un remblai appuyé sur toute ou sur une grande partie de la hauteur du barrage et contribuant de façon significative à sa stabilité.
Dans ce cas, la prise en compte de la poussée de la recharge doit toujours faire l’objet d’une étude spécifique. Cette dernière consiste en une modélisation des interactions à l’interface remblai/parement aval, incluant l’étude de la cinématique des consolidations du remblai et, le cas échéant, celle de la compressibilité des fondations qui portent le remblai. L’étude tient compte de la géométrie réelle du remblai non infini.
En première approche et pour donner simplement un ordre de grandeur, on peut procéder comme dans le premier cas en retenant le coefficient de pression latérale des terres au repos K0, mais en le minorant pour rendre compte du fait que la recharge est de dimension limitée.

Cette première approche n’est pas valable pour le cas des parements aval très raides, ou pour les remblais aval cohésifs, deux cas pour lesquels il peut y avoir réduction de la poussée par rapport à cette approche.
Dans les deux configurations (remblai de pied ou recharge de grande hauteur), des incertitudes importantes apparaissent dans la détermination de l’intensité de la poussée d’une recharge aval. Ces incertitudes portent sur les hypothèses de calcul, en particulier le choix du coefficient de poussée et l’inclinaison de la poussée, et sur la connaissance des propriétés des matériaux (angle de frottement interne, cohésion, poids volumique).
En toute hypothèse, la valeur caractéristique à retenir pour l’intensité de la poussée d’une recharge aval doit correspondre à une estimation prudente de l’intensité raisonnablement envisageable du côté des valeurs défavorables. On a deux valeurs caractéristiques pour l’action d’une recharge aval G2 : G2k-inf pour les justifications de la stabilité à retenue pleine et G2k-sup pour les justifications de la stabilité à retenue vide.
Actions des tirants précontraints G3
Deux configurations sont à distinguer :
Installation de tirants sur des barrages existants (ou lors de la construction de barrages neufs): les tirants sont ici mis en place sur le barrage lui-même ou l’un de ses ouvrages annexes (évacuateur de crues, …).
La valeur caractéristique de la force d’ancrage apportée par les tirants précontraints (quelle que soit l’inclinaison des tirants) est déduite de la traction de blocage par application d’une perte, dont on peut, en première approximation, évaluer la valeur moyenne de 6 à 10%. Cette perte est à préciser en fonction des propriétés de la fondation, des matériels et matériaux utilisés, et doit toujours faire l'objet d'une étude spécifique, selon les recommandations mentionnées dans [TA, 1995].
Notons que, dans tous les cas, les tirants doivent être réalisés selon ces mêmes recommandations, notamment en ce qui concerne les essais, la protection contre la corrosion, les modalités de contrôle de la traction et la possibilité de retendre les tirants ou d'en ajouter.
Il convient d’insister sur la nécessité de contrôler périodiquement la tension des tirants. On recommande des dispositifs fixes installés à la mise en place des tirants et équipant une proportion significative d’entre eux.
Cas des barrages avec tirants en service : il s’agit ici de justifier un barrage en service comportant des tirants plus ou moins anciens. La difficulté vient souvent du fait que l’on ne peut pas mesurer la tension résiduelle dans les tirants (c’est le cas des tirants injectés sur toute leur longueur). Il convient dans ce cas de faire preuve d’une plus grande prudence dans le cas où des indices de corrosion sont avérés, une valeur nulle pourra être retenue.
Si la mesure de la traction résiduelle est possible, on adopte pour la valeur caractéristique de la force d’ancrage une intensité raisonnablement prudente évaluée à partir des mesures réalisées in situ et tenant compte d’éventuelles pertes différées encore envisageables envisageables (à l’instar des tirants neufs, une perte comprise entre 6 et 10 % peut être retenue en première approximation). Là encore, une étude spécifique est indispensable, selon les recommandations mentionnées dans [TA, 1995].
Dans les deux configurations (installation de nouveaux tirants ou tirants en service sur des barrages anciens) et compte tenu de l’incertitude liée aux pertes instantanées et différées et des modalités de contrôle de la tension des tirants (nombre de tirants et précision des appareils de mesure), la valeur caractéristique à retenir pour l’intensité de la force d’ancrage doit correspondre à une estimation prudente de l’intensité raisonnablement envisageable du côté des valeurs défavorables (valeurs basses). Il doit également être tenu compte pour cette estimation du contexte dans lequel sont mis en place les tirants (application stricte de l'ensemble des recommandations [TA, 1995] notamment, tant au moment de la mise en place que lors de l'exploitation future de l'ouvrage).
Modélisation des actions variables de l’eau
Les actions variables comprennent les actions dont l’intensité et/ou les points d’application varient fréquemment et de façon significative dans le temps. Les actions variables sont notées Q. On considère que les actions de l’eau agissant sur les barrages, c’est-à-dire la poussée hydrostatique amont (Q1), l’action des sous-pressions (Q2), la poussée hydrostatique aval (Q3) et l’action des glaces (Q4) sont des actions variables, et ce quelles que soient l’amplitude et la fréquence du marnage de la retenue. Pour le calcul des actions de l’eau (Q1, Q2, Q3 et Q4), on détermine leurs valeurs représentatives directement dans les différentes situations de projet, en examinant dans chacune des situations les niveaux de remplissage de la retenue et les niveaux aval, et les intensités des actions qui en résultent.
Poussée hydrostatique amont Q1
Le principe du calcul de l’action de l’eau de la retenue revient à un calcul de poussée hydrostatique. Dans chaque situation de projet correspondant à un niveau de remplissage de la retenue, on calcule l’intensité Q1 résultant de la hauteur d’eau supposée connue agissant contre le parement amont : les incertitudes sur l’intensité de Q1 sont, sous cette hypothèse, limitées.
Le poids volumique de l’eau claire est pris égal à $ \gamma_w $ = 9,81 kN/m3. Toutefois, dans des cas d’écoulements fortement chargés, des valeurs supérieures peuvent être adoptées dans certaines situations particulières.
Poussée hydrostatique aval Q3
Le principe du calcul de l’action de l’eau en aval revient à un calcul de poussée hydrostatique, éventuellement corrigé d’effets hydrodynamiques.
La poussée hydrostatique aval (Q3) est obtenue dans chaque situation de projet. Elle est déduite d’un calcul de ligne d’eau dans la rivière en aval du barrage et on tient compte des cas particuliers tels que :
- des barrages avec évacuateur vanné fixant la ligne d’eau aval en fonction de l’ouverture des vannes ;
- des aménagements hydroélectriques relâchant un débit très variable ;
- de la présence d’un contre-barrage ou un barrage existant à l’aval ;
- de la présence d’un ressaut chassé en aval. Dans ce dernier cas, la contre-poussée aval n’est pas prise à compte, sauf démonstration contraire. Et il convient de considérer la largeur effective du ressaut au regard de la largeur de la rivière à l’aval.
Dans chaque situation de projet correspondant à un niveau d’eau amont, on calcule l’intensité Q3 résultant de la hauteur d’eau agissant sur le parement aval.

Action hydrodynamique
Dans le cas des barrages déversants, les actions hydrodynamiques de l’écoulement peuvent avoir un effet non négligeable et pas nécessairement stabilisateur.
Une analyse de ces actions et des éléments de calcul sont développés dans le chapitre 1.2.2.3 du document "recommandations pour la justification de la stabilité des barrages poids" (CFBR 2012) qui est téléchargeable grâce au lien suivant : http://www.barrages-cfbr.eu/Recommandations.html
Action des sous-pressions Q2
Le principe de calcul repose sur la détermination du diagramme des sous-pressions agissant dans le corps du barrage, dans l’interface barrage - fondation et dans les fondations. Ce diagramme fixe l’intensité de l’action des sous-pressions s’appliquant, soit sur les sections horizontales dans le corps du barrage, soit dans l’interface barrage - fondation, soit le long de joints rocheux dans les fondations.
Les incertitudes sur l’intensité de l’action des sous-pressions sont importantes et sont liées essentiellement aux propriétés intrinsèques du site, des matériaux et des dispositifs visant à réduire les sous-pressions (stratification de la roche de fondation, perméabilité des matériaux, qualité du voile d’injection, conception du système de drainage, etc.). Pour tenir compte de ces incertitudes, on adopte des hypothèses de répartition des sous-pressions plus ou moins sécuritaires, qui ont une influence considérable sur le dimensionnement global de l’ouvrage et sur sa sécurité. Il convient donc de retenir, pour le calcul de l’intensité des sous-pressions, des hypothèses prudentes, raisonnablement envisageables. Il est nécessaire de s’assurer, par l’auscultation, du respect au cours de la vie de l’ouvrage de la validité des hypothèses de projet adoptées pour les sous-pressions. Au cas où ces hypothèses ne seraient plus vérifiées en cours d’exploitation, des mesures s’imposeraient logiquement (vérification des conditions de sécurité, nettoyage des drains, renforcement du dispositif, etc.).
De façon générale, on considère que les variations des sous-pressions dans les fondations et dans le corps du barrage suivent le niveau de remplissage de la retenue et le niveau aval, avec un effet retard négligeable. Cette recommandation prévaut de façon générale dans toutes les situations de remplissage de la retenue, et même en situation de crue rapide et brève. Dans ces conditions, l’intensité de l’action des sous-pressions Q2 est systématiquement liée à Q1 et Q3.
On admet une seule exception à cette règle : en situation sismique, on pourra admettre que le diagramme des sous-pressions n’est pas affecté par les accélérations liées aux séismes compte tenu de leur caractère transitoire rapide, tandis que les poussées hydrostatiques sont majorées des pressions hydrodynamiques.
a) Barrages neufs ou confortement de barrages existants
Le diagramme des sous-pressions est obtenu en considérant les matériaux constituant les fondations et le corps du barrage, ainsi que les dispositifs particuliers mis en œuvre (voile d’injection, voile de drainage, masque amont). En l’absence de dispositif de drainage dans les fondations et dans le corps du barrage, on adopte, en première approche, une répartition linéaire des sous-pressions, donnant un diagramme trapézoïdal avec la pleine sous-pression en amont et une sous-pression égale au niveau d’eau en aval.
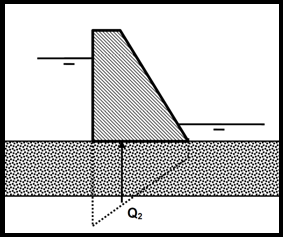
Toutefois certaines configurations peuvent donner des hypothèses plus défavorables sur la répartition des sous-pressions :
- en l’absence de drainage dans la fondation, si les fissures du rocher ont tendance à se refermer en pied aval ;
- lorsque le corps du barrage présente des fissures depuis le parement amont vers l’aval
- cas particuliers : parement aval colmaté, rejointoiement trop parfaitement étanche de ce parement…
Les dispositifs particuliers, tels que les voiles d’injection dans les fondations et les voiles de drainage en fondation et dans le corps du barrage, visant à réduire le diagramme des sous-pressions, sont pris en considération à l’aide d’un coefficient de rabattement λ et conduisent à un diagramme bilinéaire.
En adoptant les notations définies sur la figure ci-dessous, on définit le coefficient de rabattement λ par le taux suivant : λ = (Z’ – Z) / Z’

Quand le niveau de la galerie de drainage est sensiblement différent du niveau aval, il convient de tenir compte de la cote de la galerie pour la détermination du diagramme des sous-pressions. Z' et Z sont alors comptés à partir de la cote d'exutoire du drainage (Zdrain) et non pas à partir de la cote d'eau aval (Zaval).

Rabattement dans le cas où la cote de la galerie de drainage est située plus haut que le niveau aval.
La valeur du coefficient de rabattement λ dépend directement de l’efficacité du dispositif visant à réduire les sous-pressions.De nombreux facteurs peuvent avoir une influence, notamment :
- la conception et la réalisation du dispositif,
- son entretien et sa surveillance.
Le coefficient de rabattement est sujet aux variations au cours du temps, compte tenu des phénomènes de vieillissement pouvant affecter le dispositif. Il conviendra donc de s’assurer, par l’auscultation, du maintien au cours de la vie de l’ouvrage de l’efficacité du dispositif de réduction des sous-pressions.
En synthèse et dans le cas général, on recommande d’adopter les coefficients de rabattement résumés dans le tableau suivant (sauf cas particuliers de fondation) :
| Dispositif | Coefficient de rabattement λ
recommandé |
|---|---|
| dans la fondation | |
| Fondation sans voile de drainage (avec ou sans voile d’injection) | λ= 0 |
| Voile de drainage en fondation | λ= ½ à 2/3 |
| Voile de drainage en fondation, avec pendage ou géologie défavorable | λ= ½ ou moins |
| dans le corps du barrage | |
| Corps du barrage sans drainage | λ= 0 |
| Dispositif de drainage dans le corps d’un barrage en matériaux homogènes | λ= ½ à 2/3 |
| Membrane amont avec dispositif de drainage en sous face
Masque Maurice LEVY |
λ= 1 |
| Masque amont en BCV avec drainage | λ= 2/3 |
| Masque amont en BCV sans drainage | λ= 0 |
b) Vérification des barrages existants
Le diagramme des sous-pressions est obtenu comme précédemment, en tenant compte des données d’auscultation disponibles, après s’être assuré de leur représentativité et après analyse approfondie des mesures (par exemple analyse statistique HST, permettant de mettre en évidence les facteurs explicatifs des mesures et en particulier le lien entre diagramme des sous-pressions et cote de la retenue).
c) Barrage déversant ou vanné avec formation d’un ressaut hydraulique à l’aval
Sauf dispositifs particuliers d’exutoires de drainage (à justifier, y compris pour leur durabilité), le diagramme des sous-pressions est obtenu en prenant comme hauteur d’eau aval, la hauteur conjuguée à l’aval du ressaut.
d) Barrage-poids drainé et fissuré
Dans le cas d’un barrage-poids équipé de dispositifs particuliers visant à réduire les sous-pressions et lorsque le corps du barrage présente des fissures, on recommande d’adopter les hypothèses suivantes : - si la fissure ne dépasse pas le voile de drainage, on considère la pleine sous-pression dans la partie amont fissurée, puis un rabattement correspondant au coefficient de rabattement λ au droit du dispositif de drainage et enfin une répartition linéaire jusqu’au niveau hydrostatique aval ; - si la fissure dépasse le voile de drainage, on considère la pleine sous-pression dans la partie fissurée, puis une répartition linéaire jusqu’au niveau hydrostatique aval. Cette hypothèse conservative peut être nuancée si on montre que le drainage est suffisamment efficace pour rabattre les sous-pressions malgré la fissuration.
Action de la glace Q4
L’action de la glace sur les barrages n’est pas liée au phénomène physique de changement d’état (augmentation de volume à la transition liquide – solide). L’action est essentiellement d’origine thermique et correspond au phénomène de dilatation thermique de la glace, qui se produit principalement lors d’épisodes de redoux durant un hiver rigoureux. L’action de la glace concerne non seulement les barrages situés en haute altitude, mais peut également potentiellement impacter des barrages situés en zone de moyenne montagne ou en zone de plaine dont certaines ont connu des périodes de glaciation hivernale significatives ces dernières décennies. Cette action sera davantage sensible pour les barrages de petite et moyenne hauteur. Des approches quantitatives simplifiées de détermination de l’épaisseur de glace sont fournies par les recommandations [Rosa, 2000]. Elles nécessitent un échantillon de données de températures journalières sur une période suffisamment longue et représentative. En l’absence d’études plus approfondies, on peut se guider sur les dispositions suivantes :
• l’action de la glace est représentée par une pression horizontale équivalente d’intensité 150 kN/m² en zone continentale métropolitaine (eaux intérieures par opposition aux zones côtières). Cette pression est exercée sur toute l’épaisseur supposée de la glace ;
• sauf démonstration contraire, l’épaisseur de la glace minimale recommandée est de 0,30 m. Pour les retenues d’altitude, cette épaisseur est susceptible d’augmenter significativement (valeurs maximum de 60 à 80 cm). Enfin, il faut être conscient que la capacité de déformation de l’ouvrage diminue la poussée de la glace. Un calcul aux éléments finis pourra, dans ce cas, être moins défavorable qu'une modélisation simplifiée « rigide ».
Action accidentelle sismique
La démarche générale de justification des ouvrages hydrauliques vis-à-vis du risque sismique est décrite en détail dans le document :
- MEDDTL, 2010. Risque sismique et sécurité des ouvrages hydrauliques, novembre 2010, 279p.
Ce document fournit les éléments pour déterminer les sollicitations sismiques (chapitre 7.2), il décrit les méthodes de calcul pour l’analyse du comportement des ouvrages au séisme (chapitres 6.1 et 7.3 pour les ouvrages rigides), et précise les critères de sécurité à adopter (chapitre 7.3.8 pour les ouvrages rigides).
Rappel du lien accessible sur cette page :ici
Références
Carrere A. (1994). Barrages. Techniques de l’ingénieur, traité de construction.
CFBR (Comité français des barrages et réservoirs), 2012. Groupe de travail « Calcul des barrages poids » - Recommandations pour la justification de la stabilité des barrages poids – Propositions et recommandations. 117p. : http://www.barrages-cfbr.eu/Recommandations.html
CIGB (Commission Internationale des Grands Barrages), 1994. - Bulletin 93 - Vieillissement des barrages et des ouvrages annexes.
Degoutte G., Mercklé S., 2014 – Cours ISBA (Institut Supérieur du Béton Armé) – Chapitre 5 – Barrages poids.
Godart & Divet (2000). Ouvrages d’art n°34 mai 2000 20p « une nouvelle réaction de gonflement interne des bétons : la réaction sulfatique ».
Ministère de l’écologie, du développement durable et de l’énergie (MEDDE), 2014. Risque sismique et sécurité des ouvrages hydrauliques. 279 p.
Ministère de l’agriculture, Direction de l’aménagement (1977). Techniques des barrages en aménagement rural. 325p., réédition 1989.
Ministère de l’Industrie (2003)- service technique de l’Energie Electrique et de Grands Barrages. « Classification des barrages vis-à-vis des séismes » version décembre 2003.
Peyras, L. - 2003. Diagnostic et analyse de risques liés au vieillissement des barrages, développement de méthodes d'aide à l'expertise. Doctorat spécialité Génie civil, école doctorale des sciences pour l'ingénieur, laboratoire d'études et de recherches en mécanique des structures (LERMES), Université Blaise Pascal, Clermont II. 254 p.
Peyras L., Boissier D. & Carvajal C. (2010). Analyse de risques et fiabilité des barrages, application aux barrages poids en béton.
Pour plus d'information sur l'auteur : INRAE - UMR RECOVER - Equipe G2DR
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS