Izzard (modèle de) (HU) : Différence entre versions

Version du 19 septembre 2019 à 11:33

Traduction anglaise : Izzard's model

Modèle empirique (créé en 1946) de représentation de la transformation pluie nette - débit à l'exutoire d'un bassin versant [Izzard, 1946].

Sommaire

1 Hypothèses et formulation
2 Choix des paramètres
3 Utilisation pratique
4 Intérêt et limites

Hypothèses et formulation

Le modèle d'Izzard est fondé sur les éléments suivants :

· L'indépendance entre la fonction de transfert et la pluie à l'origine du ruissellement (linéarité du phénomène). Cette hypothèse permet de déduire l'existence d'un hydrogramme sans dimension représentant la réponse du bassin versant à une pluie unitaire constante. Cet hydrogramme sans dimension utilise des variables normées pour les débits et les temps. Les normes sont respectivement le débit à l'équilibre : Qeq et le temps d'équilibre : teq. Le temps d'équilibre est défini arbitrairement comme le temps au bout duquel le débit observé devient égal à 97% du débit d'équilibre :

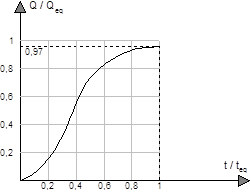
Hydrogramme sans dimension de Izzard d'après [Deutsch & al., 1989].

· L'existence de relations empiriques entre les deux grandeurs de base (Qeq et teq), le stockage superficiel instantané (De), l'intensité moyenne de pluie nette (in) et les données caractérisant le bassin versant :

Avec :

· c : paramètre fonction de la nature du revêtement ;

· De : volume stocké par unité de largeur (m3 /m) ;

· I : pente de la surface (m /m) ;

· in : intensité de pluie nette constante (mm /h) ;

· L : longueur du ruissellement (m) ;

· Qeq : débit (m3 /s /m) ;

· teq : temps (minutes).

Choix des paramètres

Le tableau suivant donne quelques indications pour le choix de c

Nature du revêtement	c
Asphalte très lisse	0,0070
Sable et goudron	0,0075
Toile goudronnée / (toiture)	0,0082
Béton en bon état	0,0120
Goudron et gravier / (voirie)	0,0170
Gazon dense tondu / (terrain de sport)	0,0460
Herbe dense (pelouse)	0,0600

Valeurs à attribuer au coefficient de rugosité c de la formule de Izzard en fonction de la nature de la surface d'écoulement, d'après [Deutsch & al., 1989].

Utilisation pratique

Le modèle d’Izzard peut fournir un hydrogramme complet à l'exutoire correspondant à un hyétogramme quelconque. Il suffit de décomposer le hyétogramme en pas de temps d'intensité constante et d'appliquer la méthode à chacune des averses élémentaires d'intensité constante ainsi obtenues. La réponse à l'entrée complète sera obtenue en sommant les réponses à chacune des entrées élémentaires (principe de superposition des solutions). Cette technique nécessite cependant d'associer à l'hydrogramme sans dimension qui ne représente que la montée en débit, une fonction permettant de représenter la décrue correspondant à chaque pluie élémentaire. Cette fonction se calcule de la façon suivante : à la fin de chaque période de pluie élémentaire, il reste sur le sol un stock D0, due à cette pluie élémentaire, égal au volume précipité moins le volume écoulé. Durant la période de décrue de l'hydrogramme élémentaire, il existe une relation empirique entre le débit à l'instant tr (temps écoulé depuis la fin de la pluie élémentaire d'intensité constante) et le débit Qd à la fin de cet instant :

Avec :

Intérêt et limites

Elaboré à l'origine pour représenter le ruissellement sur des aéroports, ce modèle s'applique bien à l'étude du ruissellement sur des routes ou des autoroutes. Il a d'ailleurs été à l'origine de la « méthode des temps d'équilibre » utilisée en France pour l'assainissement des autoroutes. D'une façon plus générale, il convient bien à des écoulements sur des éléments plans homogènes, de pente relativement faible (moins de 4%). En revanche, son application à des bassins versants urbains de surface supérieure à quelques hectares, fortement équipés en ouvrages souterrains d'assainissement, est à proscrire.

Pour en savoir plus : [Deutsch et al., 1989] : Groupe de Travail du STU animé par Deutsch J.C. ; « Mémento sur l'évacuation des eaux pluviales » ; La documentation française ; Paris ; 349 p. ; 1989.