Colebrook (formule de) (HU) : Différence entre versions

Version du 21 janvier 2020 à 10:25

Traduction anglaise : Colebrook's formula

Rubrique de rattachement : Mécanique des fluides et hydraulique (HU)

Dernière mise à jour : 21/1/2020

Formule, appelée parfois formule de Colebrook-White, initialement développée pour calculer les pertes de charge dans le cas des écoulements en charge. Cette formule permet également d'évaluer le paramètre $ C $ de l'équation de Chézy.

Sous sa forme originale, l'équation de Colebrook s'écrit :

$ \frac{1}{\sqrt{λ}} = -2.log\left(\frac{k}{a.R_h}+\frac{b}{R_e.\sqrt{λ}}\right) \quad (1) $

Dans cette relation, $ R_e $ est le nombre de Reynolds :

$ R_e = \dfrac{4.V.R_h}{ν} \quad (2) $

avec :

$ λ $ : coefficient de Colebrook (sans dimension) ;
$ g $ : accélération de la pesanteur ($ m/s^2 $) ;
$ k $ : rugosité des parois ($ m $) ;
$ R_h $ : rayon hydraulique ($ m $) ;
$ ν $ : viscosité cinématique du fluide ($ m^2/s $) ;
$ a $ et $ b $ : coefficients sans dimension (12 < $ a $ < 15 et 0 < $ b $ < 6).

Les pertes de charge se calculent par la relation :

$ J = λ.\dfrac{V^2}{8.g.R_h} \quad (3) $

Pour un écoulement à surface libre, en régime uniforme, la pente de la ligne d'énergie est parallèle à la pente du fond, donc $ I = J $. On peut donc écrire :

$ I = λ.\dfrac{V^2}{8.g.R_h} \quad\quad \Longrightarrow \quad\quad \dfrac{1}{\sqrt{\lambda}} = \dfrac{V}{\sqrt{8.g.R_h.I}} \quad(4) $

En reportant les expressions (2) et (4) dans la relation (1), on obtient une formulation explicite de $ λ $ :

$ \dfrac{1}{\sqrt{λ}} = -2.log[\frac{k}{a.R_h}+\frac{b.ν}{8.R_h\sqrt{2.g}.\sqrt{R_h.I}}] \quad (5) $

La relation (4) permet également d'écrire :

$ V = \dfrac{1}{\sqrt{λ}}.\sqrt{8.gR_h.I} = C.\sqrt{R_h.I} \quad(6) $

avec

$ C = \dfrac{1}{\sqrt{λ}}\sqrt{8.g} \quad(7) $

En reportant la relation (5) dans l'expression (7), on obtient finalement une expression explicite du coefficient C de Chezy :

$ C = -4\sqrt{2.g}.log \left(\frac{k}{a.R_h}+\frac{b.ν}{8.R_h\sqrt{2.g.R_h.I}}\right) \quad(8) $

Les valeurs généralement retenues pour a et b sont les suivantes :

$ a $ = 14,8
$ b $ = 2,51

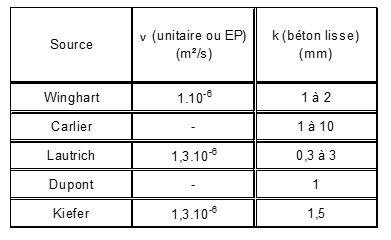
Le tableau suivant donne des indications sur le choix de k et :

Valeurs indicatives pour le choix de $ ν $ et $ k $.

Il est important de préciser que la rugosité des parois doit tenir compte, non seulement de la dimension des aspérités, mais également des macro-obstacles à l'écoulement que l'on peut rencontrer dans les systèmes d’assainissement : coudes, chutes, câbles accrochés aux parois, etc.

Bibliographie :

Carlier, M. (1972) : Hydraulique générale et appliquée ; Eyrolles ; Paris ; 565 p. ; 1972.
Lautrich, R. (1971) : Tables et abaques pour le calcul hydraulique des canalisations sous pression, égouts et caniveaux ; Eyrolles ; 1971.
Winghart, M. : Cours polycopié de mécanique des fluides et d'hydraulique ; INSA de Lyon - département GCU ; non daté.

Voir aussi : Coefficient de rugosité, Perte de charge.

@@ Ligne 86 : / Ligne 86 : @@
 * Carlier, M. (1972) : Hydraulique générale et appliquée ; Eyrolles ; Paris ; 565 p. ; 1972.
 * Lautrich, R. (1971) : Tables et abaques pour le calcul hydraulique des canalisations sous pression, égouts et caniveaux ; Eyrolles ; 1971.
-* Winghar,t M. : Cours polycopié de mécanique des fluides et d'hydraulique ; INSA de Lyon - département GCU ; non daté.
+* Winghart, M. : Cours polycopié de mécanique des fluides et d'hydraulique ; INSA de Lyon - département GCU ; non daté.
 <u>Voir aussi</u> : [[Coefficient de rugosité (HU)|Coefficient de rugosité]], [[Perte de charge linéaire (HU)|Perte de charge]].
 [[Catégorie:Dictionnaire_DEHUA]]

Colebrook (formule de) (HU) : Différence entre versions

Version du 21 janvier 2020 à 10:25

Affichages

Outils personnels