Spline (fonction) (HU) : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Spline function'' | ''<u>Traduction anglaise</u> : Spline function'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 16/09/2021 |
| − | Méthode d'interpolation analytique parfois utilisée pour représenter des champs de précipitations observés | + | Méthode d'interpolation analytique parfois utilisée pour représenter des champs de précipitations observés. |
| − | [[File: | + | ==Principes de la méthode== |
| + | |||
| + | Cette méthode est à l'origine issue de considérations mécaniques reposant sur le constat qu'une poutre mince (à une dimension) ou une plaque mince (à deux dimensions) soumise à des efforts de flexion, se déforme en minimisant son énergie interne. | ||
| + | |||
| + | La généralisation en terme d'interpolation consiste à faire passer un polynôme d'interpolation de degré adéquat par tous les points de mesure tout en minimisant l'équivalent numérique de l'énergie de flexion. Cette dernière condition assure la continuité des pentes et des courbures et permet l'obtention de fonctions à une ou plusieurs dimensions d'aspect lisse. | ||
| + | |||
| + | |||
| + | [[File:spline.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Exemple d'interpolation par une fonction spline ; <>Source<>.: https://support.ptc.com/help/creo/ced_modeling/r20.2.0.0/fr/index.html#page/ced_modeling/OSDM_Main/3DCurves_Spline.html''</center>]] | ||
| + | |||
| + | <u>Nota</u> : L'interpolation peut éventuellement se faire par morceaux en imposant des conditions complémentaires de continuité des valeurs et des pentes. | ||
| + | |||
| + | <u>Pour en savoir plus sur les fonctions spline</u> : Voir l'[https://fr.wikipedia.org/wiki/Spline article de Wipidédia]. | ||
| + | |||
| + | ==Utilisation pour représenter la répartition spatiale des précipitations== | ||
| + | |||
| + | Les pluies sont souvent connues par des mesures ponctuelles effectuées au sol sur un réseau de pluviomètres. Il est donc nécessaire d'interpoler les mesures pour connaître les intensités ou les hauteurs d'eau en tous points (voir | ||
| + | Pour un champ pluvieux donné, décrit par N valeurs ponctuelles mesurées, les deux conditions précédentes mènent à un système de N+3 équations à N+3 inconnues. Cette méthode ne repose sur aucune hypothèse réaliste concernant la structure des champs de pluie. | ||
| + | |||
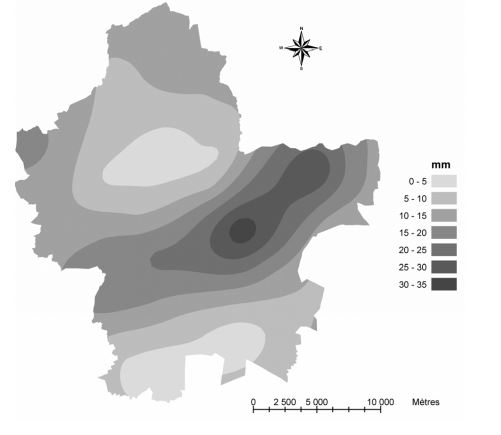
| + | [[File:krigeage.JPG|600px|center|thumb|<center>''<u>Figure 2</u> : Représentation d'un champ de pluie par une fonction spline ; d'après Renard & Comby (2007).''</center>]] | ||
<u>Bibliographie</u> : | <u>Bibliographie</u> : | ||
Version du 16 septembre 2021 à 13:47
Traduction anglaise : Spline function
Dernière mise à jour : 16/09/2021
Méthode d'interpolation analytique parfois utilisée pour représenter des champs de précipitations observés.
Principes de la méthode
Cette méthode est à l'origine issue de considérations mécaniques reposant sur le constat qu'une poutre mince (à une dimension) ou une plaque mince (à deux dimensions) soumise à des efforts de flexion, se déforme en minimisant son énergie interne.
La généralisation en terme d'interpolation consiste à faire passer un polynôme d'interpolation de degré adéquat par tous les points de mesure tout en minimisant l'équivalent numérique de l'énergie de flexion. Cette dernière condition assure la continuité des pentes et des courbures et permet l'obtention de fonctions à une ou plusieurs dimensions d'aspect lisse.

Nota : L'interpolation peut éventuellement se faire par morceaux en imposant des conditions complémentaires de continuité des valeurs et des pentes.
Pour en savoir plus sur les fonctions spline : Voir l'article de Wipidédia.
Utilisation pour représenter la répartition spatiale des précipitations
Les pluies sont souvent connues par des mesures ponctuelles effectuées au sol sur un réseau de pluviomètres. Il est donc nécessaire d'interpoler les mesures pour connaître les intensités ou les hauteurs d'eau en tous points (voir Pour un champ pluvieux donné, décrit par N valeurs ponctuelles mesurées, les deux conditions précédentes mènent à un système de N+3 équations à N+3 inconnues. Cette méthode ne repose sur aucune hypothèse réaliste concernant la structure des champs de pluie.
Bibliographie :
- Renard, F & Comby, J. (2007): Caractérisation de l’aléa pluviométrique en milieu urbain à partir d’interpolations spatiales : le cas du Grand Lyon ; Climatologie, 2007, p. 131-144. téléchargeable sur : http://lodel.irevues.inist.fr/climatologie/index.php?id=782
Voir aussi : Géostatistique, Krigeage (HU).
 S'abonner à un flux RSS
S'abonner à un flux RSS