S'abonner à un flux RSS
 

Temps de concentration (HU) : Différence entre versions

De Wikhydro
(→‎Cas des bassins versants urbains)
Ligne 103 : Ligne 103 :
  
  
−
<center><math>K = 0{,}494.A^{-0,0076}.C_{IMP}^{-0,512}.I^{-0,401}.L^{0,608}\quad(9)</math></center>
+
<center><math>formule provisoirement supprimée - erreur coefficients\quad(9)</math></center>
  
  

Version du 6 janvier 2022 à 20:41

Traduction anglaise : Time of concentration

Dernière mise à jour : 09/12/2021

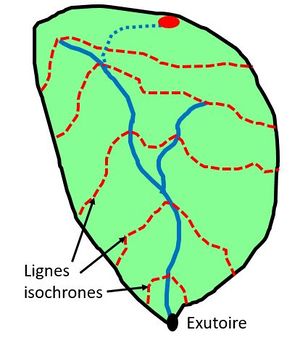
Sur un bassin versant, temps mis par l'eau pour parcourir la distance entre le point le plus éloigné (en temps d’écoulement) de l'exutoire et ce dernier.


Figure 1 : Représentation schématique d'un bassin versant. Le point noir en bas de l'image est l'exutoire ; les lignes en pointillés rouge représentent des lignes isochrones et le point rouge est le point le plus éloigné de l'exutoire. Le temps de concentration est le temps nécessaire pour aller de ce point jusqu'à l'exutoire.

Sommaire

Origine et importance de la notion de temps de concentration

Temps de concentration et calcul du débit de pointe du bassin versant

La notion de temps de concentration aurait été introduite, pour la première fois en 1851, par un physicien irlandais, T.J. Mulvaney comme le temps au bout duquel apparait le débit de pointe à l’exutoire d’un bassin versant. Le temps de concentration constitue le paramètre de base dans la méthode rationnelle ainsi que dans certains autres modèles pluie-débit de même nature (méthode de Caquot par exemple) pour le calcul des débits de pointe des bassins versants.

Si l'on considère une pluie de type bloc (intensité constante) et répartie uniformément sur le bassin versant, la pluie la plus défavorable, c'est à dire qui conduira au débit de pointe maximum, pour une période de retour donnée est celle dont la durée est strictement identique au temps de concentration.

En effet :

  • si la durée de la pluie est plus courte que le temps de concentration alors seule une partie de la surface du bassin versant contribuera à chaque instant au débit à l'exutoire, donc, en particulier, au moment où ce débit est le pus grand  ;
  • si la durée de la pluie est plus longue que le temps de concentration alors l'intensité de pluie sera plus faible pour une même période de retour.

Conséquences hydrologiques de la réduction du temps de concentration

Au delà de la vision précédente, sans doute assez simpliste vis à vis de la complexité des phénomènes hydrologiques en cause, la prise en compte de cette notion est essentielle pour comprendre les conséquences des aménagements sur la réponse des bassins versants. En effet réduire le temps de concentration d'un bassin versant a deux effets très préjudiciables sur la valeur des débits :

  • elle rend le bassin versant sensibles à des pluies plus courtes, donc dont l'intensité moyenne est plus forte et qui vont générer des volumes plus importants par unité de surface ;
  • elle diminue également le temps de réponse du bassin versant (voir Lag time (HU)), ce qui a pour conséquence que le volume produit, déjà plus important, s'écoule dans un temps plus court ce qui augmente mécaniquement la valeur du débit maximum et diminue le temps d'alerte.

Ces deux facteurs font que la diminution des temps de concentration résultant de l'aménagement des bassins versants constitue souvent le facteur essentiel de l'aggravation du régime des crues alors que l'on accuse souvent à tort l'augmentation des coefficients de ruissellement.

Évaluation du temps de concentration d'un bassin versant

Le temps de concentration peut être soit apprécié par la mesure à partir de crues observées, soit estimé.

Fondements théoriques de l'évaluation du temps de concentration

On peut trouver des fondements théoriques de l'évaluation du temps de concentration, selon la conception de Mulvaney, en utilisant le modèle de l’onde cinématique pour représenter le ruissellement de la pluie sur une plaque plane homogène de rugosité $ k $ et de longueur de ruissellement $ L $, soumise à une précipitation d’intensité constante $ i $.

Dans ces conditions, le temps au bout duquel apparaît le débit de pointe de ruissellement à l’exutoire de la plaque s’écrit :


$ t_c = (\frac{L.i^{(1-m)}}{k})^{1/m} \quad(1) $

Dans cette expression, $ m $ est l’exposant de la formule d’écoulement du régime uniforme (par exemple 3/2 dans la formule de Chezy). Cette relation montre, en particulier, et contrairement à de multiples formules usuelles en ingénierie, que le temps de concentration d’un bassin versant n’est pas constant et dépend de l’intensité de la pluie nette.

Formules empiriques de calcul du temps de concentration

En réalité, dès que les surfaces dépassent quelques hectares (au maximum quelques dizaines d'hectares pour des bassins versants très plats), on s'éloigne des hypothèses précédentes qui correspondent à un ruissellement en lame mince. Dans les bassins versants naturels, les écoulements s'organisent assez vite, d'abord dans des thalwegs secs, puis dans des cours d'eau de plus en plus importants et pérennes. Dans les bassins versants aménagés, et particulièrement dans les bassins versants urbains, c'est un réseau de plus en plus artificiel qui structure le transfert. Ceci explique que l'on évalue généralement le temps de concentration à partir de formules empiriques faisant intervenir des caractéristiques du bassin versant (surface, pourcentage de surface imperméable, pente, etc.), voire de la pluie. Il existe un très grand nombre de formules qui ne sont généralement valides que dans le domaine où elles ont été construites. Nous rappelons quelques unes des formules les plus classiques dans les § suivants en distinguant le cas des bassins versants ruraux ou naturels et le cas des bassins versants urbains.

Pour toutes ces formules on utilise les unités peu orthodoxes suivantes :

  • $ A $ : Surface du bassin versant (en $ hectares $) ;
  • $ L $ : Longueur du plus long parcours de l'eau ($ m $) ;
  • $ I $ : pente (%) ;
  • $ t_c $ : temps de concentration ($ mn $).


Cas des bassins versants ruraux ou naturels

Parmi les plus classiques on trouve les formules suivantes :

Formule de Passini, établie pour des bassins versants ruraux de surface supérieure à 4 000ha :


$ t_c = 1{,}44 \frac{\left(A.L\right)^{1/3}}{\sqrt{I}} \quad(2) $

Formule de Turraza :


$ t_c = 6{,}51\sqrt{A} \quad(3) $

Formule de Ventura, établie pour des bassins versants ruraux de surface supérieure à 1 000ha :


$ t_c = 7{,}62\sqrt{\frac{A}{I} }\quad(4) $

Formule de Giandotti :


$ t_c = 600\frac{0{,}04.\sqrt{A}+0{,}0015.L}{0{,}8.\sqrt{I.L}}\quad(5) $


Cas des bassins versants urbains

Dans les bassins versants urbains, le transfert se fait principalement dans un système hydrologique aménagé : caniveaux et branchements, puis réseau de conduites souterraines. Les formules précédentes ne s'appliquent pas, les écoulements étant beaucoup plus rapides que dans des biefs naturels. Les formules à utiliser sont donc différentes.

Le memento ASTEE (2018) propose d'utiliser la formule de Kirpich :


$ t_c = 0{,}115.\left[ \frac{L}{\sqrt{I}} \right]^{0,77}\quad(6) $


Cette formule est encore souvent majorante et il paraît plus logique d'utiliser une formule faisant directement intervenir la longueur du plus long parcours de l'eau ($ L $) et la vitesse moyenne d'écoulement ($ V $) :


$ t_c = \frac{1}{60}\frac{L}{V} \quad(7) $

La vitesse moyenne augmente avec la pente du bassin versant mais, pour des raisons techniques, elle est généralement comprise entre des bornes assez strictes. Elle est généralement supérieure à $ 1\ m/s $ pour vérifier des conditions d'autocurage et inférieure à $ 2\ m/s $ pour limiter l'érosion et la dégradation des ouvrages.

La meilleure solution semble cependant de repartir des relations proposées pour évaluer les lag times des bassins versants, en considérant, suite aux travaux de Thibault (2011), que la valeur du lag time est comprise entre la moitié et les deux tiers de la valeur du temps de concentration. On peut par exemple utiliser les relations proposées par Desbordes (1974) pour le paramètre $ K $ du modèle du réservoir linéaire. Ces relations ont en effet l'intérêt de faire intervenir le coefficient d'imperméabilisation qui traduit le niveau d'urbanisation du bassin versant :


$ K =3{,}71.A^{0,394}.C_{IMP}^{-0,452}.I^{-0,383}\quad(8) $


$ formule provisoirement supprimée - erreur coefficients\quad(9) $


$ K = 3{,}55.A^{0,27}.(1 + C_{IMP})^{-1,9}.I^{-0,36}.L^{0,15}.D_p^{0,21}.H_p^{-0,07}\quad(10) $

On peut ensuite calculer $ t_c $ en fonction de $ K $.

$ t_c = a.K\quad(11) $

Avec :

  • $ A $ : surface du bassin versant ($ hectares $) ;
  • $ D_p $ : durée de la période de "pluie critique" du bassin (de l'ordre de grandeur du temps de réponse du bassin) ($ mn $) ;
  • $ H_p $ : hauteur de pluie pendant cette durée ($ mm $) ;
  • $ I $ : pente du plus long parcours (%) ;
  • $ C_{IMP} $ : coefficient d'imperméabilisation (en rapport, c'est à dire compris entre $ 0 $ et $ 1 $) ;
  • $ L $ : longueur du plus long parcours de l'eau (collecteur principal) ($ m $) ;
  • $ a $ : paramètre sans dimension valant $ 2 $ pour un réseau linéaire et tendant vers $ 1{,}5 $ lorsque le réseau se développe ;

Bibliographie :

Récupérée de « http://wikhydro.developpement-durable.gouv.fr/index.php?title=Temps_de_concentration_(HU)&oldid=45692 »
Outils personnels

Milieux


Territoires


Savoirs / Acteurs


Enjeux