Mécanique des fluides numérique / MFN (HU) : Différence entre versions
(→Domaines d'utilisation en hydrologie urbaine) |
|||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Computational Fluid Dynamics / CFD'' | ''<u>Traduction anglaise</u> : Computational Fluid Dynamics / CFD'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 18/01/2023 |
''mot en chantier'' | ''mot en chantier'' | ||
| Ligne 102 : | Ligne 102 : | ||
Les [[Déversoir d'orage (HU)|déversoirs d’orage]] font sans doute partie des ouvrages présents dans les réseaux d'assainissement et pour lesquels les apports de la MFN sont les plus utiles. Ces ouvrages jouent en effet un rôle très importants dans le fonctionnement des réseaux en conditionnant les [[Rejet urbain de temps de pluie / RUTP (HU)|rejets urbains de temps de pluie]] et leur fonctionnement hydraulique, souvent compliqué, est très mal représenté par les méthodes classiques de simulation (en général [[Barré de Saint Venant (équations de) (HU)|équations de Barré de saint venant]]). | Les [[Déversoir d'orage (HU)|déversoirs d’orage]] font sans doute partie des ouvrages présents dans les réseaux d'assainissement et pour lesquels les apports de la MFN sont les plus utiles. Ces ouvrages jouent en effet un rôle très importants dans le fonctionnement des réseaux en conditionnant les [[Rejet urbain de temps de pluie / RUTP (HU)|rejets urbains de temps de pluie]] et leur fonctionnement hydraulique, souvent compliqué, est très mal représenté par les méthodes classiques de simulation (en général [[Barré de Saint Venant (équations de) (HU)|équations de Barré de saint venant]]). | ||
| − | L'exemple suivant illustre la simulation d'un déversoir frontal fonctionnant en régime fluvial à l'amont et en régime torrentiel à l'aval de façon à mieux contrôler les débits conservés. La modélisation hydrodynamique permet de vérifier le bon fonctionnement de ce type d’ouvrage pour les sollicitations les plus fortes (période de retour de 10 ans par exemple). | + | L'exemple suivant (''figure 5'') illustre la simulation d'un déversoir frontal fonctionnant en régime fluvial à l'amont et en régime torrentiel à l'aval de façon à mieux contrôler les débits conservés. La modélisation hydrodynamique permet de vérifier le bon fonctionnement de ce type d’ouvrage pour les sollicitations les plus fortes (période de retour de 10 ans par exemple). |
| − | |||
| + | [[File:MFN_DO_JV.png|600px|center|thumb|<center>''<u>Figure 5</u> : Évolution de la surface libre dans un déversoir frontal - voir les conditions de réalisation de l'étude dans le tableau de la figure 6 ; Crédit José Vasquez.''</center>]] | ||
| + | [[File:mfn_do.JPG|600px|center|thumb|<center>''<u>Figure 6</u> : Conditions de réalisation de l'étude.''</center>]] | ||
| − | + | L'utilisation de modèles de MFN pour représenter ce type d'ouvrages permet d'évaluer les incertitudes associées aux représentations classiques et éventuellement de proposer des modélisations simplifiées alternatives. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | L'utilisation de modèles de MFN pour représenter ce type d'ouvrages permet d'évaluer les incertitudes associées aux représentations classiques et éventuellement de proposer des modélisations simplifiées alternatives | + | |
| + | <u>Nota</u> : Une utilisation particulière des outils de MFN pour ce type d'ouvrage (qui doivent être instrumentés dans le cadre de l'[[Autosurveillance (HU)|autosurveillance]]) est l'optimisation du positionnement des sondes. Les capteurs les plus performants sont en effet les capteurs de niveau. Le calcul du débit déversé connaissant la hauteur d'eau s'effectue ensuite en appliquant une loi de seuil. La difficulté réside dans le fait que la ligne d'eau le long du seuil peut être très variable et très perturbée. Si le capteur n'est pas installé au bon endroit sa mesure peut ne pas être représentative de la forme réelle de la ligne d'eau et les calculs de débit sont alors entachés d'une grande incertitude. L'utilisation d'outils de CFD permet de choisir de façon efficace la meilleure position des sondes et de paramétrer correctement la loi de seuil (Mignot ''et al'', 2011). | ||
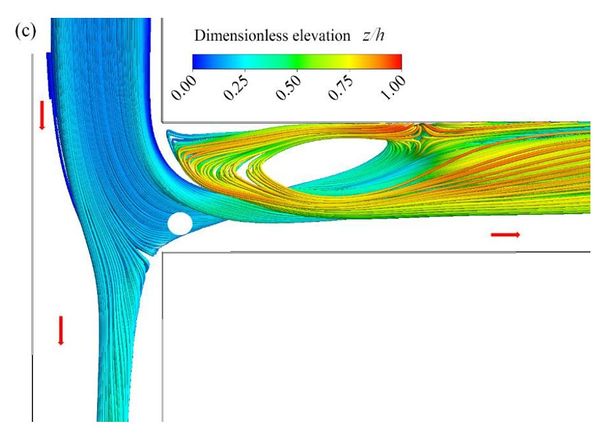
[[File:mfn6.JPG|600px|center|thumb|<center>''<u>Figure 5</u> : Les résultats obtenus dans ce cas sur la défluence représentée à la ''figure 4'' montre que, selon la position, le rapport entre la hauteur d'eau et la charge hydraulique varie entre 0 et 1, ce qui est contradictoire avec les hypothèses le plus souvent retenues dans les outils de simulation des réseaux ; noter également la présence d'une importante recirculation ; <u>Source</u> : Monplot (2014).''</center>]] | [[File:mfn6.JPG|600px|center|thumb|<center>''<u>Figure 5</u> : Les résultats obtenus dans ce cas sur la défluence représentée à la ''figure 4'' montre que, selon la position, le rapport entre la hauteur d'eau et la charge hydraulique varie entre 0 et 1, ce qui est contradictoire avec les hypothèses le plus souvent retenues dans les outils de simulation des réseaux ; noter également la présence d'une importante recirculation ; <u>Source</u> : Monplot (2014).''</center>]] | ||
Version du 18 janvier 2023 à 13:00
Traduction anglaise : Computational Fluid Dynamics / CFD
Dernière mise à jour : 18/01/2023
mot en chantier
Ensemble de méthodes numériques utilisant la capacité de calcul d’un ordinateur et permettant de quantifier les écoulements de fluides en résolvant les équations de conservation : de la masse, de la quantité de mouvement et de l’énergie ainsi que de tous autres phénomènes associés tels que le transport de solide et les réactions chimiques par exemple.
Dans le domaine de l'hydraulique, la MFN concerne en particulier la résolution des équations de Navier-Stokes pour une géométrie donnée.
Sommaire |
Principes
Le principe de base consiste à transformer un phénomène représenté par des équations différentielles ou des EDP sur un domaine physique continu par un système d'équations algébriques prenant des valeurs sur un domaine discret, puis à résoudre ces équations algébriques en utilisant un solveur plus ou moins générique mis en œuvre par un logiciel adéquat.
Le choix des équations, les discrétisations et les méthodes de résolutions vont dépendre du type d’écoulement à modéliser. La mise en œuvre de la méthode nécessite plusieurs étapes.
Étape 1 : Analyse physique de l’écoulement à étudier ; différents éléments doivent être pris en compte et il est en particulier nécessaire de répondre aux questions suivantes :
- Quel est l'environnement de l’écoulement (milieu confiné ou non) ?
- si le milieu est confiné, l’écoulement se produit dans un lieu entouré de paroi (par exemple étude d’un déversoir ou d'un bassin) ; si l'une des parois est mobile, l’interaction fluide structure sera à prendre en compte dans la méthode de résolution des équations ainsi que dans le maillage ;
- si le milieu n'est pas confiné, l’écoulement a lieu dans un environnement infini (par exemple étude d’une hélice ou une hydrolienne) ; dans ce cas les conditions aux limites du modèle doivent être définies ;
- De quel fluide s'agit-il et quelles sont ses lois de comportement ?
- le fluide est-il compressible ou incompressible (dans le cas d'un fluide compressible les variations de pression peuvent engendrer une variation de la masse volumique du fluide impactant le champ de pression ainsi que le champ de vitesse) ;
- le fluide a-t-il un comportement newtonien (cas de l’eau et de l’air) ou non newtonien comme une coulée de boue.
- L'écoulement est-il mono ou multiphasique ? dans le cas d'un écoulement multiphasique, il faudra en plus savoir s’il s’agit de fluides miscibles ou non ;
- Nota : Dans le cas des écoulements à surface libre, on utilise généralement deux fluides considérés comme non miscibles et la détermination de la surface libre nécessite une procédure particulière de recherche de l’interface entre l’eau et l’air ;
- Est-il nécessaire de prendre en compte des phénomènes thermiques ? si oui, la prise en compte d’une source de chaleur introduit des équations supplémentaires ;
- Quel type d'écoulement faut il prendre en compte ?
- Écoulement laminaire ou turbulent : si l'écoulement est turbulent (ce qui sera presque toujours le cas en hydrologie et en assainissement) il faudra choisir un modèle de turbulence adapté ;
- Écoulement stationnaire ou transitoire : il s’agit de savoir si l’évolution en transitoire des caractéristiques de l’écoulement est une donnée importante dans l’analyse des résultats ;
- Nota : Dans certains cas, même la prise en compte de conditions aux limites permanentes peut produire des instabilités hydrodynamiques qui restent transitoires ;
- Faut-il prendre en compte le transport de particules ? (cas du transport solide) ;
- Faut-il prendre en compte les changements de phase ? (cas de la cavitation) ;
- Faut-il prendre en compte le transport de bulles ? (cas de l'aération des bassins biologiques ou des chutes d’eau).
Étape 2 : Choix d'une formulation et, par association, d'une méthode de mise en équations en lien avec l’analyse physique de l’écoulement ; trois méthodes, que l'on peut coupler, sont utilisables :
- approximation des dérivées des variables par des opérateurs algébriques et méthode des différences finies ;
- approximation des variables (forme intégrale) par des opérateurs algébriques en utilisant la formulation variationnelle et méthode des éléments finis (formulation faible) ;
- approximation directe des variables (forme intégrale) par des opérateurs algébriques et méthode des volumes finis (formulation forte).
Étape 3 : Délimitation du domaine d'étude et maillage de ce domaine en lien avec la méthode précédemment choisie.
Étape 4 : Choix des conditions aux limites et construction des équations algébriques correspondantes sur les différents "bords" du domaine d'étude de façon que le nombre d'équations soit égal au nombre d'inconnues.
Étape 5 : Utilisation d’outils graphiques et numériques pour représenter les résultats.
Choix de la méthode
La plupart des logiciels utilisent la méthode des volumes finis pour discrétiser les opérateurs dans l'espace (Versteeg, et al., 1995). Cette méthode consiste en effet à écrire, sur chaque volume élémentaire, que la variation interne de la grandeur considérée (masse, énergie, quantité de mouvement) est égale à la somme des flux qui traversent sa frontière ; elle est donc conservative par construction. Si nécessaire (dans le cas des phénomènes évolutifs), la méthode des différences finies peut être utilisée en complément pour discrétiser les dérivées sur le temps.
Choix du maillage
Le maillage a pour but de subdiviser le domaine spatial de calcul en un grand nombre de petits éléments appelés cellules. Ces cellules sont des segments dans le cas 1D, des surfaces dans le cas 2D ou des volumes dans le cas 3D.
Dans le cas de la méthode des volumes finis les grandeurs sont calculées en un point particulier de chacune des cellules appelé centre. La méthode des volumes finis est très souple et les cellules peuvent prendre des formes quelconques ; de plus, leurs formes, comme leur taille, peuvent varier selon la position.
La taille des cellules constituant le maillage joue un rôle considérable sur la qualité des résultats de la modélisation. En effet, les valeurs calculées dans chaque cellule sont supposées constantes. Si leur volume est grand dans un domaine de l’écoulement où les gradients sont forts, il en résultera une mauvaise résolution des équations et des résultats erronés. Pour éviter ce risque, il est nécessaire de raffiner le maillage dans les zones de fort gradient.
Un problème particulier est posé par les écoulements en proche paroi (couche limite) où les gradients de vitesse et de pression sont très forts. Il est possible sur ces zones de raffiner beaucoup le maillage ou d'utiliser une solution alternative consistant à ajouter une équation supplémentaire représentant un modèle spécifique de couche limite.
Le maillage a pour but de subdiviser le domaine spatial de calcul en un grand nombre de petits éléments appelés cellules. Ces cellules sont des segments dans le cas 1D, des surfaces dans le cas 2D ou des volumes dans le cas 3D.
Le maillage doit de plus vérifier deux conditions :
- il doit recouvrir totalement le domaine et en particulier les bords des cellules voisines des limites doivent correspondre aux bords du domaine ;
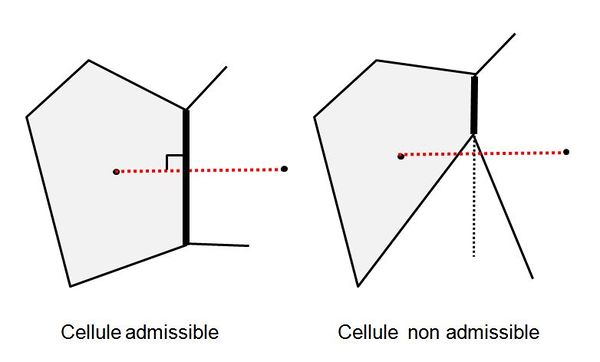
- il doit être "admissible", c'est à dire que chaque cellule doit posséder un centre tel que chaque ligne joignant ce centre aux centres de chacune des cellules voisines doit obligatoirement être normal à la frontière entre ces cellules et passer par cette frontière (figure 1).
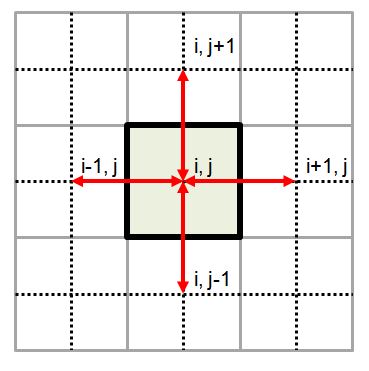
Dans le cas d'un maillage régulier, on parle de maillage structuré, par exemple constitué de triangles isocèles ou de carrés juxtaposés de même taille pour un problème à deux dimensions (figure 2), la seconde condition est facilement remplie.
Cependant de type de maillage pose également des problèmes :
- il permet difficilement de représenter des ouvrages dont la géométrie est compliquée (première condition) ;
- la taille des cellules est obligatoirement la même partout ce qui, soit limite la précision du maillage, soit conduit à un très grand nombre de cellules.
Nota : Dans le cas d'un maillage structuré rectangulaire il est cependant possible d'utiliser des cellules de taille différente à condition que le rapport des dimensions entre deux cellules contiguës soit dans un rapport de 2 (maillage Cutcell).
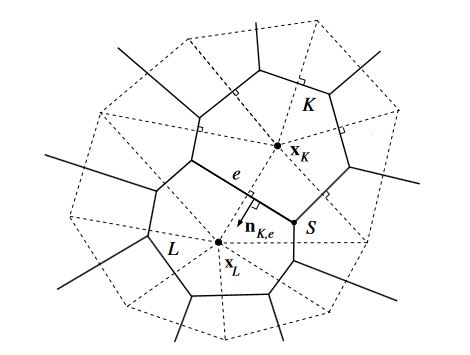
On utilise donc souvent des maillages structurés dans les zones internes de l’écoulement et non structurés en proche paroi en utilisant des procédés de construction spécifiques, par exemple triangulation de Delaunay ou polygones de Voronoï (Scheid, 2017) (figure 3).
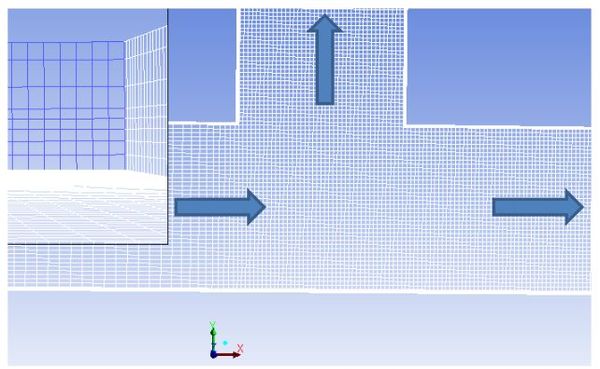
Dans la pratique les logiciels sont généralement dotés de fonctions spécifiques (mailleurs) permettant de construire le maillage de façon assistée. Cette étape reste cependant très délicate car elle nécessite de trouver un équilibre entre la précision attendue et le temps de calcul. Comme indiqué précédemment ce compromis impose généralement de densifier le maillage dans les zones où les grandeurs évoluent rapidement (ce qui suppose que l'on a une idée a priori de l'allure du phénomène) (figure 4).
La qualité du maillage est une étape importante à considérer afin de permettre une convergence des équations à résoudre. Plusieurs métriques sont classiquement utilisées pour qualifier un maillage : Aspect Ratio, Non-orthogonality, Volume Ratio, Skewness entre autres.
Domaines d'utilisation en hydrologie et en hydraulique
Les systèmes d'assainissement sont très étendus et constitués d'un grand nombre d'ouvrages. Leur représentation complète par des outils de MFN nécessiterait des capacités de calcul qui sont encore, et sans doute pour longtemps, très supérieures à celle que l'on est capable de mobiliser, que ce soit en taille mémoire (nombre de mailles nécessaires) ou en temps calcul. En effet, comme déjà indiqué, pour les écoulements à surface libre, la difficulté principale est la détermination claire et précise de la ligne d'eau, c'est à dire de la séparation entre les fluides eau et air. Cette détermination nécessite une grande finesse du maillage.
Ces contraintes sont le plus souvent également vraies dans la plupart des systèmes hydrologiques, qu'ils soient naturels ou aménagés.
L'utilisation de ces outils est cependant en développement rapide pour représenter des ouvrages spécifiques ou des phénomènes localisés. Cette partie non exhaustive a pour but d'illustrer par des exemples différents domaines d'utilisation que l’on rencontre régulièrement en hydraulique.
Modélisation d’un écoulement turbulent à surface libre non miscible : Exemple d’un déversoir d’orage
Les déversoirs d’orage font sans doute partie des ouvrages présents dans les réseaux d'assainissement et pour lesquels les apports de la MFN sont les plus utiles. Ces ouvrages jouent en effet un rôle très importants dans le fonctionnement des réseaux en conditionnant les rejets urbains de temps de pluie et leur fonctionnement hydraulique, souvent compliqué, est très mal représenté par les méthodes classiques de simulation (en général équations de Barré de saint venant).
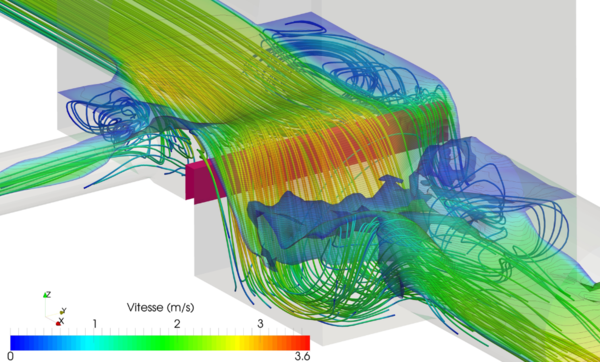
L'exemple suivant (figure 5) illustre la simulation d'un déversoir frontal fonctionnant en régime fluvial à l'amont et en régime torrentiel à l'aval de façon à mieux contrôler les débits conservés. La modélisation hydrodynamique permet de vérifier le bon fonctionnement de ce type d’ouvrage pour les sollicitations les plus fortes (période de retour de 10 ans par exemple).
L'utilisation de modèles de MFN pour représenter ce type d'ouvrages permet d'évaluer les incertitudes associées aux représentations classiques et éventuellement de proposer des modélisations simplifiées alternatives.
Nota : Une utilisation particulière des outils de MFN pour ce type d'ouvrage (qui doivent être instrumentés dans le cadre de l'autosurveillance) est l'optimisation du positionnement des sondes. Les capteurs les plus performants sont en effet les capteurs de niveau. Le calcul du débit déversé connaissant la hauteur d'eau s'effectue ensuite en appliquant une loi de seuil. La difficulté réside dans le fait que la ligne d'eau le long du seuil peut être très variable et très perturbée. Si le capteur n'est pas installé au bon endroit sa mesure peut ne pas être représentative de la forme réelle de la ligne d'eau et les calculs de débit sont alors entachés d'une grande incertitude. L'utilisation d'outils de CFD permet de choisir de façon efficace la meilleure position des sondes et de paramétrer correctement la loi de seuil (Mignot et al, 2011).
Représentation des ouvrages de stockage-décantation
On installe de plus en plus souvent des bassins de stockage dans les systèmes d'assainissement. Ces ouvrages peuvent avoir une fonction strictement hydraulique (laminage des crues) ou une fonction de traitement (favoriser la décantation des particules et des polluants associés). Quel que soit leur objectif une bonne maîtrise des phénomènes de dépôt et de reprise est indispensable pour contrôler la décantation, que ce soit pour l'éviter (cas de ouvrages hydrauliques) ou la favoriser (cas des ouvrages de traitement).
La représentation numérique de ces phénomènes avec les outils de MFN s'effectue en utilisant une représentation bi ou tri-dimensionnel des écoulements dans l'ouvrage et en couplant les équations régissant l'écoulement avec celles régissant le transport solide. Un bon calage des conditions de reprise des particules déposées permet de très bien représenter les différents phénomènes (figure 6).
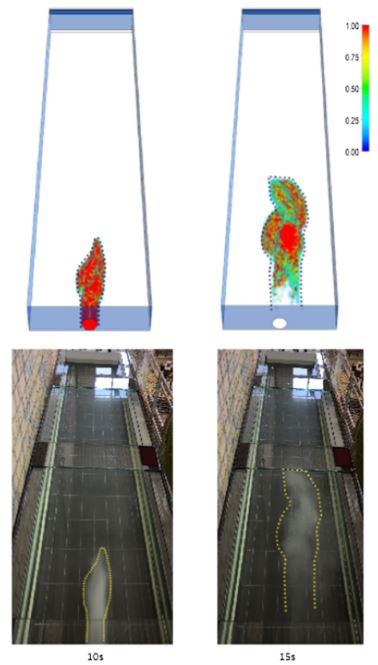
L'utilisation des outils de MFN permet en particulier de bien définir la géométrie d'ouvrage la mieux adaptée en fonction des attentes. Elle permet en effet de tester rapidement des géométries différentes (forme du bassin, position des entrées et ds sorties, utilisation éventuelle de déflecteur, etc.). (Yan et al, 2020)
Bibliographie :
- Lipeme Kouyi, G. (2022) : Modélisation CFD des écoulements dans les ouvrages spéciaux: déversoirs, bifurcations et bassins ; cours d'hydraulique, INSA Lyon, dpt GCU.
- Mignot, E., Bonakdari, H., Knothe, P., Lipeme Kouyi, G., Bessette, A., Rivière, N., Bertrand-Krajewski, J.L. (2011) : Experiments and 3D simulations of flow structures in junctions and of their influence on location of flowmeters ; 12th International Conference on Urban Drainage, Porto Alegre/Brazil, 11-16 September 2011 ; 9p. ; disponible sur https://www.researchgate.net
- Monplot, A. (2014) : Modélisation tridimensionnelle des écoulements en réseau d’assainissement ; Évaluation des modèles RANS à travers l’étude des écoulements au droit d’ouvrages spéciaux ; thèse de doctorat INSA de Lyon ; 206p. ; disponible sur https://www.theses.fr/2014ISAL0125.pdf.
- Scheid, J.-F. (2017) : Volumes finis ; Méthodes numériques avancées pour la résolution des EDP ; cours de Master 2 ; IMOI, Université de Lorraine ; 67p. ; disponible sur http://scheid.perso.math.cnrs.fr/Enseignement/polyVF2017_18.pdf.
- Yan, H., Vosswinkel, N., Ebbert, S., Lipeme Kouyi, G., Mohn, R., (2020) : Numerical investigation of particles’ transport, deposition and resuspension under unsteady conditions in constructed stormwater ponds ; Environmental Sciences Europe, 2020, 32 (76) ; 17p. ; disponible sur https://enveurope.springeropen.com
Pour en savoir plus :
- Aksouh, M., Mataoui, A. (non daté) : Travaux pratiques de mécanique des fluides numériques ; cours de master INSA Lyon, LMFTA ; 45p. ; disponible sur https://www.scribd.com/document
 S'abonner à un flux RSS
S'abonner à un flux RSS