Utilisateur:Jean-Michel Tanguy/SujetENTPE2023/B33 : Différence entre versions
(→Cas n°1) |
(→Cas n°1) |
||
| Ligne 97 : | Ligne 97 : | ||
*<span style="color:crimson">''' Étude de sensibilité '''</span> | *<span style="color:crimson">''' Étude de sensibilité '''</span> | ||
| − | [[Fichier:etude_k3.png| | + | [[Fichier:etude_k0.png|400px]] |
| + | [[Fichier:etude_k1.png|400px]] | ||
| + | [[Fichier:etude_k2.png|400px]] | ||
| + | [[Fichier:etude_k3.png|400px]] | ||
== <span style="color:seagreen">Cas n°2</span> == | == <span style="color:seagreen">Cas n°2</span> == | ||
Version du 8 juin 2023 à 15:41
Sommaire |
Contexte
Modèle de Berkhoff et résolution analytique
Résolution par homotopie
Étude des différents cas
Cas n°1
On étudie le cas du canal monodimensionnel plat de longueur L.
On suppose une entrée par l’aval ( en $ x=0 $) d’une onde qui vérifie la condition de Dirichlet donc de fréquence unitaire $ \phi(x=0)=1 $ et une sortie libre en amont (en $ x=L $) qui vérifie la condition de Robin $ \phi_x(x=L)=ik\phi(x=L) $.
- Résolution analytique
Comme vu précédemment l’équation du modèle de Berkhoff en 1D devient alors l'équation différentielle du deuxième ordre suivante :
$ \phi_{xx}+k^2\phi=0 $
On a alors pour solution: $ \phi(x)={K_1}e^{ikx}+{K_2}e^{-ikx} $ avec $ ({K_1},{K_2}) \in \mathbb{C^2} $
Avec les conditions aux limites imposées on obtient,
$ \phi(x=0)=K_1+K_2=1 \Rightarrow K_2= 1-K_1 $
$ \phi_x(x=L)=ik\phi(x=L) $ $ \Rightarrow {ik}({K_1}e^{ikL}-{K_2}e^{-ikL}) = {ik}({K_1}e^{ikx} + {K_2}e^{-ikx}) $
Donc $ K_2 =0 $ et $ K_1=1 $
On obtient alors une première solution, $ \phi(x)=e^{ikx} $
Le potentiel est la partie réelle donc
$ \phi(x)=cos(kx) $
- Résolution par homotopie
La relation d'homotopie s'écrit en choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle:
$ (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $
En injectant la décomposition en série entière $ \phi(x,p)=\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+p^3\phi_3(x)+... $ et sa seconde dérivée:
$ \phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+... $
Nous obtenons:
$ (1-p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+p^3\phi_3(x)+...)]=0 $
Il faut ensuite simplifier et écrire cette relation suivant les puissances de p croissantes. Cette relation étant valable quel que soit p, tous les coefficients devant les puissances de p sont donc nuls.
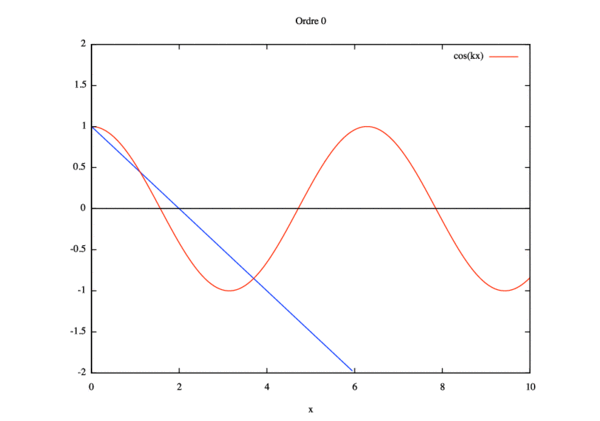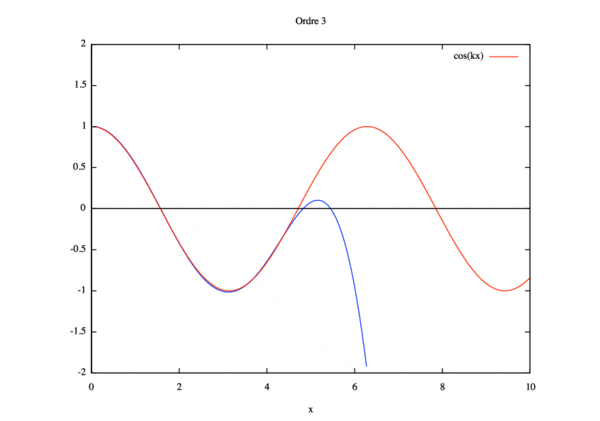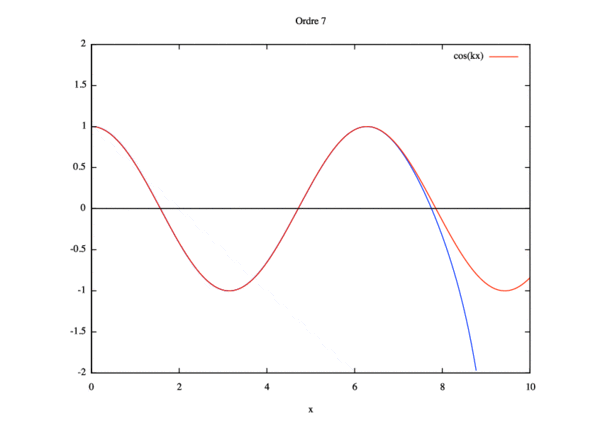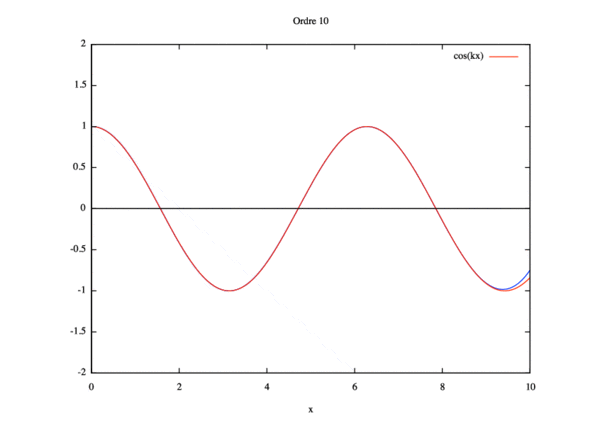
- Ordre 0 :
$ \phi_{0,xx}=0 $ soit $ \phi_0=Ax+B $.
Introduisant les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, il vient :
$ B=0 $
$ A= ik(AL+1) \Rightarrow A = \dfrac{ik}{1-ik} $
Donc
$ \phi_0(x)=1+\dfrac{ik}{1-ikL}x $
- Ordre 1 :
$ \phi_{1,xx}-\phi_{0,xx}+\phi_{0,xx}+k^2\phi_0=0 $ soit $ \phi_{1}=-k^2\int\phi_0dxdx +Ax+B $.
Introduisant les conditions limites suivantes: $ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $, il vient :
$ \phi_1(x)=- \dfrac{k^2L(k^2L^2+3ikL-3)} {3(1-ikL)^2}x-k^2\left (\dfrac{ik} {6(1-ikL)}x^3+\dfrac{1} {2}x^2 \right ) $
- Ordre 2 :
$ p^2 \phi_{2xx}(x)-p^2\phi_{1xx} + p^2\phi_{1xx} +k^2p^2\phi_{1xx} = 0 $
d'où $ \phi_{2xx}(x)=-k^2\phi_{1xx} $
Alors
$ \phi_{2}(x)= -k^2 \iint{\phi_1(x)dxdx} + Ax + B $
$ k=\dfrac{1} {100} $ (nombre d'onde en m-1), $ H=40 $ (profondeur en m), $ c=\sqrt{gH} $ (célérité de l'onde en m/s), $ \lambda=\dfrac{2\pi}{k} $ (longueur d'onde en m), $ L=2\lambda $ (longueur du domaine en m).
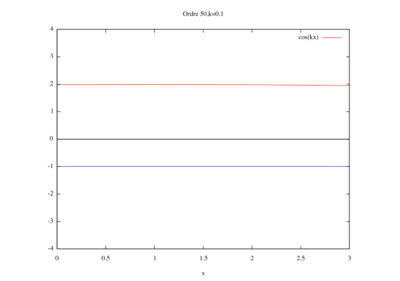
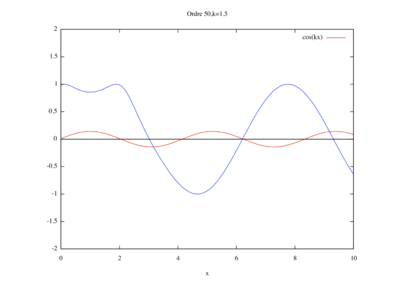
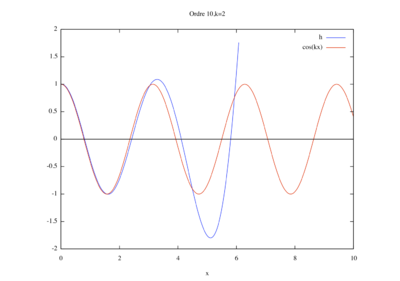
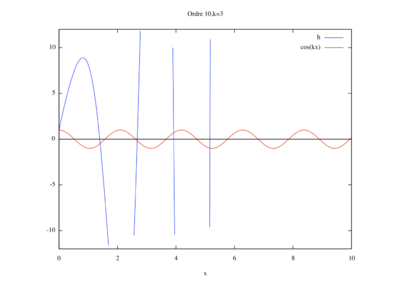
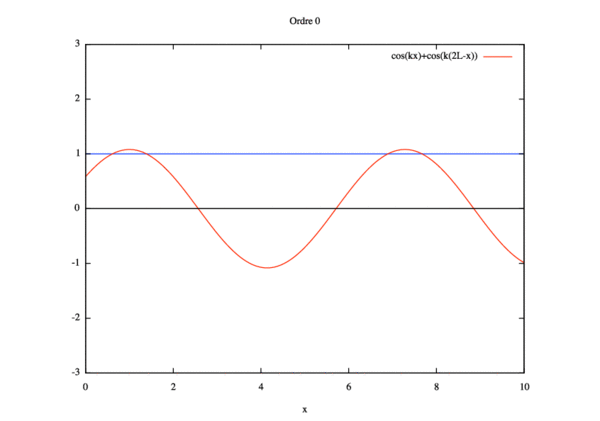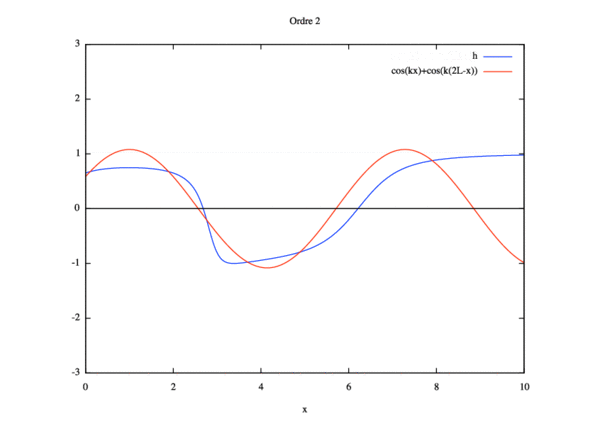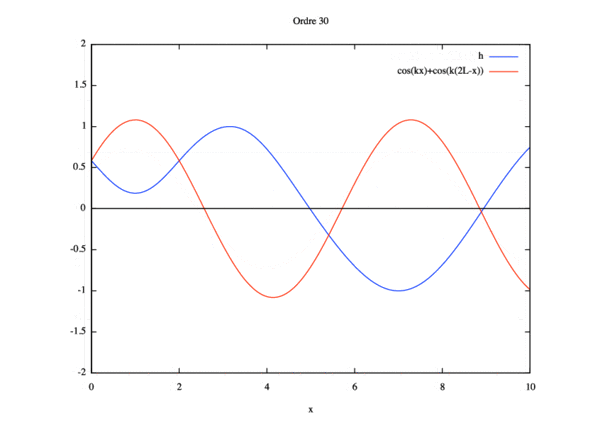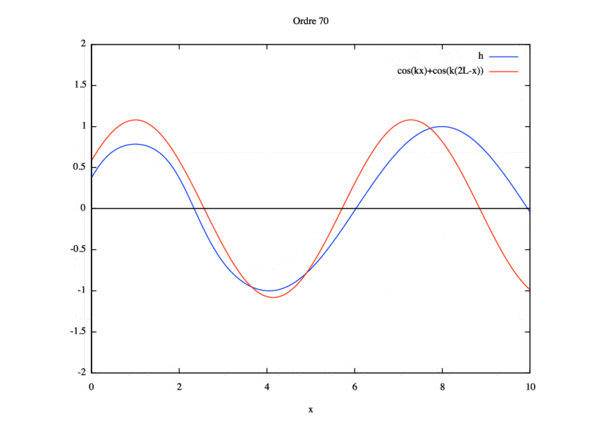
- Étude de sensibilité
Cas n°2
On étudie un canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ \phi_x=ik(2-\phi) $ et réflexion totale amont $ \phi_x=0 $ .
- Résolution analytique
On obtient la même équation du modèle de Berkhoff vue dans le cas n°1,
$ \phi_{xx}+k^2\phi=0 $
$ \Rightarrow \phi(x)={K_1}e^{ikx}+{K_2}e^{-ikx} $ avec $ ({K_1},{K_2}) \in \mathbb{C^2} $
Seules les conditions aux limites changent,
$ \phi_x(x=0)=ikK_1 - ikK_2= ik(2-\phi(x=0)) \Rightarrow K_1-K_2= 2-K_1-K_2 \Rightarrow 2K_1=2 \Rightarrow K_1 =1 $
$ \phi_x(x=L)=0 \Rightarrow {ik}({K_1}e^{ikL}-{K_2}e^{-ikL}) = 0 \Rightarrow e^{ikL} - K_2e^{-ikL} =0 \Rightarrow K_2= e^{i2kL} $
d'où $ \phi(x) = e^{ikx} + e^{ik(2L-x)} $
Le potentiel est la partie réelle
$ \phi(x)= cos(kx)+ cos(k(2L-x)) $
- Résolution par homotopie
$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+...)]=0 $
- Ordre 0 :
$ \phi_{0,xx}(x)=0 $
En intégrant on obtient $ \phi_0(x)=Ax+B $
Avec les conditions aux limites : $ \phi_{0,x}^0=ik(2-\phi) $ et $ \phi_{0, x}^L=0 \Rightarrow A = 0 $ et $ B = 2 $
Donc
$ \phi_0(x)=2 $
- Ordre 1 :
$ \phi_{1,xx}(x) = -k^{2}\phi_0(x) \Rightarrow \phi_1 (x) =- k^2x^2 + Ax + B $
Avec les conditions initiales données on a $ A = 2k^2L $ et $ B = 2ikL $ et donc :
$ \phi_1 (x) = - k^2x^2 + 2k^2Lx + 2ikL $
Cas n°3
On étudie un canal monodimensionnel de longueur L avec pente du fond constante (s=cste) avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $ et sortie libre amont $ \phi_x=ik\phi $.
- Résolution analytique
Cas $ k = k_0 \sqrt{\dfrac{H_0}{H(x)}} $
On a $ C=C_g = \sqrt{gH(x)} $
Le modèle de Berkhoff devient alors
$ \nabla (gH(x) \nabla \phi ) + {k}^{2}gH(x)\phi = 0 \Leftrightarrow H(x) \Delta \phi - s \vec{grad} \phi + {k}^{2}H(x)\phi = 0 $
On réalise un changement de variable $ z = H_{0} -sx $
On obtient alors
$ \phi_{xx} - \dfrac{s}{H_0-sx}\phi_x +\dfrac{k_0^2}{H_0-sx}\phi = 0 $
d'où l'équation de type Bessel suivante :
$ z\phi_{zz} + \phi_z + {\alpha}^{2}\phi = 0 $
avec $ \alpha^{2} =\dfrac{{k_0}^{2}H_{0}}{s^2}, \frac{\partial \phi}{\partial x} = -s\phi_{z} $ et $ \frac{\partial^2 \phi}{\partial x^2} = s^2\phi_{zz} $
La solution est de la forme $ \phi(z) = [K_1J_0(2\alpha\sqrt{z})+K_2Y_0(2\alpha\sqrt{z})] $
Avec les conditions aux limites on a :
$ \phi(0)=1 \Leftrightarrow [K_1J_0(2\alpha\sqrt{H_0})+K_2Y_0(2\alpha\sqrt{H_0})] = 1 $
$ \phi_z(L) = ik \phi(L) $
En notant la dérivée première de $ J_0, J_1 $ et la celle de$ Y_0, Y_1 $ , on obtient
$ \phi_z(L) = \dfrac{\alpha s }{\sqrt{H_0-sL}} [K_1 J_1(2\alpha\sqrt{H_0-sL})+K_2Y_1(2\alpha\sqrt{H_0-sL})] = ik[K_1J_0(2\alpha\sqrt{H_0-sL})+K_2Y_0(2\alpha\sqrt{H_0-sL})] $
Il faut alors déterminer $ K_1 $ et $ K_2 $ :
On note alors $ J_0^0 = J_0(2\alpha\sqrt{H_0}), J_0^L = J_0(2\alpha\sqrt{H_0-sL}), Y_0^0= Y_0(2\alpha\sqrt{H_0}), Y_0^L = Y_0(2\alpha\sqrt{H_0-sL}) $ et de même pour $ J_1^0, J_1^L, Y_1^0, Y_1^L, $...
On a alors
$ K_1 = \dfrac{Y_1^L-iY_0^L}{ J_0^0 (Y_1^L -iY_0^L) + Y_0^0 (iJ_0^L- J_1^L)} $
et
$ K_2 = \dfrac{ iJ_0^L - J_1^L}{ J_0^0 (Y_1^L -iY_0^L) + Y_0^0 (iJ_0^L- J_1^L)} $
donc
$ \phi(z) = \dfrac{Y_1^L-iY_0^L}{ J_0^0 (Y_1^L -iY_0^L) + Y_0^0 (iJ_0^L- J_1^L)} J_0(2\alpha\sqrt{z}) + \dfrac{ iJ_0^L - J_1^L}{ J_0^0 (Y_1^L -iY_0^L) + Y_0^0 (iJ_0^L- J_1^L)} Y_0(2\alpha\sqrt{z}) $
- Résolution par homotopie
Toujours avec $ k = k_0 \sqrt{\dfrac{H_0}{H(x)}} $, on utilise la relation de Berkhoff obtenue précédemment pour établir la relation d'homotopie de la même manière que dans les cas précédents :
$ (1-p) \phi_{xx} + p[(H_0 -sx) \phi_{xx} -s\phi_{x} + k_0^2 H_0\phi] = 0 $
En injectant la décomposition en série entière de $ \phi(x,p), \phi_x(x,p), \phi_{xx}(x,p) $, on obtient :
$ (1-p) [\phi_{0,xx} +p \phi_{1,xx} + p^2 \phi_{2,xx} + ...] + p[(H_0 - sx)(\phi_{0,xx} +p \phi_{1,xx} + p^2 \phi_{2,xx} + ...) - s (\phi_{0,x} +p \phi_{1,x} + p^2 \phi_{2,x} + ... ) + {k_0}^{2}{H_0} (\phi_0 + p\phi_1 +p^2\phi_2+...)] $
- Ordre 0 :
$ \phi_{0,xx} = 0 \Leftrightarrow \phi_0 = Ax + B $
or $ \phi_0(0) = B = 1 $ et $ \phi_{0,x}(L) = ik(AL+B) = A \Leftrightarrow A = \dfrac{ik}{1-ikL} $ , d'où
$ \phi_0 (x) = \dfrac{ik}{1-ikL}x + 1 $
- Ordre 1 :
$ \phi_{1,xx} + (H_0-sx - 1 )\phi_{0,xx} - s \phi_{0,x} + k_0^2H_0 \phi_0 = 0 $
$ \Rightarrow \phi_{1,xx} = - (H_0-sx - 1 )\phi_{0,xx} + s \phi_{0,x} - k_0^2H_0 \phi_0 $
$ \Rightarrow \phi_{1,xx} = s \dfrac{ik}{1-ikL} - k_0^2H_0 ( \dfrac{ik}{1-ikL}x + 1 ) $
$ \Rightarrow \phi_{1,x} = s \dfrac{ik}{1-ikL}x - k_0^2H_0 \dfrac{ik}{1-ikL} \dfrac {x^2}{2} - k_0^2H_0 x + A $
$ \Rightarrow \phi_1 = s \dfrac{ik}{1-ikL}\dfrac{x^2}{2} - k_0^2H_0 \dfrac{ik}{1-ikL} \dfrac{x^3}{6} - k_0^2H_0\dfrac{x^2}{2} + Ax + B $
Avec les conditions initiales on obtient :
$ \phi_(0)= 0 \Rightarrow B = 0 $
et
$ \phi_{1,x}(L) = ik\phi_1(L) $
$ \Rightarrow A(1-ikL) = - \dfrac{sk}{1-ikL}(\dfrac{ikL^2}{2}-L) + k_0^2H_0 \dfrac{ik}{1-ikL}(\dfrac{L^2}{2} - \dfrac{ikL^3}{6}) + k_0^2H_0L(1-\dfrac{ik}{2}) $
$ \Rightarrow A= \dfrac{iksL}{(1-ikL)^2}(\dfrac{ikL}{2}-1) + \dfrac{k_0^2H_0L}{1-ikL}(1 - \dfrac{ik}{2}+\dfrac{ikL}{2(1-ikL)} + \dfrac{k^2L^2}{6(1-ikL)}) $
d'où
$ \phi_1(x) = s \dfrac{ik}{1-ikL}\dfrac{x^2}{2} + k_0^2H_0 \dfrac{ik}{1-ikL} \dfrac{x^3}{6} + k_0^2H_0\dfrac{x^2}{2} + \dfrac{iksL}{(1-ikL)^2}(\dfrac{ikL}{2}-1) + \dfrac{k_0^2H_0L}{1-ikL}(1 - \dfrac{ik}{2}+\dfrac{ikL}{2(1-ikL)} + \dfrac{k^2L^2}{6(1-ikL)})x $
Cas n°4
On considère une vague sphérique générée par une source périodique sinusoïdale.
Nous traitons ici de l'évolution de la surface libre dans un domaine infini en grande profondeur. La source ponctuelle est appliquée autour d'un cercle de rayon r_0 centré sur un domaine circulaire de rayon R qui laisse sortir librement cette onde en r=R.
L'équation de Berkhoff se simplifie alors en équation de Helmholtz et s'exprime en coordonnées polaires avec les conditions suivantes:
$ \begin{cases} \Delta \phi + k^2\phi=0, \\ \phi(r-r_0)=1, \\\phi_r(r=R)=ik\phi(r=R). \end{cases} $
En coordonnées polaires, la relation ci-dessus s'écrit de manière simplifiée étant donné que le problème est caractérisé par une symétrie de révolution, donc est indépendant de $ \theta $.
$ \begin{cases} \phi_{rr}+\dfrac{1}{r}\phi_r + k^2\phi=0, \\ \phi^{r=r_0}=1, \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases} $
- Résolution analytique
La solution de cette équation est de la forme $ \phi(r) = K_1 J_0(kr) + K_2 Y_0(kr) $
Avec les conditions initiales on a :
$ \phi (r=r_0) = K_1 J_0^{0} + K_2 Y_0^{0} = 1 $ avec $ J_0^{0} = J_0(kr_0) $ et $ Y_0^{0} = Y_0(kr_0) $
$ \phi_r(r) = k(K_1 J_1^r + K_2 Y_1^r) $ avec $ J_1^r= J_0' (kr) $ et $ Y_1^r =Y_0'(kr) $
$ \Rightarrow \phi_r(R) = k(K_1 J_1^R + K_2 Y_1^R) = ik (K_1 J_0^R+ K_2 Y_0^R) $
d'où
$ K_1 = \dfrac{Y_1^R -iY_0^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)} $
et
$ K_2 = \dfrac {iJ_0^R - J_1^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)} $
donc
$ \phi(r) = \dfrac{Y_1^R -iY_0^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)}J_0(kr) + \dfrac {iJ_0^R - J_1^R}{J_0^0(Y_1^R-iY_0^R) + Y_0^0(iJ_0^R -J_1^R)} Y_0(kr) $
- Résolution par homotopie
En coordonnées polaires, la relation d'homologie devient : $ (1-p) \phi_{rr} + p(\phi_{rr}+ \dfrac{1}{r} \phi_r + k^2\phi) = 0 $
En décomposant en série entière $ \phi(r) $, $ \phi_r(r) $ et $ \phi_{rr}(r) $ on obtient :
$ (1-p) [\phi_{0,rr} + p\phi_{1,rr} +p^2\phi_{2,rr} + ...] + p[\phi_{0,rr} + p\phi_{1,rr} +p^2\phi_{2,rr} + ...+ \dfrac{1}{r} (\phi_{0,r} +p\phi_{1,r} + p^2\phi_{2,r}+...) + k^2(\phi_0 + p\phi_1 +p^2\phi_2+...)] $
- Ordre 0 :
$ \phi_{0,rr} (r) = 0 \Rightarrow \phi_0(r)= Ar +B $
Avec les conditions initiales :
$ \phi_0(r_0) = Ar_0 + B =1 \Rightarrow B=1-Ar_0 $
et
$ \phi_{0,r}(R) = ik\phi_0(R) \Rightarrow A = ik(AR+B) $
d'où
$ A = \dfrac{ik}{1+ik(r_0-R)} $
et
$ B = 1 - \dfrac{ikr_0}{1+ik(r_0-R)} $
donc
$ \phi_0(r) =\dfrac{ik}{1+ik(r_0-R)}r +1 - \dfrac{ikr_0}{1+ik(r_0-R)} $
 S'abonner à un flux RSS
S'abonner à un flux RSS