S'abonner à un flux RSS
 

Transport solide de fond (HU) : Différence entre versions

De Wikhydro
(→‎Approche pratique)
(→‎Éléments de modélisation)
Ligne 91 : Ligne 91 :
  
  
−
<center><math>X = \frac{u_*.D}{ν}\qquad (3)</math></center>
+
<center><math>X = \frac{u_*.d}{ν}\qquad (3)</math></center>
  
 
et  
 
et  
  
  
−
<center><math>Y = \frac{τ_w}{g.(ρ_s-ρ).D}\qquad (4)</math></center>
+
<center><math>Y = \frac{τ_w}{g.(ρ_s-ρ).d}\qquad (4)</math></center>
  
  
 
Avec :  
 
Avec :  
 
* <math>τ_w</math> : contrainte de cisaillement près du fond ou des parois (N/m<sup>2</sup>),  
 
* <math>τ_w</math> : contrainte de cisaillement près du fond ou des parois (N/m<sup>2</sup>),  
−
* <math>D</math> : dimension caractéristique des particules (m),
+
* <math>d</math> : dimension caractéristique des particules (m),
 
* <math>ρ</math> : masse volumique du fluide (kg/m<sup>3</sup>),  
 
* <math>ρ</math> : masse volumique du fluide (kg/m<sup>3</sup>),  
 
* <math>ρ_s</math> : masse volumique des particules (kg/m<sup>3</sup>),  
 
* <math>ρ_s</math> : masse volumique des particules (kg/m<sup>3</sup>),  
Ligne 115 : Ligne 115 :
 
.
 
.
  
−
En remplaçant τ_w par sa valeur, la variable Y peut donc s'écrire :
+
En remplaçant <math>τ_w</math> par sa valeur, la variable <math>Y</math> devient :
  
  
−
<center><math>Y = \frac{ρ.u_*^2}{g.(ρ_s-ρ.D}\qquad (6)</math></center>
+
<center><math>Y = \frac{ρ.u_*^2}{g.(ρ_s-ρ).d}\qquad (6)</math></center>
 
   
 
   
  
 +
Il est donc possible d'écrire <math>Y</math> en fonction de <math>X</math> :
  
−
Y peut s’écrire selon  Y=〖u*〗^2/(ρs/ρ  -1)gD=((u* .D)/υ)^2 ((ρυ^2)/((ρs/ρ  -1)g.D^3 ))
 
  
−
Ce qui, pour des valeurs de ρs de ρ et de υ constantes se simplifie sous la forme :
+
<center><math>Y = (\frac{u_*.d}{ν})^2.\frac{ρ.ν^2}{g.(ρ_s-ρ).d^3}\qquad (7)</math></center>
 +
 
 +
 
 +
Ce qui, pour des valeurs de <math>ρ_s</math>, de <math>ρ</math> et de <math>υ</math> constantes se simplifie sous la forme :
 +
 
 +
 
 +
<center><math>Y = C.\frac{X^2}{D^3}\qquad (8)</math> <center>
 +
 
 +
 
 +
Avec la constante C égale à :
 +
 
  
−
Y = X 2.cte/D3
 
  
 
Pour chaque valeur de u* donc de √(g.Rh.J), X et Y définissent un point dans le plan de Shields. Quand (Rh.J) varie, ce point décrit une parabole qui coupe la courbe de Shields au point correspondant au début d'entraînement ou au maintien au repos.
 
Pour chaque valeur de u* donc de √(g.Rh.J), X et Y définissent un point dans le plan de Shields. Quand (Rh.J) varie, ce point décrit une parabole qui coupe la courbe de Shields au point correspondant au début d'entraînement ou au maintien au repos.

Version du 28 février 2024 à 16:23

Traduction anglaise : Bedload transport

article en chantier

Dernière mise à jour : 28/02/2024

Part du transport solide qui est effectué près du fond (saltation) ou en contact avec le fond (charriage) (figure 1).

Sommaire

Éléments de base

Le transport de fond concerne les matériaux les plus grossiers et les plus denses qui sont transportés sur le fond des cours d’eau, ou, en assainissement, près du radier des collecteurs et conduites.


Figure 1 : Les deux formes de transport de fond : charriage en haut et saltation en bas ; le passage d'un mode à l'autre peut être très chaotique.

Le transport de fond joue un rôle très important dans l'évolution géomorphologique des cours d'eau naturels (voir Morphodynamique (HU)). Les lits fluviaux sont en effet des enveloppes mobiles régulées par des processus de dépôt et d’érosion qui résultent eux-mêmes de la recherche d’un équilibre dynamique entre les flux sédimentaires et les flux hydriques. Un tronçon de cours d’eau sera stable si sa capacité de transport solide, contrôlée par le débit liquide de crue et la pente, est exactement compensée par la dissipation d’énergie occasionnée par le transport de la charge solide et la taille des sédiments. Ce sont généralement les matériaux les plus grossiers qui assurent cette stabilité.

Cependant, dans cet article nous traiterons principalement de la question du transport de fond dans les collecteurs d'assainissement qui a pour particularité de se produire sur un fond fixe, et particulièrement le cas des réseaux unitaires qui posent les problèmes les plus difficiles.

Description du phénomène dans les réseaux d'assainissement

Éléments d'observation

Il a été possible d'analyser les matériaux se déplaçant près du fond dans quelques égouts unitaires (Laplace, 1991 ; Bachoc, 1992). Il existe cependant de nombreuses difficultés pour évaluer la contrainte de cisaillement de même que pour mesurer précisément la vitesse de chute des particules.

Une proportion importante de la masse du transport de fond est composée de matériau granulaire inorganique, ayant une forte masse volumique. Ce sont ces matériaux qui sont responsables de la plupart des problèmes de maintenance des égouts car ce sont ceux qui se déposent en premier. Lorsque ces solides sont arrêtés par une cause quelconque, souvent au niveau d’une singularité hydraulique mais aussi lorsque la baisse subite des débits de temps de pluie les a "laissés là", ils ont une forte tendance à s'accumuler.

La proportion de matière organique dans les solides transportés sur le fond est moins forte dans les réseaux pluviaux que dans les unitaires, et dans ceux-ci elle semble plus forte lorsque la vitesse des eaux de temps sec est faible. Dans certains cas, le matériau se déplaçant près du fond (qu'il y ait ou non un dépôt sur le fond) peut être relativement granulaire, c'est à dire voisin de celui que l'on trouve usuellement dans les rivières. Différentes études (Ahyerre, 1999 ; Bébin & al, 1993) ont montré que si la pente était forte (> 2%) le transport de fond était essentiellement constitué de particules grossières (2 à 10 mm), alors que si la pente était faible (< 0,1%), la granulométrie des particules était voisine de celle des particules transportées en suspension.

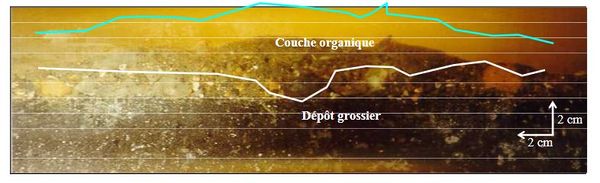
On a également observé dans certains grands collecteurs unitaires la présence de grosses particules (> 1mm), très organiques formant une couche juste au dessus du lit (Oms, 2003). Des contraintes de cisaillement de l'ordre de 1 N/m2 sont suffisantes pour entraîner ces particules. Les concentrations en solide sont très fortes dans cette couche particulière, puisque l'on a pu observer des concentrations supérieures à 3 500 mg/L (à comparer aux valeurs habituellement trouvées en suspension qui sont de l'ordre de 200 à 500 mg/L). Les concentrations en polluants y sont également extrêmement élevées (Ahyerre, 1999). Ce fluide très dense, mélange de liquide et de solide est probablement non-Newtonien et pourrait avoir les caractéristiques d'un fluide de Bingham. On parle parfois de couche organique de fond (figure 2). Il est possible que certaines similitudes existent avec les bouchons vaseux que l'on observe dans certains estuaires, bien que ces derniers sous-écoulements soient plus homogènes et aient des concentrations plus fortes en solides (>10g/L).


Figure 2 : Vue en coupe de la couche organique de fond à l’interface eau-sédiment ; Source : Ahyerre (1999).

On a tenté de modéliser ce sous-écoulement dense en faisant l'hypothèse de l'existence d'une zone dite de suspension intérieure située près du lit et contenant des particules relativement grandes (> 0.5mm), organiques (contenu organique > 90%), peu en contact avec le lit, et emprisonnées dans une sorte de matrice d'écoulement en suspension. Le mouvement dans cette couche est supposé dépendre de la migration de particules (due aux contraintes de cisaillement) depuis les zones où le cisaillement est fort vers celles où le cisaillement est plus faible. Comme il existe un gradient vertical très marqué de vitesse à proximité immédiate du lit, les plus grandes particules seraient les plus enclines à émigrer loin du lit car elles sont assez grandes pour que leurs bords inférieurs et supérieurs soient soumis à des vitesses sensiblement différentes. Les faibles contraintes de cisaillement suffisantes pour remettre en mouvement ce matériau. Cela suggère qu'il pourrait constituer une composante importante du caractère organique des matières en suspension dans les eaux de temps de pluie, plus marqué au sein des réseaux unitaires qu’au sein des réseaux pluviaux relativement stricts, avec une contribution quantitative plus importante que celle de l'érosion des films biologiques (également chargés en matière organique) qui se forment sur les parois des conduites.

On trouvera une excellente synthèse des connaissances sur les solides en réseau dans Ashley et al. (2004).

Éléments de modélisation

Transport en suspension et transport de fond

Dans les écoulements chargés en sédiments, il existe un processus continu d'échanges entre les particules en mouvement et les particules provisoirement sédimentées, et, concernant celles qui sont en mouvement entre les particules qui sont en suspension, celles qui sont transportées sur le fond et celles qui sont transportées près du fond. Les caractéristiques de ces particules sont également susceptibles de se modifier du fait de différents phénomènes : floculation, agglutination, agrégation, dégradation et processus biologiques.

Une distinction importante peut cependant être faite entre le transport en suspension et le transport de fond, comprenant la saltation et les déplacements liés à des rotations ou à des glissades sur le fond (charriage). Dans l'état actuel des connaissances, il reste des incertitudes sur la nature des matériaux qui se déplacent près du fond dans les systèmes unitaires d'assainissement. Malgré tout, on pense généralement que les concepts développés en hydraulique fluviale peuvent être appliqués. Les particules transportées sur le fond sont caractérisées par le fait qu'elles ne reçoivent aucune impulsion verticale dirigée vers le haut autre que celles dues aux contacts successifs avec le fond, ces impulsions étant elles-mêmes essentiellement horizontales. Il est maintenant bien admis que la saltation, qui constitue le mode de transport principal près du fond, se produit même si l'écoulement est laminaire, c'est à dire même s'il n'y a aucune turbulence pour faciliter le transport solide. Le critère classique permettant de caractériser la transition entre transport en suspension et transport de fond, est fondé sur le paramètre de sédimentation $ η $ :


$ η = \frac{w_s}{K.u_*} $


Avec :

  • $ w_s $ : vitesse de chute de la particule (m/s) ;
  • $ K $ : constante de Von Karman ;
  • $ u_* $ : Vitesse de frottement (m/s).

Le transport de fond commence pour des valeurs de $ η $ comprises entre 5 et 15.

Critères de mise en mouvement des particules

Toute particule solide posée sur le fond sera théoriquement mise en mouvement dès que la contrainte de cisaillement, $ τ_w $, deviendra supérieure à une contrainte critique, $ τ_* $, appelée contrainte critique d'entrainement ou seuil de cisaillement. Ce seuil de cisaillement dépend d'une dimension représentative ($ d $) des particules ou, plus généralement, représentative de leur population (par exemple le diamètre médian $ D50 $), ainsi que de leur poids déjaugé.

La contrainte de cisaillement près du fond (que l'on appelle souvent contrainte de cisaillement au radier), $ τ_w $, dépend de la distribution verticale de la vitesse de l'écoulement et plus précisément de la vitesse près des parois. Moyennant certaines hypothèses, on peut approcher sa valeur dans le cas des écoulements graduellement variés (1), et de façon encore plus simple si l'on fait l'hypothèse d'un écoulement uniforme (2).


$ τ_w = ρ.g.R_h.J\qquad (1) $


$ τ_w = ρ.g.R_h.I\qquad (2) $

Avec :

  • $ τ_w $ : contrainte de cisaillement près du fond (N/m2) ;
  • $ ρ $ : masse volumique du fluide (kg/m3) ;
  • $ g $ : accélération de la pesanteur (m/s2) ;
  • $ R_h $ : rayon hydraulique de la conduite (m) ;
  • $ I $ : pente du fond (m/m).
  • $ J $ : pente de la ligne d'énergie (m/m).

Nota : On considère souvent que le seuil de mise en mouvement vaut aussi pour l’arrêt (c'est à dire le dépôt) des particules, ce qui n’est sans doute pas très faux (même si elles s’arrêtent sans doute pour des contraintes moins élevées que celles provoquant leur entraînement).

Approche pratique

Compte tenu des imprécisions liées aux forces en jeu, l’approche purement mécaniste ne s’applique qu’aux cas les plus simples. L’étude des critères de début de mise en mouvement des particules repose généralement sur une analyse dimensionnelle, calée selon des valeurs établies expérimentalement en laboratoire ou en rivière. Basée sur l’observation, la perception du seuil de début d’entrainement est soumise à l’appréciation de l’expérimentateur. Cette subjectivité introduit ici une autre forme d’imprécision (Dufresne & Isenmann, 2018).

Les valeurs moyennes étant les seules facilement accessibles à la mesure, les expérimentateurs se sont attachés à choisir des variables qui caractérisent le mieux les seuils entre repos et mouvement en considérant que le nombre de Froude et le nombre de Reynolds doivent jouer un rôle primordial (Dufresne & Isenmann, 2018 ; Lin, 1993). Cet aspect est développé dans l'article Contrainte critique d’entrainement (HU).

Dans les collecteurs les plus pentus (i.e. lorsque les matériaux sont essentiellement granulaires), le critère de Shields (Shields, 1936) permet de bien prévoir le seuil de mise en mouvement et d’arrêt des particules.

Ce diagramme a le mérite d’être adimensionnel, mais il n'est pas très facile à utiliser sous sa forme originelle. En effet, le diamètre des particules et le couple ($ R_h $ ; $ J $) interviennent dans les deux variables $ X $ et $ Y $ et de nombreux calculs itératifs sont nécessaires avant de déterminer s’il y a repos ou mouvement. De simples combinaisons de ces variables permettent d'obtenir une représentation plus pratique, comme initialement montré par Yalin (1977).

Une approche de ce type a été mise en œuvre par Laplace (1991) et Bachoc (1992) qui ont proposé de considérer les deux variables :


$ X = \frac{u_*.d}{ν}\qquad (3) $

et


$ Y = \frac{τ_w}{g.(ρ_s-ρ).d}\qquad (4) $


Avec :

  • $ τ_w $ : contrainte de cisaillement près du fond ou des parois (N/m2),
  • $ d $ : dimension caractéristique des particules (m),
  • $ ρ $ : masse volumique du fluide (kg/m3),
  • $ ρ_s $ : masse volumique des particules (kg/m3),
  • $ g $ : accélération gravitationnelle (m/s2),
  • $ u_* $ : vitesse de frottement (m/s),
  • $ μ $ : viscosité dynamique (kg/m/s).


Or il existe une relation entre la vitesse de frottement et la contrainte de cisaillement :


$ τ_w = ρ.u_*^2\qquad(5) $

.

En remplaçant $ τ_w $ par sa valeur, la variable $ Y $ devient :


$ Y = \frac{ρ.u_*^2}{g.(ρ_s-ρ).d}\qquad (6) $


Il est donc possible d'écrire $ Y $ en fonction de $ X $ :


$ Y = (\frac{u_*.d}{ν})^2.\frac{ρ.ν^2}{g.(ρ_s-ρ).d^3}\qquad (7) $


Ce qui, pour des valeurs de $ ρ_s $, de $ ρ $ et de $ υ $ constantes se simplifie sous la forme :


$ Y = C.\frac{X^2}{D^3}\qquad (8) $ <center>


Avec la constante C égale à :


Pour chaque valeur de u* donc de √(g.Rh.J), X et Y définissent un point dans le plan de Shields. Quand (Rh.J) varie, ce point décrit une parabole qui coupe la courbe de Shields au point correspondant au début d'entraînement ou au maintien au repos.

Le diagramme de Shields étant donné en coordonnées Log-Log, cette parabole devient une droite de pente égale à 2. Le point d'intersection entre cette droite et la courbe de Shields permet de déterminer la valeur de X et donc celle de (Rh.J) qui préside au début d'entraînement ou au maintien au repos des particules. Les calculs recommencés pour différentes valeurs de D permettent d’établir une relation entre (Rh.J) et D, diamètre représentatif des solides entrainés ou maintenus au repos (cf. figure 2).

Rappelons que la courbe de Shields est un lissage passant au milieu d'un nuage de points expérimentaux. Les points au dessus de la courbe représentent le début de la mise en mouvement alors que les points sous la courbe sont des particules maintenues au repos.

Compte tenu de l’opacité des écoulements en assainissement, il n’est pas possible d’observer les seuils de mise en mouvement des particules. Par contre, il est possible de prélever les solides en dépôt dans les collecteurs pour les caractériser en les considérants comme étant des solides au repos au sens de Shields. Ce raisonnement est juste tant que le débit solide reste faible c'est-à-dire tant qu’il n’influence pas les phénomènes liés au transport solide [2]. Par conséquent, pour tracer le graphique de la figure 2, la référence pour déterminer X a été prise sous la courbe de Shields, là où les solides sont maintenus au repos. Pour des valeurs constantes de ρ, g, υ et ρs, la relation entre (Rh.J) et D, diamètre représentatif des solides maintenus au repos est linéaire.


Bibliographie :

  • Ashley, R ; Bertrand-Krajewski, J.L. ; Hvitved-Jacobsen, T. ; Verbanck, M. (2004) Solids in sewers - Characteristics, effects and control of sewer solids and associated pollutants ; IWA publishing (https://www.iwapublishing.com/books/9781900222914/solids-sewers)
  • Ahyerre, M. (1999) : Bilans et mécanismes de migration de la pollution organique en réseau d'assainissement unitaire ; thèse de doctorat Paris 6.
  • Bachoc, A. (1992) : Le transfert des solides en réseaux d’assainissement unitaires ; Thèse de doctorat de l’Institut National Polytechnique de Toulouse, ENSEEIHT ; 281 p. + annexes.
  • Dufresne, M., Isenmann, G. (2018) : Transport solide ; Cours ENGEES ; 61 p.
  • Laplace, D. (1991) : Dynamique du dépôt en collecteur d’assainissement ; Thèse de doctorat de l’Institut National Polytechnique de Toulouse ; ENSEEIHT ; 202 p. + annexes.
  • Lin, H. (1993) : Le transport solide en collecteurs unitaires d’assainissement et sa modélisation ; Thèse de doctorat de l’École Nationale des Ponts et Chaussées ; 281 p. + annexes.
  • Oms, C. (2003) : Localisation, nature et dynamique de l'interface eau-sédiment en réseau d'assainissement unitaire ; Thèse de doctorat de l’Ecole Nationale des Ponts et Chaussées ; 170 p. + annexes.
  • Shields, A. (1936) : Application of Similarity Principles and Turbulence Research to Bed-Load Movement. California Institute of Technology, Pasadena (Translate from German).
  • Yalin, M.S. (1977) : Mechanics of sediment transport ; 2nd ed. Pergamon Press ; Oxford, UK. 360 pp

Pour en savoir plus :

Récupérée de « http://wikhydro.developpement-durable.gouv.fr/index.php?title=Transport_solide_de_fond_(HU)&oldid=59426 »
Outils personnels

Milieux


Territoires


Savoirs / Acteurs


Enjeux