Izzard (modèle de) (HU) : Différence entre versions
| (21 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | ''<u>Traduction anglaise</u> | + | ''<u>Traduction anglaise</u> : Izzard's model'' |
| − | [[Modèle empirique (HU)|Modèle empirique]] | + | <u>Dernière mise à jour</u> : 23/05/2024 |
| − | ( | + | |
| − | nette]] - débit à l'exutoire d'un [[Bassin versant (HU)|bassin | + | [[Modèle empirique (HU)|Modèle empirique]] proposé par Izzard (1946) pour représenter la transformation [[Pluie nette (HU)|pluie nette]] - débit à l'exutoire d'un [[Bassin versant (HU)|bassin versant]]. |
| − | versant] | + | |
== Hypothèses et formulation == | == Hypothèses et formulation == | ||
| − | Le modèle d'Izzard | + | Le modèle d'Izzard consiste à construire un [[Hydrogramme unitaire synthétique (HU)|hydrogramme unitaire synthétique]] en s'appuyant sur les éléments suivants : |
| − | + | ||
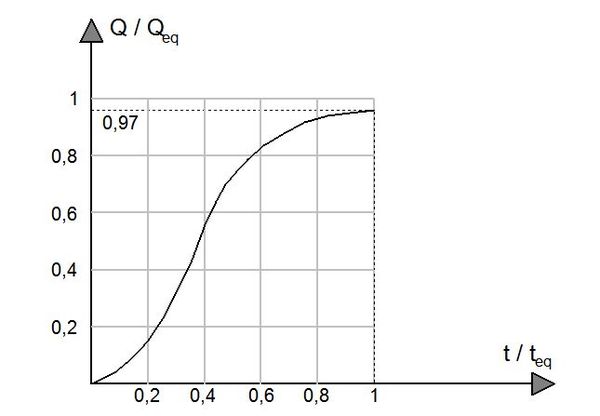
| − | * L'indépendance entre la [[Fonction de production et fonction de transfert (HU)|fonction de transfert]] et la pluie à l'origine du ruissellement (linéarité du phénomène). Cette hypothèse permet de déduire l'existence d'un [[Hydrogramme (HU)|hydrogramme]] sans dimension représentant la réponse du bassin versant à une pluie unitaire constante. Cet hydrogramme sans dimension utilise des variables normées pour les débits et les temps. Les normes sont respectivement le débit à l' | + | * L'indépendance entre la [[Fonction de production et fonction de transfert (HU)|fonction de transfert]] et la pluie à l'origine du ruissellement (linéarité du phénomène). Cette hypothèse permet de déduire l'existence d'un [[Hydrogramme (HU)|hydrogramme]] sans dimension représentant la réponse du bassin versant à une pluie unitaire constante. Cet hydrogramme sans dimension utilise des variables normées pour les débits et les temps. Les normes sont respectivement le débit à l'équilibre : <math>Q_{eq}</math> et le temps d'équilibre : <math>t_{eq}</math> (''figure 1''). |
| + | Le temps d'équilibre est défini arbitrairement comme le temps au bout duquel le débit observé devient égal à 97% du débit d'équilibre : | ||
| − | <center> | + | <center><math>Qt_{eq}= 0{,}97.Q_{eq}</math></center> |
| + | [[File:izzard1.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Hydrogramme sans dimension de Izzard ; <u>Source</u> : Deutsch ''et al'' (1989)].</center>'']] | ||
| + | * L'existence de relations empiriques entre les deux grandeurs de base (<math>Q_{eq}</math> et <math>t_{eq}</math>), le stockage superficiel instantané (<math>D_e</math>), l'intensité moyenne de pluie nette (<math>i_n</math>) et les données caractérisant le bassin versant : | ||
| − | |||
| − | |||
| − | |||
| + | <center><math>t_{eq}=2.\frac{D_e}{60}.Q_{eq}</math></center> | ||
| − | + | <center><math>D_e=4{,}39.10^{-3}.(2{,}76.10^{-5}.i_n+c).L^{3/4}.i_n^{1/3}.I^{-1/3}</math></center> | |
| − | <center> | + | <center><math>Q_{eq}=2{,}778.10^{-7}.i_n.L</math></center> |
| − | + | Avec : | |
| − | + | * <math>c</math> : paramètre représentant le coefficient de rugosité et fonction de la nature du revêtement ; | |
| − | + | * <math>D_e</math> : volume stocké par unité de largeur (m<sup>3</sup>/m) ; | |
| − | + | * <math>I</math> : pente de la surface (m/m) ; | |
| − | + | * <math>i_n</math> : intensité de pluie nette constante (mm/h) ; | |
| − | + | * <math>L</math> : longueur du ruissellement (m) ; | |
| − | + | * <math>Q_{eq}</math> : débit (m<sup>3</sup>/s/m) ; | |
| − | + | * <math>t{eq}</math> : temps (mn). | |
| − | + | ||
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | * | + | |
| − | + | ||
| − | * I : pente de la surface (m /m) | + | |
| − | + | ||
| − | * | + | |
| − | + | ||
| − | * L : longueur du ruissellement (m) | + | |
| − | + | ||
| − | * | + | |
| − | + | ||
| − | * | + | |
== Choix des paramètres == | == Choix des paramètres == | ||
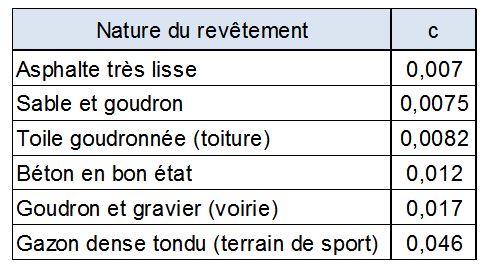
| − | Le tableau | + | Le tableau de la ''figure 2'' donne quelques indications pour le choix de <math>c</math> |
| − | de c | + | |
| − | |||
| − | + | [[File:Izzard3.JPG|600px|center|thumb|<center>''<u>Figure 2</u> : Valeurs à attribuer au coefficient de rugosité <math>c</math> de la formule de Izzard en fonction de la nature de la surface d'écoulement ; <u>Source</u> : Deutsch ''et al.'', (1989)''</center>]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Valeurs à attribuer au coefficient de rugosité c de la | + | |
| − | formule de Izzard en fonction de la nature de la surface d'écoulement | + | |
| − | + | ||
| − | </center> | + | |
== Utilisation pratique == | == Utilisation pratique == | ||
| − | Le modèle d’Izzard peut fournir un [[Hydrogramme (HU)|hydrogramme]] complet | + | Le modèle d’Izzard peut fournir un [[Hydrogramme (HU)|hydrogramme]] complet à l'exutoire correspondant à un [[Hyétogramme (HU)|hyétogramme]] quelconque. Il suffit de décomposer le hyétogramme en pas de temps d'intensité constante et d'appliquer la méthode à chacune des averses élémentaires d'intensité constante ainsi obtenues. La réponse à l'entrée complète sera obtenue en sommant les réponses à chacune des entrées élémentaires (principe de superposition des solutions). Cette technique nécessite cependant d'associer à l'hydrogramme sans dimension qui ne représente que la montée en débit, une fonction permettant de représenter la décrue correspondant à chaque pluie élémentaire. Cette fonction se calcule de la façon suivante : à la fin de chaque période de pluie élémentaire, il reste sur le sol un stock <math>D_0</math>, due à cette pluie élémentaire, égal au volume précipité moins le volume écoulé. Durant la période de décrue de l'hydrogramme élémentaire, il existe une relation empirique entre le débit à l'instant <math>t_r</math> (temps écoulé depuis la fin de la pluie élémentaire d'intensité constante) et le débit <math>Q_d</math> à la fin de cet instant : |
| − | à l'exutoire correspondant à un [[Hyétogramme (HU)|hyétogramme]] | + | |
| − | quelconque. Il suffit de décomposer le hyétogramme en pas de temps d'intensité | + | |
| − | constante et d'appliquer la méthode à chacune des averses élémentaires | + | |
| − | d'intensité constante ainsi obtenues. La réponse à l'entrée complète sera | + | |
| − | obtenue en sommant les réponses à chacune des entrées élémentaires (principe de | + | |
| − | superposition des solutions). Cette technique nécessite cependant d'associer à | + | |
| − | l'hydrogramme sans dimension qui ne représente que la montée en débit, une | + | |
| − | fonction permettant de représenter la décrue correspondant à chaque pluie | + | |
| − | élémentaire. Cette fonction se calcule de la façon | + | |
| − | chaque période de pluie élémentaire, il reste sur le sol un stock | + | |
| − | due à cette pluie élémentaire, égal au volume précipité moins le volume écoulé. | + | |
| − | Durant la période de décrue de l'hydrogramme élémentaire, il existe une | + | |
| − | relation empirique entre le débit à l'instant | + | |
| − | depuis la fin de la pluie élémentaire d'intensité constante) et le débit | + | |
| − | à la fin de cet | + | |
| + | <center><math>t_r=\frac{0{,}5.D_0.(r^{-2/3}-1)}{60.Q_{eq}}</math></center> | ||
| − | |||
| + | Avec : | ||
| − | + | <center><math>r=\frac{Q_d}{Q_{eq}}</math></center> | |
| + | == Intérêt et limites == | ||
| − | + | Élaboré à l'origine pour représenter le [[Ruissellement urbain (HU)|ruissellement]] sur des aéroports, ce modèle s'applique bien à l'étude du ruissellement sur des bassins versants ayant une largeur sensiblement constante comme les routes ou les autoroutes. Il a d'ailleurs été à l'origine de la méthode des temps d'équilibre utilisée en France pour l'assainissement des autoroutes. D'une façon plus générale, il convient bien à des écoulements sur des éléments plans homogènes, de pente relativement faible (moins de 4%). En revanche, son application à des bassins versants urbains de surface supérieure à quelques hectares, fortement équipés en ouvrages souterrains d'assainissement, est à proscrire. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <u>Bibliographie</u> : | |
| − | + | * Izzard, C.G. (1946) : ''Hydraulics of runoff from developed surfaces'' ; ''proceedings of the 26th annual meeting'' ; ''highway Research Board'', Vol. 26 ; pp. 129-146 ; 1946 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <u>Pour en savoir plus</u> | + | <u>Pour en savoir plus</u> : |
| − | 1989 | + | * Deutsch ''et al.'' (1989) : Groupe de Travail du STU animé par Deutsch J.C. ; Mémento sur l'évacuation des eaux pluviales ; La documentation française ; Paris ; 349 p. ; 1989. |
| − | sur l'évacuation des eaux | + | |
| − | + | ||
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
| + | [[Catégorie:Modélisation_de_la_transformation_pluie-débit_(HU)]] | ||
Version actuelle en date du 23 mai 2024 à 10:35
Traduction anglaise : Izzard's model
Dernière mise à jour : 23/05/2024
Modèle empirique proposé par Izzard (1946) pour représenter la transformation pluie nette - débit à l'exutoire d'un bassin versant.
Sommaire |
[modifier] Hypothèses et formulation
Le modèle d'Izzard consiste à construire un hydrogramme unitaire synthétique en s'appuyant sur les éléments suivants :
- L'indépendance entre la fonction de transfert et la pluie à l'origine du ruissellement (linéarité du phénomène). Cette hypothèse permet de déduire l'existence d'un hydrogramme sans dimension représentant la réponse du bassin versant à une pluie unitaire constante. Cet hydrogramme sans dimension utilise des variables normées pour les débits et les temps. Les normes sont respectivement le débit à l'équilibre : $ Q_{eq} $ et le temps d'équilibre : $ t_{eq} $ (figure 1).
Le temps d'équilibre est défini arbitrairement comme le temps au bout duquel le débit observé devient égal à 97% du débit d'équilibre :
- L'existence de relations empiriques entre les deux grandeurs de base ($ Q_{eq} $ et $ t_{eq} $), le stockage superficiel instantané ($ D_e $), l'intensité moyenne de pluie nette ($ i_n $) et les données caractérisant le bassin versant :
Avec :
- $ c $ : paramètre représentant le coefficient de rugosité et fonction de la nature du revêtement ;
- $ D_e $ : volume stocké par unité de largeur (m3/m) ;
- $ I $ : pente de la surface (m/m) ;
- $ i_n $ : intensité de pluie nette constante (mm/h) ;
- $ L $ : longueur du ruissellement (m) ;
- $ Q_{eq} $ : débit (m3/s/m) ;
- $ t{eq} $ : temps (mn).
[modifier] Choix des paramètres
Le tableau de la figure 2 donne quelques indications pour le choix de $ c $
[modifier] Utilisation pratique
Le modèle d’Izzard peut fournir un hydrogramme complet à l'exutoire correspondant à un hyétogramme quelconque. Il suffit de décomposer le hyétogramme en pas de temps d'intensité constante et d'appliquer la méthode à chacune des averses élémentaires d'intensité constante ainsi obtenues. La réponse à l'entrée complète sera obtenue en sommant les réponses à chacune des entrées élémentaires (principe de superposition des solutions). Cette technique nécessite cependant d'associer à l'hydrogramme sans dimension qui ne représente que la montée en débit, une fonction permettant de représenter la décrue correspondant à chaque pluie élémentaire. Cette fonction se calcule de la façon suivante : à la fin de chaque période de pluie élémentaire, il reste sur le sol un stock $ D_0 $, due à cette pluie élémentaire, égal au volume précipité moins le volume écoulé. Durant la période de décrue de l'hydrogramme élémentaire, il existe une relation empirique entre le débit à l'instant $ t_r $ (temps écoulé depuis la fin de la pluie élémentaire d'intensité constante) et le débit $ Q_d $ à la fin de cet instant :
Avec :
[modifier] Intérêt et limites
Élaboré à l'origine pour représenter le ruissellement sur des aéroports, ce modèle s'applique bien à l'étude du ruissellement sur des bassins versants ayant une largeur sensiblement constante comme les routes ou les autoroutes. Il a d'ailleurs été à l'origine de la méthode des temps d'équilibre utilisée en France pour l'assainissement des autoroutes. D'une façon plus générale, il convient bien à des écoulements sur des éléments plans homogènes, de pente relativement faible (moins de 4%). En revanche, son application à des bassins versants urbains de surface supérieure à quelques hectares, fortement équipés en ouvrages souterrains d'assainissement, est à proscrire.
Bibliographie :
- Izzard, C.G. (1946) : Hydraulics of runoff from developed surfaces ; proceedings of the 26th annual meeting ; highway Research Board, Vol. 26 ; pp. 129-146 ; 1946
Pour en savoir plus :
- Deutsch et al. (1989) : Groupe de Travail du STU animé par Deutsch J.C. ; Mémento sur l'évacuation des eaux pluviales ; La documentation française ; Paris ; 349 p. ; 1989.
 S'abonner à un flux RSS
S'abonner à un flux RSS