Isohyète (HU) : Différence entre versions
m (1 version) |
|||
| (7 révisions intermédiaires par 2 utilisateurs sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Isohyet, Isohyetal line'' | ''<u>Traduction anglaise</u> : Isohyet, Isohyetal line'' | ||
| − | + | <u>Dernière mise à jour</u> : 03/03/2025 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
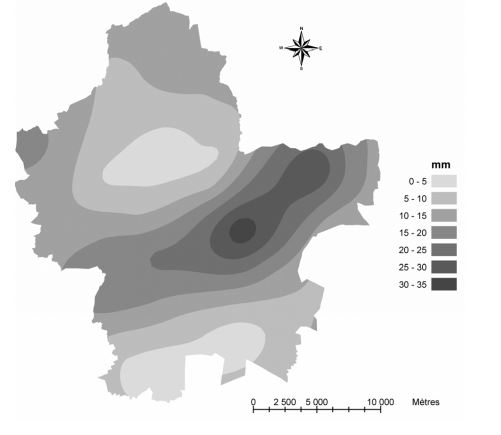
| − | [[Catégorie: | + | Courbe d'égale hauteur d'eau précipitée pendant un [[Evénement pluvieux (HU)|événement pluvieux]] ou pendant une période donnée (''figure 1''). |
| + | |||
| + | |||
| + | [[File:isohyete.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Exemple de courbes isohyète ; <u>Source</u> : [https://www.aquaportail.com/definition-2561-isohyete.html aquaportail].''</center>]] | ||
| + | |||
| + | ==Intérêt des courbes isohyètes== | ||
| + | |||
| + | Ces courbes permettent une représentation spatiale de la répartition de la pluie. Il s'agit donc d'un modèle simple de [[Répartition spatio-temporelle des précipitations (HU)|répartition spatiale]] qui permet, par exemple, de passer d'un ensemble de mesures réalisées sur un nombre limité de postes à une lame d'eau moyenne sur différentes surfaces et en particulier sur un bassin versant. | ||
| + | |||
| + | ==Mode de construction des courbes isohyètes== | ||
| + | |||
| + | Dans le cas où les données de départ sont issues de mesures effectuées au sol sur un réseau de pluviomètres, le tracé des isohyètes repose sur l'utilisation de modèles génériques d'interpolation spatiale éventuellement fondés sur des méthodes de [[Géostatistique (HU)|géostatistique]]. L'un des modèles classiques le plus ancien est celui des [[Thyssen (polygones de) (HU)|polygones de Thyssen]] qui revient en fait à affecter à tout point du territoire l'intensité ou la hauteur d'eau mesurée sur le poste pluviométrique le plus proche. Depuis, de nombreuses méthodes d'interpolation (utilisant par exemple les [[Spline (fonction) (HU)|fonctions splines]]) (''figure 2'') ou d'approximation ont été proposées. On en trouvera une synthèse critique par exemple dans Renard & Comby (2006). | ||
| + | |||
| + | |||
| + | [[File:krigeage.JPG|600px|center|thumb|<center>''<u>Figure 2</u> : Représentation d'un champ de pluie par une fonction spline ; <u>Source</u> : Renard et Comby (2006).''</center>]] | ||
| + | |||
| + | L'utilisation combinée de mesures issues d'un [[Radar météorologique (HU)|radar météorologique]] et de mesures au sol obtenues par des [[Pluviomètre (HU)|pluviomètres]] facilite la construction des courbes isohyètes (comme celle des autres modèles de répartition spatiale des pluies). | ||
| + | |||
| + | ==Cas des événements pluvieux intenses== | ||
| + | |||
| + | Le tracé des courbes isohyètes, même à partir des données issues d'un réseau de mesure comportant plusieurs dizaines de [[Pluviomètre (HU)|pluviomètres]] est peu fiable pour les événements courts et intenses critiques sur les petits bassins versants. Les différentes méthodes utilisables supposent que le phénomène soit continu entre les postes, voire, pour la plupart, que les variations de l'intensité soient linéaires. Ces hypothèses sur la répartition spatiale des précipitations sont généralement assez mal vérifiées (par l’observation [[Radar météorologique (HU)|radar météorologique]] en particulier), notamment pour des durées courtes (inférieure à 24 heures). Les courbes isohyètes doivent donc être considérées avec d'autant plus de prudence que la durée pour laquelle elles ont été établies est courte. | ||
| + | |||
| + | <u>Bibliographie</u> : | ||
| + | * Renard, F., Comby, J. (2006) : Évaluation de techniques d’interpolation spatiale de la pluie en milieu urbain pour une meilleure gestion d’événements extrêmes : le cas du Grand Lyon ; [http://www.shf-lhb.org/ LA HOUILLE BLANCHE/N° 6-2006.] | ||
| + | |||
| + | <u>Voir</u> : [[Répartition spatio-temporelle des précipitations (HU)|Répartition spatio-temporelle des précipitations]]. | ||
| + | |||
| + | [[Catégorie:Dictionnaire_DEHUA]] | ||
| + | [[Catégorie:Modélisation_de_la_pluie_(HU)]] | ||
Version actuelle en date du 3 mars 2025 à 10:40
Traduction anglaise : Isohyet, Isohyetal line
Dernière mise à jour : 03/03/2025
Courbe d'égale hauteur d'eau précipitée pendant un événement pluvieux ou pendant une période donnée (figure 1).
[modifier] Intérêt des courbes isohyètes
Ces courbes permettent une représentation spatiale de la répartition de la pluie. Il s'agit donc d'un modèle simple de répartition spatiale qui permet, par exemple, de passer d'un ensemble de mesures réalisées sur un nombre limité de postes à une lame d'eau moyenne sur différentes surfaces et en particulier sur un bassin versant.
[modifier] Mode de construction des courbes isohyètes
Dans le cas où les données de départ sont issues de mesures effectuées au sol sur un réseau de pluviomètres, le tracé des isohyètes repose sur l'utilisation de modèles génériques d'interpolation spatiale éventuellement fondés sur des méthodes de géostatistique. L'un des modèles classiques le plus ancien est celui des polygones de Thyssen qui revient en fait à affecter à tout point du territoire l'intensité ou la hauteur d'eau mesurée sur le poste pluviométrique le plus proche. Depuis, de nombreuses méthodes d'interpolation (utilisant par exemple les fonctions splines) (figure 2) ou d'approximation ont été proposées. On en trouvera une synthèse critique par exemple dans Renard & Comby (2006).
L'utilisation combinée de mesures issues d'un radar météorologique et de mesures au sol obtenues par des pluviomètres facilite la construction des courbes isohyètes (comme celle des autres modèles de répartition spatiale des pluies).
[modifier] Cas des événements pluvieux intenses
Le tracé des courbes isohyètes, même à partir des données issues d'un réseau de mesure comportant plusieurs dizaines de pluviomètres est peu fiable pour les événements courts et intenses critiques sur les petits bassins versants. Les différentes méthodes utilisables supposent que le phénomène soit continu entre les postes, voire, pour la plupart, que les variations de l'intensité soient linéaires. Ces hypothèses sur la répartition spatiale des précipitations sont généralement assez mal vérifiées (par l’observation radar météorologique en particulier), notamment pour des durées courtes (inférieure à 24 heures). Les courbes isohyètes doivent donc être considérées avec d'autant plus de prudence que la durée pour laquelle elles ont été établies est courte.
Bibliographie :
- Renard, F., Comby, J. (2006) : Évaluation de techniques d’interpolation spatiale de la pluie en milieu urbain pour une meilleure gestion d’événements extrêmes : le cas du Grand Lyon ; LA HOUILLE BLANCHE/N° 6-2006.
 S'abonner à un flux RSS
S'abonner à un flux RSS