Caractéristique (courbe) (HU) : Différence entre versions
| (9 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
| + | [[File:logo_eurydice.jpg|80px]][[File:Logo OFB_soutien financier.png|120px]] | ||
| + | |||
''<u>Traduction anglaise</u> : Characteristics'' | ''<u>Traduction anglaise</u> : Characteristics'' | ||
| − | <u>Dernière mise à jour</u> : | + | <u>Dernière mise à jour</u> : 28/06/2025 |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | En hydraulique l'expression "courbes caractéristiques" est utilisée dans deux sens différents. | |
| + | * Pour une pompe, il s'agit des courbes représentant les relations entre le débit <math>Q</math>, la hauteur totale <math>H_t</math>, la puissance absorbée <math>P</math> et le rendement <math>η</math> caractérisant la pompe dans des conditions données de fonctionnement ; ce sens est développé dans l'article [[Caractéristique (d'une pompe) (HU)]] ; | ||
| + | * Pour une équation aux dérivées partielles hyperboliques (ou pour un système d'équations aux dérivées partielles), dont font partie les équations de propagation d'ondes, les courbes caractéristiques (ou les surfaces caractéristiques si le système a plus de deux dimensions) sont les courbes (ou les surfaces) sur lesquelles se propagent les perturbations ; c'est ce deuxième sens qui est développé dans cet article. | ||
== Interprétation intuitive en hydraulique== | == Interprétation intuitive en hydraulique== | ||
| − | En hydraulique, il est possible d'imager ces courbes dans un cas simple : considérons un plan d'eau parfaitement tranquille. A l'instant <math>t = 0</math>, on jette un caillou en un point particulier de ce plan d'eau. Ce caillou provoque l'apparition d'ondes qui se déplacent à partir du point d'impact. Si l'on trace une droite passant par le point d'impact et que l'on représente par la variable <math>x</math> la position d'un point sur cet axe, il est possible de représenter le déplacement de la première onde dans un repère <math>x, t</math> (<math>t</math> représentant le temps). | + | En hydraulique, il est possible d'imager ces courbes dans un cas simple : considérons un plan d'eau parfaitement tranquille. A l'instant <math>t = 0</math>, on jette un caillou en un point particulier de ce plan d'eau. Ce caillou provoque l'apparition d'ondes qui se déplacent à partir du point d'impact. Si l'on trace une droite passant par le point d'impact et que l'on représente par la variable <math>x</math> la position d'un point sur cet axe, il est possible de représenter le déplacement de la première onde dans un repère <math>x, t</math> (<math>t</math> représentant le temps) (''figure 1''). |
| − | [[File:caractéristiques1.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Représentation schématique de la propagation d'une perturbation dans l'espace abscisse-temps.''</center>]] | + | |
| + | [[File:caractéristiques1.JPG|600px|center|thumb|<center>''<u>Figure 1</u> : Représentation schématique de la propagation d'une perturbation dans l'espace abscisse-temps pour un fluide immobile.''</center>]] | ||
Les deux courbes obtenues sont les courbes caractéristiques de l'équation régissant le phénomène. Elles séparent le domaine en deux sous-domaines aux propriétés très différentes : | Les deux courbes obtenues sont les courbes caractéristiques de l'équation régissant le phénomène. Elles séparent le domaine en deux sous-domaines aux propriétés très différentes : | ||
| − | * la partie non hachurée n'est pas encore perturbée par le fait que l'on a jeté un caillou. En fait, l'information | + | * la partie non hachurée n'est pas encore perturbée par le fait que l'on a jeté un caillou. En fait, l'information "''on a jeté un caillou''" n'est pas encore arrivée jusqu'en ces points ; |
* la partie hachurée, pour sa part a reçu l'information et son état dépend du fait que l'on a jeté un caillou. | * la partie hachurée, pour sa part a reçu l'information et son état dépend du fait que l'on a jeté un caillou. | ||
| Ligne 23 : | Ligne 24 : | ||
Ces courbes jouent un rôle important dans deux domaines : | Ces courbes jouent un rôle important dans deux domaines : | ||
| − | * la séparation des régimes d’écoulement (séparation entre régime torrentiel et régime fluvial) ; | + | * la séparation des [[Régime d’écoulement (HU)|régimes d’écoulement]] (séparation entre [[Ecoulement torrentiel (HU)|régime torrentiel]] et [[Ecoulement fluvial (HU)|régime fluvial]]) ; |
* l’analyse de la stabilité des schémas numériques de résolution des équations. | * l’analyse de la stabilité des schémas numériques de résolution des équations. | ||
| − | Considérons | + | ===Stabilité des schémas numériques=== |
| + | |||
| + | Considérons un point quelconque <math>A</math>, situé à l'abscisse <math>x</math> et au temps <math>t</math> (''figure 2''). Ce point est situé à l'intersection de deux courbes caractéristiques, l'une provenant de la droite et l'autre de la gauche (des <math>x</math> négatifs et des <math>x</math> positifs). Au temps <math>t - Δt</math>, ces deux courbes passaient respectivement par les positions <math>x - Δx</math> et <math>x + Δx</math>. Ceci signifie que l'état du milieu au point <math>x</math> dépend de l'état du milieu au temps <math>t - Δt</math> entre les points <math>x - Δx</math> et <math>x + Δx</math>, mais qu'il est indépendant de l'état du milieu au même instant et à l'extérieur de ce domaine, l'information n'ayant pas eu le temps d'arriver jusqu'à l'abscisse <math>x</math>. | ||
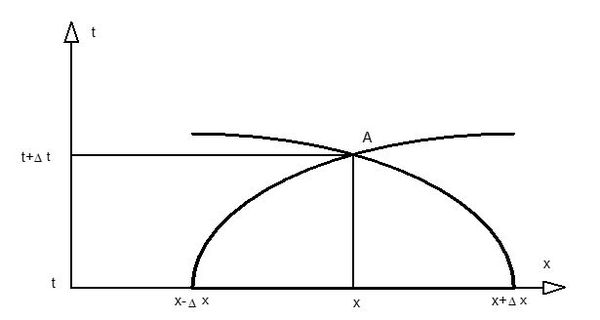
[[File:caractéristique2.JPG|600px|center|thumb|<center>''<u>Figure 2</u> : Domaine d'influence du point <math>A</math>.''</center>]] | [[File:caractéristique2.JPG|600px|center|thumb|<center>''<u>Figure 2</u> : Domaine d'influence du point <math>A</math>.''</center>]] | ||
| + | Ceci montre qu’il existe une relation entre la [[Célérité (HU)|célérité]] de l’onde, <math>c</math> et les pas de temps, <math>Δt</math> et d’espace, <math>Δx</math>, relation qui doit être vérifiée pour assurer la [[Stabilité (HU)|stabilité]] du schéma de résolution. Dans le cas d'un schéma explicite, cette relation se met sous la forme : | ||
| − | + | <center><math>\frac{Δx}{Δt}\ ≥\ c</math></center> | |
| + | Dans le cas des équations de [[Barré de Saint Venant (équations de) (HU)|Barré de Saint Venant]], les ondes se propagent dans un milieu qui est lui-même en mouvement, l'eau s'écoulant de l'amont vers l'aval à la vitesse <math>V</math>. Le déplacement des ondes dans un repère fixe <math>x, t</math> s'effectue donc à la vitesse <math>V + c</math> pour l'onde "descendante" (allant de l'amont vers l'aval) et à la vitesse <math>V - c</math> pour l'onde "montante". | ||
| − | + | On retrouve ainsi simplement, dans le cas d'un schéma explicite, la [[Courant-Friedrich-Levy / CFL (condition de) (HU)|condition de Courant-Friedrisch-Levy]] : | |
| − | + | <center><math>\frac{Δx}{Δt}\ ≥\ |V\ ±\ c|</math></center> | |
| − | |||
| + | Il est important de préciser que l'établissement de cette condition nécessite que la dérivée seconde de la relation entre la [[Section mouillée (HU)|section mouillée]] et la hauteur soit nulle, c'est-à-dire, pratiquement, que la section soit rectangulaire. | ||
| + | En eau peu profonde, la célérité <math>c</math> dépend uniquement de la hauteur d'eau et peut s'exprimer sous la forme : | ||
| − | |||
| + | <center><math>c = \sqrt{g.h} </math></center> | ||
| − | + | avec : | |
| + | * <math>c</math> : célérité (m/s) ; | ||
| + | * <math>g</math> : accélération de la pesanteur (m/s<sup>2</sup>) ; | ||
| + | * <math>h</math> : hauteur d'eau (m). | ||
| + | Le rapport de la vitesse sur la célérité de l'onde est égal au nombre de Froude : | ||
| + | |||
| + | |||
| + | <center><math>Fr = \frac{V}{\sqrt{g.h}} </math></center> | ||
| + | |||
| + | ===Écoulement fluvial, critique et torrentiel=== | ||
| + | |||
| + | Selon la valeur relative de la vitesse et de la célérité, trois cas sont possibles : | ||
| + | * si l'onde se déplace plus vite que l'eau (<math>V < c</math>, soit <math>Fr < 1</math>), l'une des deux ondes va vers l'amont et l'autre vers l'aval ; ce cas correspond au [[Ecoulement fluvial (HU)|régime fluvial]] ; | ||
| + | * si l'onde se déplace moins vite que l'eau (<math>c < V</math>, soit <math>Fr > 1</math>), les deux ondes vont de l'amont vers l'aval ; ce cas correspond au [[Ecoulement torrentiel (HU)|régime torrentiel]] ; | ||
| + | * si l'onde se déplace à la même vitesse que l'eau (soit <math>Fr = 1</math>, l'une des deux ondes est stationnaire ; ce cas correspond au [[Ecoulement critique (HU)|régime critique]]. | ||
| + | |||
<u>Voir</u> : [[Ecoulement (HU)|Ecoulement]]. | <u>Voir</u> : [[Ecoulement (HU)|Ecoulement]]. | ||
| − | == Utilisation | + | Cette analyse indique également les conditions aux limites nécessaires pour "fermer" le système : |
| + | * 2 à l'amont pour un régime torrentiel (sur un plan calculatoire on peut simplifier les équations et une seule condition est généralement suffisante) ; | ||
| + | * 1 à l'amont et 1 à l'aval en régime fluvial ; | ||
| + | * 1 à l'aval en régime critique. | ||
| + | |||
| + | <u>Voir</u> : [[Barré de Saint Venant (équations de) (HU)|Barré de Saint Venant (équations de)]]. | ||
| + | |||
| + | ==Utilisation des courbes caractéristiques pour la résolution des équations== | ||
| + | |||
| + | De façon plus précise si les équations représentent un phénomène de propagation d'ondes se déplaçant à la célérité <math>c</math> dans un repère fixe (eulérien), les caractéristiques constituent des courbes ou des surfaces particulières (équations à une ou plusieurs dimensions d'espace), le long desquelles, pour un observateur se déplaçant à la célérité des ondes, les équations aux dérivées partielles apparaissent comme des équations différentielles totales qui peuvent, dans les cas simples (équations linéaires), être résolues analytiquement. Cette méthode de résolution est due au mathématicien Gaspard Monge (1748-1818) qui l'appliqua, en 1809, à l'étude de l'équation des cordes vibrantes. | ||
| − | En hydraulique, cette méthode a parfois été utilisée pour résoudre le système d'équations de [[Barré de Saint Venant (équations de) (HU)|Barré de Saint Venant]]. Elle est maintenant tombée en désuétude. | + | En hydraulique, cette méthode a parfois été utilisée pour résoudre le système d'équations de [[Barré de Saint Venant (équations de) (HU)|Barré de Saint Venant]]. Elle est maintenant tombée en désuétude. En effet elle est peu pratique à manipuler et les ordinateurs permettent de résoudre plus facilement et plus rapidement ces équations par la [[Différences finies (méthode des) (HU)|méthode des différences finies]] ou par la [[Eléments finis (méthode des) (HU)|méthode des éléments finis]]. |
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
Version actuelle en date du 28 juin 2025 à 09:43
Traduction anglaise : Characteristics
Dernière mise à jour : 28/06/2025
En hydraulique l'expression "courbes caractéristiques" est utilisée dans deux sens différents.
- Pour une pompe, il s'agit des courbes représentant les relations entre le débit $ Q $, la hauteur totale $ H_t $, la puissance absorbée $ P $ et le rendement $ η $ caractérisant la pompe dans des conditions données de fonctionnement ; ce sens est développé dans l'article Caractéristique (d'une pompe) (HU) ;
- Pour une équation aux dérivées partielles hyperboliques (ou pour un système d'équations aux dérivées partielles), dont font partie les équations de propagation d'ondes, les courbes caractéristiques (ou les surfaces caractéristiques si le système a plus de deux dimensions) sont les courbes (ou les surfaces) sur lesquelles se propagent les perturbations ; c'est ce deuxième sens qui est développé dans cet article.
Sommaire |
[modifier] Interprétation intuitive en hydraulique
En hydraulique, il est possible d'imager ces courbes dans un cas simple : considérons un plan d'eau parfaitement tranquille. A l'instant $ t = 0 $, on jette un caillou en un point particulier de ce plan d'eau. Ce caillou provoque l'apparition d'ondes qui se déplacent à partir du point d'impact. Si l'on trace une droite passant par le point d'impact et que l'on représente par la variable $ x $ la position d'un point sur cet axe, il est possible de représenter le déplacement de la première onde dans un repère $ x, t $ ($ t $ représentant le temps) (figure 1).
Les deux courbes obtenues sont les courbes caractéristiques de l'équation régissant le phénomène. Elles séparent le domaine en deux sous-domaines aux propriétés très différentes :
- la partie non hachurée n'est pas encore perturbée par le fait que l'on a jeté un caillou. En fait, l'information "on a jeté un caillou" n'est pas encore arrivée jusqu'en ces points ;
- la partie hachurée, pour sa part a reçu l'information et son état dépend du fait que l'on a jeté un caillou.
[modifier] Importance des courbes caractéristiques en hydraulique
Ces courbes jouent un rôle important dans deux domaines :
- la séparation des régimes d’écoulement (séparation entre régime torrentiel et régime fluvial) ;
- l’analyse de la stabilité des schémas numériques de résolution des équations.
[modifier] Stabilité des schémas numériques
Considérons un point quelconque $ A $, situé à l'abscisse $ x $ et au temps $ t $ (figure 2). Ce point est situé à l'intersection de deux courbes caractéristiques, l'une provenant de la droite et l'autre de la gauche (des $ x $ négatifs et des $ x $ positifs). Au temps $ t - Δt $, ces deux courbes passaient respectivement par les positions $ x - Δx $ et $ x + Δx $. Ceci signifie que l'état du milieu au point $ x $ dépend de l'état du milieu au temps $ t - Δt $ entre les points $ x - Δx $ et $ x + Δx $, mais qu'il est indépendant de l'état du milieu au même instant et à l'extérieur de ce domaine, l'information n'ayant pas eu le temps d'arriver jusqu'à l'abscisse $ x $.
Ceci montre qu’il existe une relation entre la célérité de l’onde, $ c $ et les pas de temps, $ Δt $ et d’espace, $ Δx $, relation qui doit être vérifiée pour assurer la stabilité du schéma de résolution. Dans le cas d'un schéma explicite, cette relation se met sous la forme :
Dans le cas des équations de Barré de Saint Venant, les ondes se propagent dans un milieu qui est lui-même en mouvement, l'eau s'écoulant de l'amont vers l'aval à la vitesse $ V $. Le déplacement des ondes dans un repère fixe $ x, t $ s'effectue donc à la vitesse $ V + c $ pour l'onde "descendante" (allant de l'amont vers l'aval) et à la vitesse $ V - c $ pour l'onde "montante".
On retrouve ainsi simplement, dans le cas d'un schéma explicite, la condition de Courant-Friedrisch-Levy :
Il est important de préciser que l'établissement de cette condition nécessite que la dérivée seconde de la relation entre la section mouillée et la hauteur soit nulle, c'est-à-dire, pratiquement, que la section soit rectangulaire.
En eau peu profonde, la célérité $ c $ dépend uniquement de la hauteur d'eau et peut s'exprimer sous la forme :
avec :
- $ c $ : célérité (m/s) ;
- $ g $ : accélération de la pesanteur (m/s2) ;
- $ h $ : hauteur d'eau (m).
Le rapport de la vitesse sur la célérité de l'onde est égal au nombre de Froude :
[modifier] Écoulement fluvial, critique et torrentiel
Selon la valeur relative de la vitesse et de la célérité, trois cas sont possibles :
- si l'onde se déplace plus vite que l'eau ($ V < c $, soit $ Fr < 1 $), l'une des deux ondes va vers l'amont et l'autre vers l'aval ; ce cas correspond au régime fluvial ;
- si l'onde se déplace moins vite que l'eau ($ c < V $, soit $ Fr > 1 $), les deux ondes vont de l'amont vers l'aval ; ce cas correspond au régime torrentiel ;
- si l'onde se déplace à la même vitesse que l'eau (soit $ Fr = 1 $, l'une des deux ondes est stationnaire ; ce cas correspond au régime critique.
Voir : Ecoulement.
Cette analyse indique également les conditions aux limites nécessaires pour "fermer" le système :
- 2 à l'amont pour un régime torrentiel (sur un plan calculatoire on peut simplifier les équations et une seule condition est généralement suffisante) ;
- 1 à l'amont et 1 à l'aval en régime fluvial ;
- 1 à l'aval en régime critique.
Voir : Barré de Saint Venant (équations de).
[modifier] Utilisation des courbes caractéristiques pour la résolution des équations
De façon plus précise si les équations représentent un phénomène de propagation d'ondes se déplaçant à la célérité $ c $ dans un repère fixe (eulérien), les caractéristiques constituent des courbes ou des surfaces particulières (équations à une ou plusieurs dimensions d'espace), le long desquelles, pour un observateur se déplaçant à la célérité des ondes, les équations aux dérivées partielles apparaissent comme des équations différentielles totales qui peuvent, dans les cas simples (équations linéaires), être résolues analytiquement. Cette méthode de résolution est due au mathématicien Gaspard Monge (1748-1818) qui l'appliqua, en 1809, à l'étude de l'équation des cordes vibrantes.
En hydraulique, cette méthode a parfois été utilisée pour résoudre le système d'équations de Barré de Saint Venant. Elle est maintenant tombée en désuétude. En effet elle est peu pratique à manipuler et les ordinateurs permettent de résoudre plus facilement et plus rapidement ces équations par la méthode des différences finies ou par la méthode des éléments finis.
 S'abonner à un flux RSS
S'abonner à un flux RSS