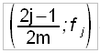S'abonner à un flux RSS
D.09 - Diagramme de fiabilité : Différence entre versions
(→Variante : événements binaires et dépassements de seuil) |
|||
| (2 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
== Principe == | == Principe == | ||
| − | Le diagramme de fiabilité permet la même évaluation de la fiabilité d'un système de prévision que le diagramme de Talagrand (fiche | + | Le diagramme de fiabilité permet la même évaluation de la fiabilité d'un système de prévision que le diagramme de Talagrand ([[D.08_-_Diagramme_de_Talagrand_(diagramme_de_rang)|fiche D.08]]). Il permet la comparaison de la probabilité prévue d'un aléa (axe des abscisses) et de sa fréquence d'observation (axe des ordonnées). Un système de prévision fiable doit fournir des probabilités prévues proches des fréquences d'observation correspondantes : son diagramme de fiabilité sera donc proche de la bissectrice. |
La suite de cette fiche présente deux manières pour construire le diagramme. | La suite de cette fiche présente deux manières pour construire le diagramme. | ||
| Ligne 18 : | Ligne 18 : | ||
Pour chaque prévision i, le quantile de prévision q<sub>y</sub> (X<sub>i</sub>) est défini par le fait que la probabilité de non dépassement de cette valeur est égale à y : [[File:Inc289.bmp|140px]]. | Pour chaque prévision i, le quantile de prévision q<sub>y</sub> (X<sub>i</sub>) est défini par le fait que la probabilité de non dépassement de cette valeur est égale à y : [[File:Inc289.bmp|140px]]. | ||
| − | Si l'estimation Q<sub>y</sub>(X) du quantile est fiable alors la fréquence d'observation du non dépassement de cette valeurdoit être proche de y et donc le point doit être proche de la bissectrice | + | Si l'estimation Q<sub>y</sub>(X) du quantile est fiable alors la fréquence d'observation du non dépassement de cette valeurdoit être proche de y et donc le point doit être proche de la bissectrice<ref>Autrement dit, cela revient à compter sur l'ensemble des prévisions, combien d'observations ne dépassent pas le quantile de prévision Q<sub>y</sub>(X) – par exemple le quantile ''q<sub>10 %</sub>'' –, et à vérifier que l'on observe ce non dépassement à une fréquence proche de y (ici 10 %).</ref>. |
Cette procédure est reproduite pour différents points (différents quantiles de prévision Q<sub>y</sub>(X)) pour obtenir le diagramme de fiabilité en reliant ces points (Fig.1, au verso). | Cette procédure est reproduite pour différents points (différents quantiles de prévision Q<sub>y</sub>(X)) pour obtenir le diagramme de fiabilité en reliant ces points (Fig.1, au verso). | ||
| Ligne 24 : | Ligne 24 : | ||
== Variante : événements binaires et dépassements de seuil == | == Variante : événements binaires et dépassements de seuil == | ||
| − | Dans le cas où l'événement à prévoir ne peut prendre que deux valeurs A et B, comme un dépassement de seuil | + | Dans le cas où l'événement à prévoir ne peut prendre que deux valeurs A et B, comme un dépassement de seuil<ref>Dans ce cas, la valeur A correspond au non dépassement de seuil et la valeur B au dépassement.</ref>, le diagramme de fiabilité peut être construit ainsi : |
* a. Les n prévisions sont séparées en m groupes tels que chaque sous-groupe j contient les prévisions dont les probabilités de A (du non dépassement de seuil) soient proches : [[File:Inc290.bmp|110px]] (ou pour un dépassement de seuil : [[File:Inc291.bmp|170px]] | * a. Les n prévisions sont séparées en m groupes tels que chaque sous-groupe j contient les prévisions dont les probabilités de A (du non dépassement de seuil) soient proches : [[File:Inc290.bmp|110px]] (ou pour un dépassement de seuil : [[File:Inc291.bmp|170px]] | ||
| Ligne 41 : | Ligne 41 : | ||
| − | + | == Détection d'un biais == | |
| − | L'examen du diagramme de fiabilité peut également permettre de détecter la présence d'un biais systématique du système de prévision (fiche | + | L'examen du diagramme de fiabilité peut également permettre de détecter la présence d'un biais systématique du système de prévision ([[D.05_-_Absence_de_biais_systématique|fiche D.05]]). |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''Voir également''' | '''Voir également''' | ||
| − | Fiche | + | [[A.09_-_Quantiles_et_médiane|Fiche A.09 – Quantiles et médiane] |
| − | Fiche | + | [[D.02_-_Fiabilité_d'une_prévision|Fiche D.02 – Fiabilité d'une prévision]] |
| − | Fiche | + | [[D.05_-_Absence_de_biais_systématique|Fiche D.05 – Absence de biais]] |
| − | Fiche | + | [[D.08_-_Diagramme_de_Talagrand_(diagramme_de_rang)|Fiche D.08 – Diagramme de Talagrand]] |
| Ligne 66 : | Ligne 60 : | ||
* http://www.ecmwf.int/products/forecasts/guide/The_reliability_diagram.html | * http://www.ecmwf.int/products/forecasts/guide/The_reliability_diagram.html | ||
| − | http://www.metoffice.gov.uk/research/areas/seasonal-to-decadal/gpc-outlooks/user-guide/interpret-reliability | + | * http://www.metoffice.gov.uk/research/areas/seasonal-to-decadal/gpc-outlooks/user-guide/interpret-reliability |
*Laio, F. et Tamea, S. (2007). Verification tools for probabilistic forecasts of continuous hydrological variables. Hydrol. Earth Syst. Sc., 11: 1267–1277. | *Laio, F. et Tamea, S. (2007). Verification tools for probabilistic forecasts of continuous hydrological variables. Hydrol. Earth Syst. Sc., 11: 1267–1277. | ||
| + | |||
| + | ---------------------- | ||
| + | <references> | ||
[[Catégorie:Incertitudes]] | [[Catégorie:Incertitudes]] | ||
Version actuelle en date du 25 janvier 2015 à 15:00
Sommaire |
[modifier] Principe
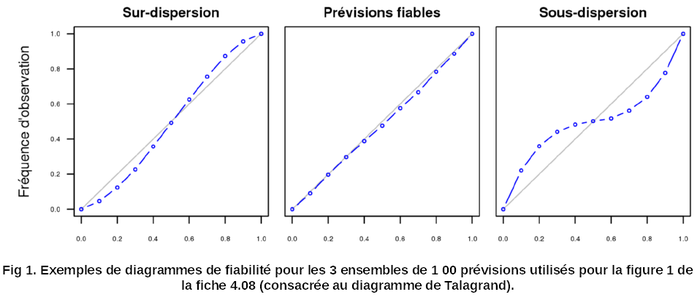
Le diagramme de fiabilité permet la même évaluation de la fiabilité d'un système de prévision que le diagramme de Talagrand (fiche D.08). Il permet la comparaison de la probabilité prévue d'un aléa (axe des abscisses) et de sa fréquence d'observation (axe des ordonnées). Un système de prévision fiable doit fournir des probabilités prévues proches des fréquences d'observation correspondantes : son diagramme de fiabilité sera donc proche de la bissectrice.
La suite de cette fiche présente deux manières pour construire le diagramme.
[modifier] Cas général : prévision d'une grandeur continue (diagramme PIT)
Le prévisionniste dispose d'une archive de n prévisions et des n observations correspondantes d'une variable X (de débit, de hauteur d'eau, de pluie, de température...). Chaque prévision est fournie sous la forme d'une densité de probabilité de la variable aléatoire X à prévoir ou d'un ensemble des valeurs de quelques quantiles (toujours les mêmes pour les n prévisions).
Le diagramme est construit point par point, chaque point correspondant à un quantile de prévision Qy(X) (y étant compris entre 0 et 1) :
- a. pour chaque prévision Xi (i étant compris entre 1 et n), l'observation est comparée au quantile de prévision qy (Xi) ;
- b. on calcule ainsi le nombre de prévisions telles que l'observation Xi est inférieur au quantile de prévision qy (Xi), qu'on note
;
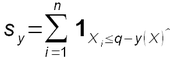- c. on en déduit la fréquence empirique d'observation du non dépassement de ce quantile fy = sy/n ;
- d. on reporte sur le graphe le point (y;fy).
Pour chaque prévision i, le quantile de prévision qy (Xi) est défini par le fait que la probabilité de non dépassement de cette valeur est égale à y : 
.
Si l'estimation Qy(X) du quantile est fiable alors la fréquence d'observation du non dépassement de cette valeurdoit être proche de y et donc le point doit être proche de la bissectrice[1].
Cette procédure est reproduite pour différents points (différents quantiles de prévision Qy(X)) pour obtenir le diagramme de fiabilité en reliant ces points (Fig.1, au verso).
[modifier] Variante : événements binaires et dépassements de seuil
Dans le cas où l'événement à prévoir ne peut prendre que deux valeurs A et B, comme un dépassement de seuil[2], le diagramme de fiabilité peut être construit ainsi :
- a. Les n prévisions sont séparées en m groupes tels que chaque sous-groupe j contient les prévisions dont les probabilités de A (du non dépassement de seuil) soient proches :
(ou pour un dépassement de seuil :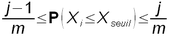 
- b. la fréquence fi des observations de l'alternative A (ou du non dépassement de seuil) est calculée pour chaque groupe j ;
- c. puis le point
est reporté sur le graphe.
Si les prévisions du groupe j sont fiables alors la fréquence d'observation fi doit être comprise entre (j-1)/m et j/m : le point reporté sera proche de la bissectrice.
[modifier] Détection d'un biais
L'examen du diagramme de fiabilité peut également permettre de détecter la présence d'un biais systématique du système de prévision (fiche D.05).
Voir également
[[A.09_-_Quantiles_et_médiane|Fiche A.09 – Quantiles et médiane]
Fiche D.02 – Fiabilité d'une prévision
Fiche D.08 – Diagramme de Talagrand
Pour aller plus loin
- http://www.ecmwf.int/products/forecasts/guide/The_reliability_diagram.html
- http://www.metoffice.gov.uk/research/areas/seasonal-to-decadal/gpc-outlooks/user-guide/interpret-reliability
- Laio, F. et Tamea, S. (2007). Verification tools for probabilistic forecasts of continuous hydrological variables. Hydrol. Earth Syst. Sc., 11: 1267–1277.
- ↑ Autrement dit, cela revient à compter sur l'ensemble des prévisions, combien d'observations ne dépassent pas le quantile de prévision Qy(X) – par exemple le quantile q10 % –, et à vérifier que l'on observe ce non dépassement à une fréquence proche de y (ici 10 %).
- ↑ Dans ce cas, la valeur A correspond au non dépassement de seuil et la valeur B au dépassement.
